Comprensione della modellizzazione della miscela di marketing bayesiano un’analisi approfondita delle specifiche precedenti.

Understanding Bayesian marketing mix modeling - in-depth analysis of previous specifications.

Esplorare la specifica del modello con LightweightMMM di Google

Il modello di marketing mix bayesiano sta ricevendo sempre più attenzione, soprattutto con i recenti rilasci di strumenti open source come LightweightMMM (Google) o PyMC Marketing (PyMC Labs). Sebbene questi framework semplifichino le complessità della modellizzazione bayesiana, è ancora cruciale che l’utente abbia una comprensione dei concetti bayesiani fondamentali e sia in grado di comprendere la specifica del modello.

In questo articolo, prendo LightweightMMM di Google come esempio pratico e mostro l’intuizione e il significato delle specifiche precedenti di questo framework. Dimostro la simulazione di campioni precedenti usando Python e la libreria scipy.

Dati

Utilizzo i dati resi disponibili da Robyn sotto licenza MIT.

Il dataset consiste in 208 settimane di ricavi (dal 23/11/2015 al 11/11/2019) con:

• Ricerca di similarità, Parte 5 Hashing Sensibile alla Località (LSH)
• Incontra MeLoDy Un Modello di Diffusione Testo-Audio Efficiente per la Sintesi Musicale.
• Come funziona la diagnosi medica dell’AI?

• 5 canali di spesa media: tv_S, ooh_S, print_S, facebook_S, search_S
• 2 canali media che hanno anche le informazioni sull’esposizione (Impression, Click): facebook_I, search_clicks_P
• Media organici senza spesa: newsletter
• Variabili di controllo: eventi, festività, vendite dei concorrenti (competitor_sales_B)

Specifiche del modello LightweightMMM

Le specifiche del modello LightweightMMM sono definite come segue:

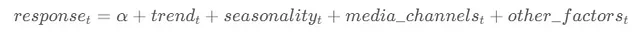
Questa specifica rappresenta un modello di regressione lineare additivo che spiega il valore di una risposta (variabile target) in un punto specifico nel tempo t.

Analizziamo ogni componente dell’equazione:

• α : Questo componente rappresenta l’intercetta o il valore di base della risposta. È il valore atteso della risposta quando tutti gli altri fattori sono zero.
• trend : Questo componente cattura la tendenza crescente o decrescente della risposta nel tempo.
• stagionalità : Questo componente rappresenta le fluttuazioni periodiche nella risposta.
• canali_media : Questo componente tiene conto dell’influenza dei canali media (tv, radio, annunci online) sulla risposta.
• altri_fattori : Questo componente comprende qualsiasi altra variabile che ha influenza sulla risposta, come il tempo, gli indicatori economici o le attività dei concorrenti.

Di seguito, analizzo ogni componente in dettaglio e spiego come interpretare le specifiche precedenti. Come promemoria, una distribuzione precedente è una distribuzione ipotizzata di alcuni parametri senza conoscenza dei dati sottostanti.

Intercetta

L’intercetta è definita seguendo una distribuzione seminormale con una deviazione standard di 2. Una distribuzione seminormale è una distribuzione di probabilità continua che assomiglia a una distribuzione normale, ma è limitata solo a valori positivi. La distribuzione è caratterizzata da un singolo parametro, la deviazione standard (scala). La distribuzione seminormale implica che l’intercetta può assumere solo valori positivi.

Il codice seguente genera campioni dalla distribuzione precedente dell’intercetta e visualizza la funzione di densità di probabilità (PDF) per una distribuzione seminormale con una scala di 2. Per visualizzazioni di altre componenti, fare riferimento al codice sorgente accompagnatorio nel repository Github.

from scipy import statsscale = 2halfnormal_dist = stats.halfnorm(scale=scale)samples = halfnormal_dist.rvs(size=1000)plt.figure(figsize=(20, 6))sns.histplot(samples, bins=50, kde=False, stat='density', alpha=0.5)sns.lineplot(x=np.linspace(0, 6, 100),       y=halfnormal_dist.pdf(np.linspace(0, 6, 100)), color='r')plt.title(f"Distribuzione seminormale con scala={scale}")plt.xlabel('x')plt.ylabel('P(X=x)')plt.show()

Tendenza

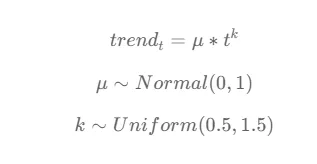
La tendenza viene definita come una relazione di legge di potenza tra il tempo t e il valore della tendenza. Il parametro μ rappresenta l’ampiezza o la magnitudine della tendenza, mentre k controlla la ripidezza o la curvatura della tendenza.

Il parametro μ è estratto da una distribuzione normale con media 0 e deviazione standard 1. Ciò implica che μ segue una distribuzione normale standard, centrata attorno a 0, con una deviazione standard di 1. La distribuzione normale consente valori positivi e negativi di μ, rappresentanti rispettivamente tendenze ascendenti o discendenti.

Il parametro k è estratto da una distribuzione uniforme tra 0,5 e 1,5. La distribuzione uniforme garantisce che k assuma valori che producano una curvatura ragionevole e significativa per la tendenza.

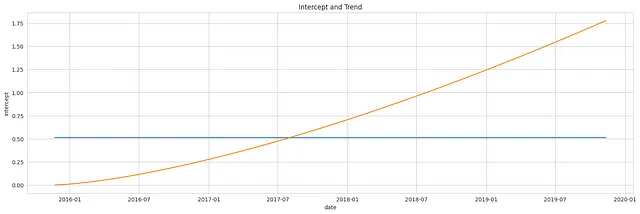
Il grafico qui sotto rappresenta i singoli componenti ottenuti dalle distribuzioni precedenti: un campione dell’intercetta e della tendenza, rappresentati singolarmente.

Stagionalità

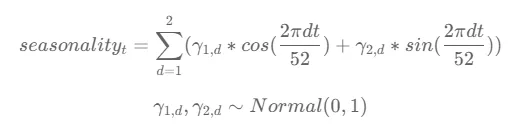
Ogni componente γ è estratto da una distribuzione normale con media 0 e deviazione standard 1.

Combinando le funzioni coseno e seno con diverse γ, possono essere modellati schemi ciclici per catturare la stagionalità presente nei dati. Le funzioni coseno e seno rappresentano il comportamento oscillante osservato nel periodo di 52 unità (settimane).

Il grafico qui sotto illustra un campione della stagionalità, intercetta e tendenza ottenuti dalle distribuzioni precedenti.

Altri fattori (variabili di controllo)

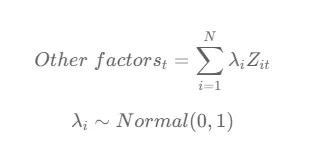
Ogni coefficiente di fattore λ ​​è estratto da una distribuzione normale con media 0 e deviazione standard 1, il che significa che λ può assumere valori positivi o negativi​, rappresentando la direzione e la magnitudine dell’influenza che ciascun fattore ha sul risultato.

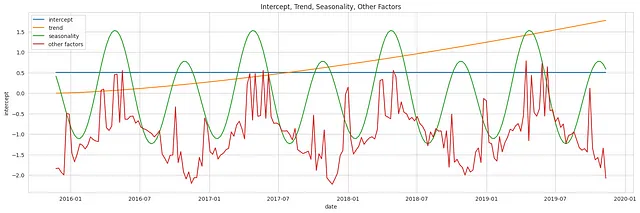
Il grafico qui sotto rappresenta i singoli componenti ottenuti dalle distribuzioni precedenti: un campione dell’intercetta, della tendenza, della stagionalità e delle variabili di controllo (vendite concorrenti B, newsletter, festività ed eventi), rappresentati singolarmente.

Canali Media

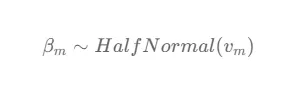
La distribuzione del coefficiente β di un canale media m è specificata come una distribuzione seminormale, dove il parametro di deviazione standard v è determinato dalla somma del costo totale associato al canale media m. Il costo totale riflette l’investimento o le risorse allocate a quel particolare canale media.

Trasformazioni dei media

In queste equazioni, stiamo modellando il comportamento dei canali media utilizzando una serie di trasformazioni, come adstock e saturazione di Hill.

Modellizzazione della miscela di marketing utilizzando PyMC3

Sperimentando con le priorità, la normalizzazione dei dati e confrontando la modellizzazione bayesiana con Robyn, l’MMM open-source di Facebook…

towardsdatascience.com

La variabile dei canali media rappresenta i canali media trasformati al tempo t. Si ottiene applicando una trasformazione al valore grezzo del canale media x. La trasformazione di Hill è controllata dai parametri K, un punto di semisaturazione (0 0).

La variabile x ∗ rappresenta il valore trasformato dei canali media al tempo t dopo aver subito la trasformazione di adstock. Viene calcolato aggiungendo il valore corrente del canale media grezzo al prodotto del valore trasformato precedente e del parametro di decadimento adstock λ.

I parametri K e S seguono distribuzioni gamma con parametri di forma e scala entrambi impostati a 1, mentre λ segue una distribuzione beta con parametri di forma 2 e 1.

La funzione di densità di probabilità dei parametri di saturazione di Hill K e S sono illustrati nel grafico qui sotto:

shape = 1scale = 1gamma_dist = stats.gamma(a=shape, scale=scale)samples = gamma_dist.rvs(size=1000)plt.figure(figsize=(20, 6))sns.histplot(samples, bins=50, kde=False, stat='density', alpha=0.5)sns.lineplot(x=np.linspace(0, 6, 100), y=gamma_dist.pdf(np.linspace(0, 6, 100)), color='r')plt.title(f"Distribuzione gamma per $K_m$ e $S_m$ con forma={shape} e scala={scale}")plt.xlabel('x')plt.ylabel('P(X=x)')# Mostra il graficoplt.show()python

La funzione di densità di probabilità del parametro di adstock λ è mostrata nel grafico qui sotto:

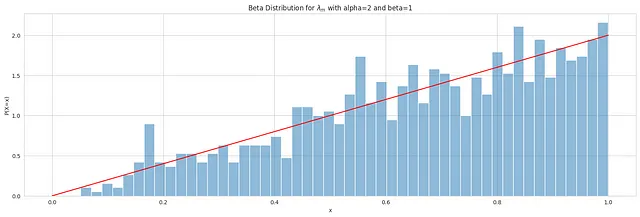
Una nota sulla specifica del parametro di adstock λ:

La funzione di densità di probabilità della distribuzione Beta(α = 2, β = 1) mostra un trend positivo, indicando che i valori più alti hanno una densità di probabilità maggiore. Nell’analisi dei media, diverse industrie e attività media possono mostrare diverse velocità di decadimento, con la maggior parte dei canali media che mostrano tipicamente piccole velocità di decadimento. Ad esempio, Robyn suggerisce i seguenti intervalli di decadimento λ per i comuni canali media: TV (0,3-0,8), OOH/Print/Radio (0,1-0,4) e digitale (0-0,3).

Nel contesto della distribuzione Beta(α = 2, β = 1), maggiori probabilità sono assegnate ai valori di λ più vicini a 1, mentre minori probabilità sono assegnate ai valori più vicini a 0. Di conseguenza, gli esiti o le osservazioni vicino alla fine superiore dell’intervallo [0,1] sono più probabili che si verifichino rispetto agli esiti vicino alla fine inferiore.

In alternativa, nei metodi bayesiani per la modellizzazione della miscela di media con effetti di trasporto e forma, il parametro di decadimento è definito come Beta(α = 3, β = 3), la cui funzione di densità di probabilità è illustrata di seguito. Questa distribuzione è simmetrica attorno a 0,5, indicando una probabilità uguale di osservare esiti ai due estremi e vicino al centro dell’intervallo [0,1].

Il grafico qui sotto rappresenta i singoli componenti ottenuti dalle distribuzioni precedenti: un campione dell’intercetta, della tendenza, della stagionalità, delle variabili di controllo e dei canali mediatici, rappresentati singolarmente.

Combinazione di tutti i componenti

Come accennato in precedenza, LightweightMMM modella una regressione lineare additiva combinando vari componenti come l’intercetta, la tendenza, la stagionalità, i canali mediatici e altri fattori campionati dalle loro distribuzioni precedenti per ottenere la risposta predittiva. Il grafico qui sotto visualizza la vera risposta e la risposta attesa campionata dalla distribuzione predittiva precedente.

Visualizzare un singolo campione rispetto al valore di risposta vero ci consente di osservare come la previsione del modello si confronta con l’esito effettivo per un insieme specifico di valori dei parametri. Può fornire una comprensione intuitiva di come il modello si comporta in quella particolare istanza.

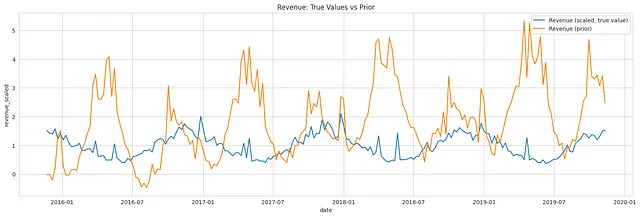
Controllo preventivo predittivo

Per ottenere insight più robusti, è generalmente consigliato campionare più volte dalla distribuzione predittiva precedente e misurare l’incertezza. Il controllo preventivo predittivo aiuta ad valutare l’adeguatezza del modello scelto e valutare se le previsioni del modello si allineano alle nostre aspettative, prima di osservare qualsiasi dato effettivo.

Il grafico qui sotto visualizza la distribuzione predittiva precedente mostrando il ricavo atteso (media) in ogni punto, insieme alle misure di incertezza. Possiamo vedere che il ricavo effettivo rientra nell’intervallo della deviazione standard, indicando che la specifica del modello è adatta per i dati osservati.

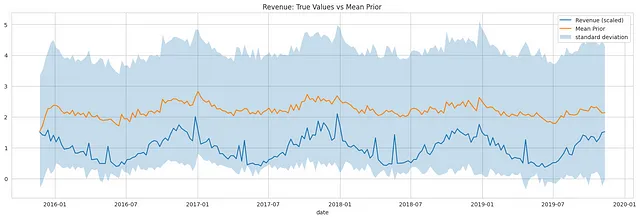
Conclusione

La modellazione della combinazione di marketing bayesiano può richiedere un tempo considerevole per essere padroneggiata. Spero che questo articolo ti abbia aiutato a migliorare la comprensione delle distribuzioni precedenti e delle specifiche del modello di marketing bayesiano.

Il codice completo può essere scaricato dal mio repo Github

Grazie per aver letto!