Immersione teorica profonda nella regressione lineare

Deep theoretical immersion in linear regression.

Scopri perché la regressione lineare è come è e come estenderla in modo naturale in vari modi

La maggior parte degli aspiranti blogger di data science lo fa: scrivono un articolo introduttivo sulla regressione lineare, ed è una scelta naturale poiché questo è uno dei primi modelli che impariamo quando entriamo nel campo. Mentre questi articoli sono ottimi per i principianti, la maggior parte non va abbastanza in profondità per soddisfare i data scientist senior.

Quindi, lasciami guidarti attraverso alcuni dettagli poco conosciuti, ma rinfrescanti, sulla regressione lineare che ti faranno diventare un miglior data scientist (e ti daranno punti bonus durante i colloqui di lavoro).

Questo articolo è piuttosto matematico, quindi per seguirlo è utile avere una solida conoscenza di probabilità e calcolo.

Il processo di generazione dei dati

Sono un grande fan di pensare al processo di generazione dei dati durante la modellizzazione. Le persone che hanno a che fare con la modellizzazione bayesiana sanno di cosa parlo, ma per gli altri: immagina di avere un dataset ( X , y ) composto da campioni ( x , y ). Dato x , come ottenere un target y ?

• DeepMind RoboCat Un modello di IA robotico auto-apprendente.
• Incontra BITE un nuovo metodo che ricostruisce la forma e le pose tridimensionali di un cane da un’immagine, anche con pose difficili come seduto e sdraiato.
• Altri Corsi Gratuiti sui Grandi Modelli Linguistici

Supponiamo di avere n punti dati e che ogni x abbia k componenti/caratteristiche.

Per un modello lineare con i parametri w ₁, …, wₖ (coefficients) , b (intercept) , σ (rumore) , l’assunzione è che il processo di generazione dei dati sia così:

1. Calcolare µ = w ₁ x ₁ + w ₂ x ₂ + … + wₖxₖ + b.
2. Tirare un y casuale ~ N ( µ, σ² ). Questo è indipendente dagli altri numeri generati casualmente. In alternativa: Tirare ε ~ N (0 , σ² ) e produrre y = µ + ε .

Ecco fatto. Queste due semplici righe sono equivalenti alle più importanti assunzioni della regressione lineare che le persone amano spiegare a lungo, ovvero linearità, omoschedasticità e indipendenza degli errori.

Dal passaggio 1. del processo, puoi anche vedere che modelliamo l’aspettativa µ con l’equazione lineare tipica w ₁ x ₁ + w ₂ x ₂ + … + wₖxₖ + b anziché il target effettivo. Sappiamo che non colpiremo comunque il target, quindi ci accontentiamo della media della distribuzione che genera y.

Estensioni

Modelli lineari generalizzati. Non siamo costretti a usare una distribuzione normale per il processo di generazione. Se ci occupiamo di un dataset che contiene solo target positivi , potrebbe essere utile assumere che una distribuzione di Poisson Poi( µ ) sia utilizzata invece di una distribuzione normale. Questo ti dà la regressione di Poisson.

Se il nostro dataset ha solo i target 0 e 1, usa una distribuzione di Bernoulli Ber( p ), dove p = sigmoid( µ ), et voilà: hai la regressione logistica.

Solo numeri tra 0, 1, …, n ? Usa una distribuzione binomiale per ottenere la regressione binomiale.

La lista continua. In poche parole:

Pensa a quale distribuzione potrebbe aver generato le etichette che osservi nei dati.

Cosa stiamo realmente minimizzando?

Ok, quindi abbiamo deciso su un modello ora. Come lo addestriamo? Come apprendiamo i parametri? Naturalmente, lo sai: abbiamo minimizzato l’errore quadratico (medio). Ma perché?

Il segreto è che si effettua una piana massima stima di verosimiglianza utilizzando il processo di generazione che abbiamo descritto prima. Le etichette che osserviamo sono y ₁, y ₂, …, yₙ , tutte generate indipendentemente tramite una distribuzione normale con medie µ ₁, µ ₂, …, µₙ. Qual è la verosimiglianza di vedere questi y? È:

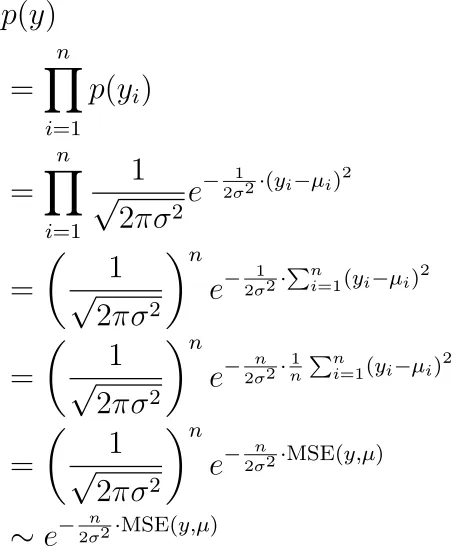
Ora vogliamo trovare i parametri (nascosti nei µᵢ ) per massimizzare questo termine. Ciò è equivalente a minimizzare l’errore quadratico medio, come si può vedere.

Estensioni

Varianze non uguali. Infatti, σ non deve essere costante. Puoi avere σᵢ diversi per ogni osservazione nel tuo dataset. In tal caso, si minimizza

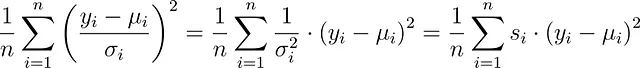
invece, che è minimi quadrati con pesi campione s. Le librerie di modellizzazione di solito ti consentono di impostare questi pesi. In scikit-learn, ad esempio, è possibile impostare la parola chiave sample_weight nella funzione fit.

In questo modo, puoi mettere maggiore enfasi su determinate osservazioni aumentando il corrispondente s. Ciò equivale a diminuire la varianza σ², vale a dire sei più sicuro che l’errore per questa osservazione sia più piccolo. Questo metodo è anche chiamato minimi quadrati pesati.

Varianze che dipendono dall’input. Puoi addirittura dire che la varianza dipende anche dall’input x. In questo caso, ottieni la funzione di perdita interessante che è anche chiamata attenuazione della varianza:

Tutto il processo di derivazione è descritto qui:

Ottieni stime di incertezza nei network neurali di regressione gratuitamente

Dato la giusta funzione di perdita, un normale neural network può produrre anche incertezza

towardsdatascience.com

Regolarizzazione. Invece di massimizzare solo la verosimiglianza delle etichette osservate y₁, y₂, …, yₙ, puoi prendere un punto di vista bayesiano e massimizzare la verosimiglianza a posteriori

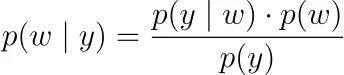
Qui, p(y|w) è la funzione di verosimiglianza di cui sopra. Dobbiamo decidere su una densità di probabilità per p(w), una cosiddetta prior o distribuzione a priori. Se diciamo che i parametri sono distribuiti normalmente in modo indipendente intorno a 0, cioè wᵢ ~ N(0, ν²), allora finiamo con regolarizzazione L2, vale a dire regressione di crinale. Per una distribuzione di Laplace, ripristiniamo la regolarizzazione L1, vale a dire LASSO.

Perché? Usiamo la distribuzione normale come esempio. Abbiamo

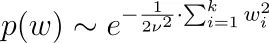
quindi insieme alla nostra formula per p(y|w) di cui sopra, dobbiamo massimizzare

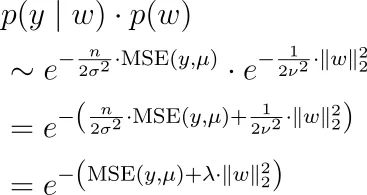
il che significa che dobbiamo minimizzare l’errore quadratico medio più un iperparametro di regolarizzazione volte la norma L2 di w.

Nota che abbiamo eliminato il denominatore p(y) dalla formula di Bayes poiché non dipende da w, quindi possiamo ignorarlo per l’ottimizzazione.

Puoi utilizzare qualsiasi altra distribuzione priore per i tuoi parametri per creare regolarizzazioni più interessanti. Puoi persino dire che i tuoi parametri w sono distribuiti normalmente ma correlati con qualche matrice di correlazione Σ.

Supponiamo che Σ sia definita positiva, ovvero siamo nel caso non degenere. In caso contrario, non esiste una densità p(w).

Se fai i calcoli, scoprirai che dovremmo quindi ottimizzare

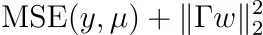
per qualche matrice Γ. Nota: Γ è invertibile e abbiamo Σ⁻¹ = ΓᵀΓ. Questo è anche chiamato regolarizzazione di Tikhonov.

Suggerimento: inizia con il fatto che

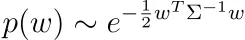
e ricorda che le matrici definite positive possono essere scomposte in un prodotto di una qualche matrice invertibile e la sua trasposta.

Minimizza La Funzione Di Perdita

Ottimo, quindi abbiamo definito il nostro modello e sappiamo cosa vogliamo ottimizzare. Ma come possiamo ottimizzarlo, ovvero imparare i migliori parametri che minimizzano la funzione di perdita? E quando c’è una soluzione unica? Scopriamolo.

Minimi Quadrati Ordinari

Supponiamo che non regolarizziamo e non usiamo pesi di campione. Allora, il MSE può essere scritto come

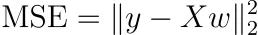
Questo è abbastanza astratto, quindi scriviamolo in modo diverso come

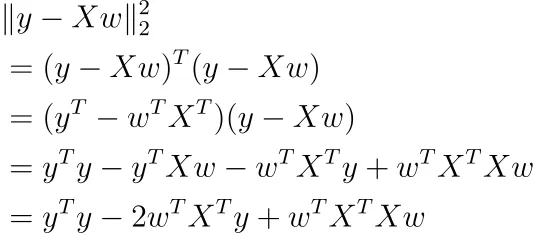
Utilizzando il calcolo matriciale, puoi derivare questa funzione rispetto a w (assumiamo che il termine di bias b sia incluso lì).

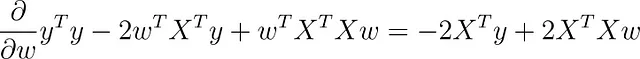
Se imposti questo gradiente a zero, finisci con

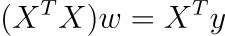
Se la matrice (n × k) X ha un rango di k, lo ha anche la matrice (k × k) X ᵀ X, ovvero è invertibile. Perché? Segue dal rango(X) = rango(X ᵀ X).

In questo caso, otteniamo la soluzione unica

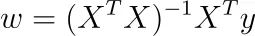
Nota: I pacchetti software non ottimizzano in questo modo, ma utilizzano invece la discesa del gradiente o altre tecniche iterative perché è più veloce. Tuttavia, la formula è bella e ci dà alcune intuizioni di alto livello sul problema.

Ma questo è davvero un minimo? Possiamo scoprirlo calcolando l’Hessiano, che è X ᵀ X. La matrice è semidefinita positiva poiché w ᵀ X ᵀ Xw = |Xw|² ≥ 0 per qualsiasi w. È addirittura strettamente definita positiva poiché X ᵀ X è invertibile, cioè 0 non è un autovettore, quindi il nostro w ottimale sta effettivamente minimizzando il nostro problema.

Multicollinearità perfetta

Questo era il caso favorevole. Ma cosa succede se X ha un rango inferiore a k? Questo potrebbe accadere se abbiamo due caratteristiche nel nostro set di dati in cui una è un multiplo dell’altra, ad esempio utilizziamo le caratteristiche altezza (in m) ed altezza (in cm) nel nostro set di dati. Quindi abbiamo altezza (in cm) = 100 * altezza (in m).

Può anche accadere se codifichiamo i dati categorici one-hot e non eliminiamo una delle colonne. Ad esempio, se abbiamo una caratteristica colore nel nostro set di dati che può essere rosso, verde o blu, allora possiamo codificare one-hot e ottenere tre colonne color_red, color_green e color_blue. Per queste caratteristiche, abbiamo color_red + color_green + color_blue = 1, che induce anche una multicollinearità perfetta.

In questi casi, il rango di X ᵀ X è anche inferiore a k, quindi questa matrice non è invertibile.

Fine della storia.

O no? In realtà, no, perché può significare due cose: ( X ᵀ X ) w = X ᵀ y ha

1. nessuna soluzione o
2. un numero infinito di soluzioni.

Risulta che nel nostro caso, possiamo ottenere una soluzione usando l’inverso di Moore-Penrose. Ciò significa che siamo nel caso di un numero infinito di soluzioni, tutte che ci danno la stessa perdita di errore quadratico medio (training).

Se denotiamo l’inverso di Moore-Penrose di A con A ⁺, possiamo risolvere il sistema di equazioni lineari come

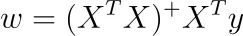
Per ottenere le altre soluzioni infinite, basta aggiungere lo spazio nullo di X ᵀ X a questa soluzione specifica.

Minimizzazione con regolarizzazione di Tikhonov

Ricordiamo che potevamo aggiungere una distribuzione a priori ai nostri pesi. Dovremmo quindi minimizzare

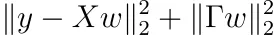
per qualche matrice invertibile Γ. Seguendo gli stessi passaggi della normale regressione lineare, cioè derivando rispetto a w e ponendo il risultato a zero, la soluzione è

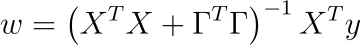
La parte bella:

XᵀX + ΓᵀΓ è sempre invertibile!

Scopriamo perché. È sufficiente mostrare che lo spazio nullo di X ᵀ X + ΓᵀΓ è solo {0}. Quindi, prendiamo un w con ( X ᵀ X + ΓᵀΓ) w = 0. Ora, il nostro obiettivo è mostrare che w = 0.

Dal momento che ( X ᵀ X + ΓᵀΓ) w = 0, ne segue che

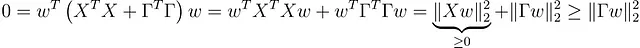
che a sua volta implica |Γ w | = 0 → Γ w = 0. Poiché Γ è invertibile, w deve essere 0. Usando lo stesso calcolo, possiamo vedere che l’Hessiano è anche definito positivo.

Bene, quindi la regolarizzazione di Tikhonov aiuta automaticamente a rendere unica la soluzione! Dal momento che la regressione ridge è un caso particolare della regressione di Tikhonov (per Γ = λ Iₖ, Iₖ è la matrice identità k-dimensionale), vale lo stesso.

Aggiunta di pesi campione

Come ultimo punto, aggiungiamo anche pesi campione alla regolarizzazione di Tikhonov. L’aggiunta di pesi campione è equivalente alla minimizzazione di

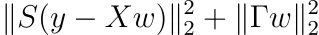
Per qualche matrice diagonale S con voci diagonali positive sᵢ. La minimizzazione è semplice come nel caso della normale regressione lineare. Il risultato è

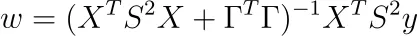
Nota: L’Hessiano è anche definito positivo.

Compiti per te

Supponiamo che per la regolarizzazione di Tikhonov, non imponiamo che i pesi debbano essere centrati attorno allo 0, ma attorno ad un altro punto w ₀. Mostra che il problema di ottimizzazione diventa

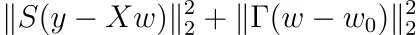
e che la soluzione è

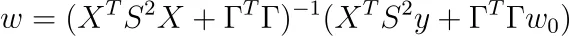
Questa è la forma più generale della regolarizzazione di Tikhonov. Alcune persone preferiscono definire P := S ², Q := ΓᵀΓ, come fatto qui .

Conclusione

In questo articolo, ti ho portato in un viaggio attraverso diversi aspetti avanzati della regressione lineare. Adottando una visione generativa, abbiamo potuto vedere che i modelli lineari generalizzati differiscono solo dai modelli lineari normali nel tipo di distribuzione che viene utilizzata per campionare il target y .

Poi abbiamo visto che minimizzare l’errore quadratico medio è equivalente a massimizzare la verosimiglianza dei valori osservati. Se imponiamo una precedente distribuzione normale sui parametri apprendibili, finiamo con la regolarizzazione di Tikhonov (e L2 come caso speciale). Possiamo utilizzare diverse distribuzioni precedenti come la distribuzione di Laplace, ma poi non ci sono più formule di soluzione chiuse. Tuttavia, gli approcci di programmazione convessa ti consentono anche di trovare i migliori parametri.

Come ultimo passo, abbiamo trovato molte formule di soluzione dirette per ciascun problema di minimizzazione considerato. Queste formule di soluzione di solito non vengono utilizzate in pratica per grandi set di dati, ma abbiamo potuto vedere che le soluzioni sono sempre univoche. E abbiamo anche imparato a fare un po’ di calcolo lungo il percorso. 😉

Spero che tu abbia imparato qualcosa di nuovo, interessante e prezioso oggi. Grazie per aver letto!

Come ultimo punto, se

1. vuoi sostenermi nella scrittura di altri articoli sul machine learning e
2. hai intenzione di abbonarti a Nisoo comunque,

perché non farlo tramite questo link ? Questo mi aiuterebbe molto! 😊

Per essere trasparenti, il prezzo per te non cambia, ma circa la metà delle tasse di abbonamento va direttamente a me.

Grazie mille se consideri di sostenermi!

Se hai domande, scrivimi su LinkedIn !