Cointegrazione vs Correlazione spuria Comprendere la differenza per un’analisi accurata

Cointegrazione vs correlazione spuria comprendere la differenza per un'analisi accurata

Perché la correlazione non implica la causalità per le serie temporali

Background

Nell’analisi delle serie temporali, è importante capire se una serie influisce su un’altra. Ad esempio, è utile per i trader di materie prime sapere se un aumento della materia prima A porta ad un aumento della materia prima B. Inizialmente, questa relazione veniva misurata utilizzando la regressione lineare, tuttavia, negli anni ’80 Clive Granger e Paul Newbold hanno dimostrato che questo approccio fornisce risultati errati, in particolare per le serie temporali non stazionarie. Di conseguenza, hanno concepito il concetto di cointegrazione, che ha valso a Granger un premio Nobel. In questo post, voglio discutere la necessità e l’applicazione della cointegrazione e perché è un concetto importante che i Data Scientist dovrebbero comprendere.

Correlazione spuria

Panoramica

Prima di discutere della cointegrazione, parliamo della sua necessità. Storicamente, statistici ed economisti utilizzavano la regressione lineare per determinare la relazione tra diverse serie temporali. Tuttavia, Granger e Newbold hanno dimostrato che questo approccio è errato e porta a qualcosa chiamato correlazione spuria.

Una correlazione spuria si verifica quando due serie temporali sembrano correlate ma in realtà mancano di una relazione causale. È l’aspetto classico dell’affermazione “la correlazione non implica la causalità”. È pericoloso perché anche i test statistici possono affermare che esiste una relazione causale.

Esempio

Un esempio di una relazione spuria è mostrato nei grafici seguenti:

• Risolvere il problema più grande di SimCLR – Spiegazione del paper BYOL
• Esplora il potere delle immagini dinamiche con Text2Cinemagraph un nuovo strumento di intelligenza artificiale per la generazione di cinemagraph da prompt di testo
• Introduzione pratica ai modelli Transformer BERT

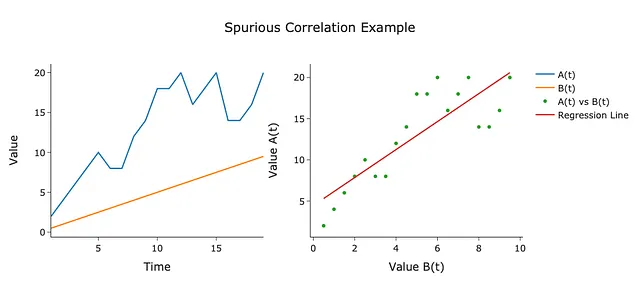
Qui abbiamo due serie temporali A(t) e B(t) rappresentate come funzione del tempo (sinistra) e rappresentate una contro l’altra (destra). Nota dal grafico a destra che c’è una certa correlazione tra le serie come indicato dalla linea di regressione. Tuttavia, osservando il grafico a sinistra, vediamo che questa correlazione è spuria perché B(t) aumenta costantemente mentre A(t) fluttua erraticamente. Inoltre, la distanza media tra le due serie temporali sta aumentando…