ANOVA bidirezionale in R

Bidirectional ANOVA in R.

Impara come fare una two-way ANOVA in R. Imparerai anche il suo obiettivo, le ipotesi, le assunzioni e come interpretare i risultati.

Introduzione

La two-way ANOVA (analisi della varianza) è un metodo statistico che consente di valutare l’effetto simultaneo di due variabili categoriche su una variabile continua quantitativa .

La two-way ANOVA è un’estensione della one-way ANOVA poiché consente di valutare gli effetti su una risposta numerica di due variabili categoriche invece di una. Il vantaggio di una two-way ANOVA rispetto a una one-way ANOVA è che testiamo la relazione tra due variabili, tenendo conto dell’effetto di una terza variabile. Inoltre, consente anche di includere la possibile interazione delle due variabili categoriche sulla risposta.

Il vantaggio di una two-way ANOVA rispetto a una one-way ANOVA è abbastanza simile al vantaggio di una correlazione rispetto a una regressione lineare multipla:

• La correlazione misura la relazione tra due variabili quantitative. La regressione lineare multipla misura anche la relazione tra due variabili, ma questa volta tenendo conto del potenziale effetto di altre covariate.
• La one-way ANOVA testa se una variabile quantitativa è diversa tra i gruppi. La two-way ANOVA testa anche se una variabile quantitativa è diversa tra i gruppi, ma questa volta tenendo conto dell’effetto di un’altra variabile qualitativa.

In precedenza, abbiamo discusso della one-way ANOVA in R. Ora mostriamo quando, perché e come eseguire una two-way ANOVA in R.

• Comprendere le leggi sulla proprietà intellettuale nell’algorithmic trading e nell’AI in finanza.
• Rapporto McKinsey Cosa significa per le vendite B2B?
• Una guida completa sui prezzi, i piani e i vantaggi di Insightly Marketing.

Prima di procedere, vorrei menzionare e descrivere brevemente alcuni metodi e test statistici correlati al fine di evitare eventuali confusioni:

Un test t di Student viene utilizzato per valutare l’effetto di una variabile categorica su una variabile continua quantitativa, quando la variabile categorica ha esattamente 2 livelli:

• Test t di Student per campioni indipendenti se le osservazioni sono indipendenti (ad esempio: se confrontiamo l’età tra donne e uomini)
• Test t di Student per campioni appaiati se le osservazioni sono dipendenti, cioè quando sono appaiate (è il caso in cui gli stessi soggetti sono misurati due volte, in due momenti diversi nel tempo, prima e dopo un trattamento ad esempio)

Per valutare l’effetto di una variabile categorica su una variabile quantitativa, quando la variabile categorica ha 3 o più livelli:

• ANOVA a una via (spesso indicata semplicemente come ANOVA) se i gruppi sono indipendenti (ad esempio un gruppo di pazienti che hanno ricevuto il trattamento A, un altro gruppo di pazienti che hanno ricevuto il trattamento B e l’ultimo gruppo di pazienti che non ha ricevuto alcun trattamento o un placebo)
• ANOVA a misura ripetuta se i gruppi sono dipendenti (quando gli stessi soggetti sono misurati tre volte, in tre momenti diversi nel tempo, prima, durante e dopo un trattamento ad esempio)

Una two-way ANOVA viene utilizzata per valutare gli effetti di 2 variabili categoriche (e la loro potenziale interazione) su una variabile continua quantitativa. Questo è l’argomento del post.

La regressione lineare viene utilizzata per valutare la relazione tra una variabile dipendente continua quantitativa e una o più variabili indipendenti:

• Regressione lineare semplice se c’è solo una variabile indipendente (che può essere quantitativa o qualitativa)
• Regressione lineare multipla se ci sono almeno due variabili indipendenti (che possono essere quantitative, qualitative o una combinazione di entrambe)

Un ANCOVA (analisi della covarianza) viene utilizzato per valutare l’effetto di una variabile categorica su una variabile quantitativa, mentre si controlla l’effetto di un’altra variabile quantitativa (nota come covariata). L’ANCOVA è in realtà un caso speciale di regressione lineare multipla con una combinazione di una variabile indipendente qualitativa e una quantitativa.

In questo post, iniziamo spiegando quando e perché una two-way ANOVA è utile, quindi facciamo alcune analisi descrittive preliminari e presentiamo come condurre una two-way ANOVA in R. Infine, mostriamo come interpretare e visualizzare i risultati. Menzioniamo e illustreremo brevemente anche come verificare le assunzioni sottostanti.

Dati

Per illustrare come effettuare una ANOVA bidirezionale in R, utilizzeremo il dataset penguins, disponibile dal pacchetto {palmerpenguins}.

Non abbiamo bisogno di importare il dataset, ma è necessario caricare prima il pacchetto e poi richiamare il dataset:

# install.packages("palmerpenguins")library(palmerpenguins)

dat <- penguins # rinomina il datasetstr(dat) # struttura del dataset

## tibble [344 × 8] (S3: tbl_df/tbl/data.frame)##  $ species          : Factor w/ 3 levels "Adelie","Chinstrap",..: 1 1 1 1 1 1 1 1 1 1 ...##  $ island           : Factor w/ 3 levels "Biscoe","Dream",..: 3 3 3 3 3 3 3 3 3 3 ...##  $ bill_length_mm   : num [1:344] 39.1 39.5 40.3 NA 36.7 39.3 38.9 39.2 34.1 42 ...##  $ bill_depth_mm    : num [1:344] 18.7 17.4 18 NA 19.3 20.6 17.8 19.6 18.1 20.2 ...##  $ flipper_length_mm: int [1:344] 181 186 195 NA 193 190 181 195 193 190 ...##  $ body_mass_g      : int [1:344] 3750 3800 3250 NA 3450 3650 3625 4675 3475 4250 ...##  $ sex              : Factor w/ 2 levels "female","male": 2 1 1 NA 1 2 1 2 NA NA ...##  $ year             : int [1:344] 2007 2007 2007 2007 2007 2007 2007 2007 2007 2007 ...

Il dataset contiene 8 variabili per 344 pinguini, riassunte di seguito:

summary(dat)

##       species          island    bill_length_mm  bill_depth_mm  ##  Adelie   :152   Biscoe   :168   Min.   :32.10   Min.   :13.10  ##  Chinstrap: 68   Dream    :124   1st Qu.:39.23   1st Qu.:15.60  ##  Gentoo   :124   Torgersen: 52   Median :44.45   Median :17.30  ##                                  Mean   :43.92   Mean   :17.15  ##                                  3rd Qu.:48.50   3rd Qu.:18.70  ##                                  Max.   :59.60   Max.   :21.50  ##                                  NA's   :2       NA's   :2      ##  flipper_length_mm  body_mass_g       sex           year     ##  Min.   :172.0     Min.   :2700   female:165   Min.   :2007  ##  1st Qu.:190.0     1st Qu.:3550   male  :168   1st Qu.:2007  ##  Median :197.0     Median :4050   NA's  : 11   Median :2008  ##  Mean   :200.9     Mean   :4202                Mean   :2008  ##  3rd Qu.:213.0     3rd Qu.:4750                3rd Qu.:2009  ##  Max.   :231.0     Max.   :6300                Max.   :2009  ##  NA's   :2         NA's   :2

In questo post, ci concentreremo sulle seguenti tre variabili:

• species: la specie del pinguino (Adelie, Chinstrap o Gentoo)
• sex: il sesso del pinguino (femmina e maschio)
• body_mass_g: la massa corporea del pinguino (in grammi)

Se necessario, maggiori informazioni su questo dataset possono essere trovate eseguendo ?penguins in R.

body_mass_g è la variabile continua quantitativa e sarà la variabile dipendente, mentre species e sex sono entrambe variabili qualitative.

Le ultime due variabili saranno le nostre variabili indipendenti, anche chiamate fattori. Assicurati che R le legga come fattori. Se non è il caso, dovranno essere trasformate in fattori.

Scopo e ipotesi di un’ANOVA a due vie

Come già accennato, un’ANOVA a due vie viene utilizzata per valutare contemporaneamente l’effetto di due variabili categoriali su una variabile continua quantitativa.

È chiamata ANOVA a due vie perché stiamo confrontando gruppi formati da due variabili categoriali indipendenti.

In questo caso, vogliamo sapere se la massa corporea dipende dalla specie e/o dal sesso. In particolare, ci interessa:

1. misurare e testare la relazione tra specie e massa corporea,
2. misurare e testare la relazione tra sesso e massa corporea e
3. eventualmente verificare se la relazione tra specie e massa corporea è diversa per le femmine e i maschi (che è equivalente a verificare se la relazione tra sesso e massa corporea dipende dalla specie)

Le prime due relazioni sono chiamate effetti principali, mentre il terzo punto è conosciuto come l’effetto di interazione.

Gli effetti principali testano se almeno un gruppo è diverso da un altro (controllando l’altra variabile indipendente). D’altra parte, l’effetto di interazione mira a testare se la relazione tra due variabili differisce a seconda del livello di una terza variabile.

Quando si esegue un’ANOVA a due vie, il test dell’effetto di interazione non è obbligatorio. Tuttavia, omettere un effetto di interazione può portare a conclusioni errate se l’effetto di interazione è presente.

Tornando all’esempio, abbiamo i seguenti test di ipotesi:

Effetto principale del sesso sulla massa corporea:

• H0: la massa corporea media è uguale tra femmine e maschi
• H1: la massa corporea media è diversa tra femmine e maschi

Effetto principale della specie sulla massa corporea:

• H0: la massa corporea media è uguale per tutte e 3 le specie
• H1: la massa corporea media è diversa per almeno una specie

Interazione tra sesso e specie:

• H0: non c’è interazione tra sesso e specie, il che significa che la relazione tra specie e massa corporea è la stessa per le femmine e i maschi (allo stesso modo, la relazione tra sesso e massa corporea è la stessa per tutte e 3 le specie)
• H1: c’è un’interazione tra sesso e specie, il che significa che la relazione tra specie e massa corporea è diversa per le femmine rispetto ai maschi (allo stesso modo, la relazione tra sesso e massa corporea dipende dalla specie)

Ipotesi di un’ANOVA a due vie

La maggior parte dei test statistici richiede alcune ipotesi affinché i risultati siano validi, e un’ANOVA a due vie non fa eccezione.

Le ipotesi di un’ANOVA a due vie sono simili a quelle di un’ANOVA a una via. Per riassumere:

• Tipo di variabile: la variabile dipendente deve essere continua quantitativa, mentre le due variabili indipendenti devono essere categoriali (con almeno due livelli).
• Indipendenza: le osservazioni dovrebbero essere indipendenti tra i gruppi e all’interno di ciascun gruppo.
• Normalità:
• Per campioni piccoli, i dati dovrebbero seguire approssimativamente una distribuzione normale
• Per campioni grandi (di solito n ≥ 30 in ogni gruppo/campione), la normalità non è richiesta (grazie al teorema del limite centrale)
• Uguaglianza delle varianze: le varianze dovrebbero essere uguali tra i gruppi.
• Outlier: non dovrebbero esserci outlier significativi in nessun gruppo.

Maggiori dettagli su queste ipotesi possono essere trovati nelle ipotesi di un’ANOVA a una via.

Ora che abbiamo visto le ipotesi sottostanti all’ANOVA a due vie, le esamineremo specificamente per il nostro dataset prima di applicare il test e interpretare i risultati.

Tipo di variabile

La variabile dipendente massa corporea è continua quantitativa, mentre entrambe le variabili indipendenti sesso e specie sono variabili qualitative (con almeno 2 livelli).

Quindi, questa ipotesi è soddisfatta.

Indipendenza

L’indipendenza viene di solito verificata in base alla progettazione dell’esperimento e al modo in cui i dati sono stati raccolti.

Per semplificare, le osservazioni sono di solito:

• indipendenti se ogni unità sperimentale (in questo caso un pinguino) è stata misurata solo una volta e le osservazioni sono state raccolte da una porzione rappresentativa e selezionata a caso della popolazione, o
• dipendenti se ogni unità sperimentale è stata misurata almeno due volte (come spesso accade nel campo medico ad esempio, con due misurazioni sugli stessi soggetti; una prima e una dopo il trattamento).

Nel nostro caso, la massa corporea è stata misurata solo una volta su ogni pinguino, e su un campione rappresentativo e casuale della popolazione, quindi l’assunzione di indipendenza è soddisfatta.

Normalità

Abbiamo un grande campione in tutti i sottogruppi (ogni combinazione dei livelli dei due fattori, chiamati cella):

table(dat$species, dat$sex)

##            ##             female male##   Adelie        73   73##   Chinstrap     34   34##   Gentoo        58   61

quindi la normalità non ha bisogno di essere verificata.

Per completezza, mostriamo comunque come verificare la normalità, come se avessimo campioni piccoli.

Ci sono diversi metodi per testare l’assunzione di normalità. I metodi più comuni sono:

• un grafico QQ per gruppo o sui residui, e/o
• un istogramma per gruppo o sui residui, e/o
• un test di normalità (ad esempio il test di Shapiro-Wilk) per gruppo o sui residui.

Il modo più semplice/breve è verificare la normalità con un grafico QQ sui residui. Per disegnare questo grafico, dobbiamo prima salvare il modello:

# salva il modellomod <- aov(body_mass_g ~ sex * species,  data = dat)

Questo pezzo di codice verrà spiegato più avanti.

Ora possiamo disegnare il grafico QQ sui residui. Mostriamo due modi per farlo, prima con la funzione plot() e poi con la funzione qqPlot() del pacchetto {car}:

# metodo 1plot(mod, which = 2)

# metodo 2library(car)

qqPlot(mod$residuals,  id = FALSE # rimuovi l'identificazione del punto)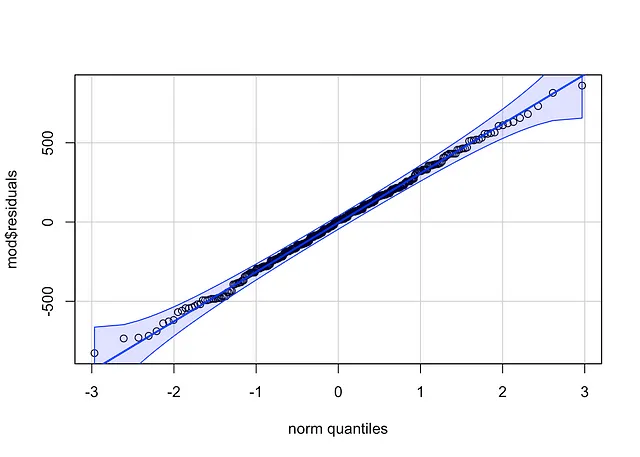

Il codice per il metodo 1 è leggermente più breve, ma manca l’intervallo di confidenza intorno alla linea di riferimento.

Se i punti seguono la linea retta (chiamata linea di Henry) e cadono all’interno della banda di confidenza, possiamo assumere la normalità. Questo è il caso qui.

Se preferisci verificare la normalità basandoti su un istogramma dei residui, ecco il codice:

# istogrammahist(mod$residuals)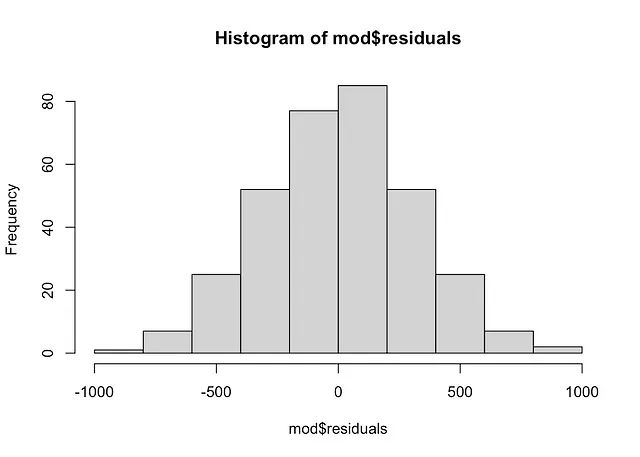

L’istogramma dei residui mostra una distribuzione gaussiana, che è in linea con la conclusione del grafico QQ.

Anche se il grafico QQ e l’istogramma sono ampiamente sufficienti per verificare la normalità, se desideri testarla in modo più formale con un test statistico, il test di Shapiro-Wilk può essere applicato anche sui residui:

# test di normalitàshapiro.test(mod$residuals)

## ##  Shapiro-Wilk normality test## ## data:  mod$residuals## W = 0.99776, p-value = 0.9367

⇒ Non rifiutiamo l’ipotesi nulla che i residui seguano una distribuzione normale (p-value = 0.937).

Dal grafico QQ-plot, dall’istogramma e dal test di Shapiro-Wilk, possiamo concludere che non rifiutiamo l’ipotesi nulla di normalità dei residui.

L’assunzione di normalità è quindi verificata, possiamo ora verificare l’uguaglianza delle varianze. 2

Omocefalicità delle varianze

L’uguaglianza delle varianze, anche chiamata omocefalicità delle varianze, può essere verificata visivamente con la funzione plot():

plot(mod, which = 3)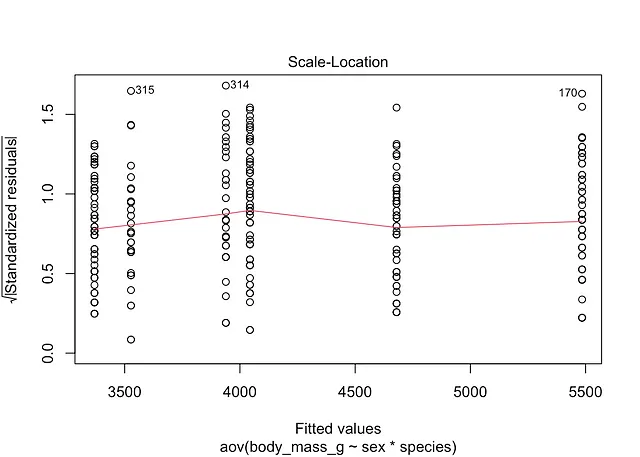

Dal momento che la dispersione dei residui è costante, la linea rossa liscia è orizzontale e piatta, sembra che l’assunzione di varianza costante sia soddisfatta qui.

Il grafico diagnostico sopra è sufficiente, ma se si preferisce può anche essere testato in modo più formale con il test di Levene (anche dal pacchetto {car}): 3

leveneTest(mod)

## Test di Levene per l'omocefalicità della varianza (centro = mediana)##        Df F value Pr(>F)## group   5  1.3908 0.2272##       327

⇒ Non rifiutiamo l’ipotesi nulla che le varianze siano uguali (valore p = 0,227).

Sia l’approccio visivo che quello formale danno la stessa conclusione; non rifiutiamo l’ipotesi di omocefalicità delle varianze.

Outliers

Il modo più semplice e comune per rilevare gli outliers è visivo grazie ai boxplot per gruppi.

Per femmine e maschi:

library(ggplot2)

# boxplot per sesso ggplot(dat) +  aes(x = sex, y = body_mass_g) +  geom_boxplot()

Per le tre specie:

# boxplot per specieggplot(dat) +  aes(x = species, y = body_mass_g) +  geom_boxplot()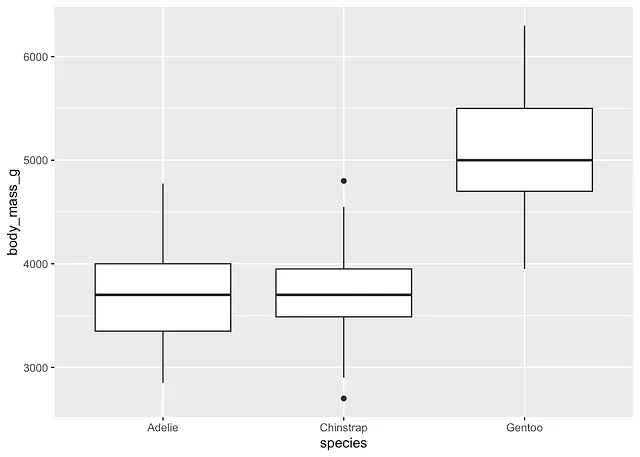

Ci sono, come definito dal criterio dell’intervallo interquartile, due outliers per la specie Chinstrap. Tuttavia, questi punti non sono abbastanza estremi da influenzare i risultati.

Pertanto, consideriamo che l’assunzione di nessun outlier significativo sia soddisfatta.

ANOVA a due vie

Aver verificato che tutte le assunzioni sono soddisfatte, ci consente di procedere con l’implementazione dell’ANOVA a due vie in R.

Ciò ci consentirà di rispondere alle seguenti domande di ricerca:

• Controllando la specie, la massa corporea è significativamente diversa tra i due sessi?
• Controllando il sesso, la massa corporea è significativamente diversa per almeno una specie?
• La relazione tra specie e massa corporea è diversa tra pinguini femmine e maschi?

Analisi preliminari

Prima di effettuare qualsiasi test statistico, è buona pratica effettuare alcune statistiche descrittive al fine di avere una prima panoramica dei dati e, forse, avere un’idea dei risultati attesi.

Ciò può essere fatto tramite statistiche descrittive o grafici.

Statistiche descrittive

Se vogliamo mantenerlo semplice, possiamo calcolare solo la media per ogni sottogruppo:

# media per gruppoaggregate(body_mass_g ~ species + sex,  data = dat,  FUN = mean)

##     species    sex body_mass_g## 1    Adelie female    3368.836## 2 Chinstrap female    3527.206## 3    Gentoo female    4679.741## 4    Adelie   male    4043.493## 5 Chinstrap   male    3938.971## 6    Gentoo   male    5484.836

O in alternativa, la media e la deviazione standard per ogni sottogruppo utilizzando il pacchetto {dplyr}:

# media e sd per gruppo
library(dplyr)

group_by(dat, sex, species) %>%  summarise(    mean = round(mean(body_mass_g, na.rm = TRUE)),    sd = round(sd(body_mass_g, na.rm = TRUE))  )

## # A tibble: 8 × 4## # Gruppi:   sex [3]##   sex    species    mean    sd##   <fct>  <fct>     <dbl> <dbl>## 1 female Adelie     3369   269## 2 female Chinstrap  3527   285## 3 female Gentoo     4680   282## 4 male   Adelie     4043   347## 5 male   Chinstrap  3939   362## 6 male   Gentoo     5485   313## 7 <NA>   Adelie     3540   477## 8 <NA>   Gentoo     4588   338

Grafici

Se sei un lettore frequente del blog, sai che mi piace disegnare grafici per visualizzare i dati a disposizione prima di interpretare i risultati di un test.

Il grafico più appropriato quando abbiamo una variabile quantitativa e due qualitative è un boxplot per gruppo. Questo può essere facilmente realizzato con il pacchetto {ggplot2}:

# boxplot per gruppo
library(ggplot2)

ggplot(dat) +  aes(x = species, y = body_mass_g, fill = sex) +  geom_boxplot()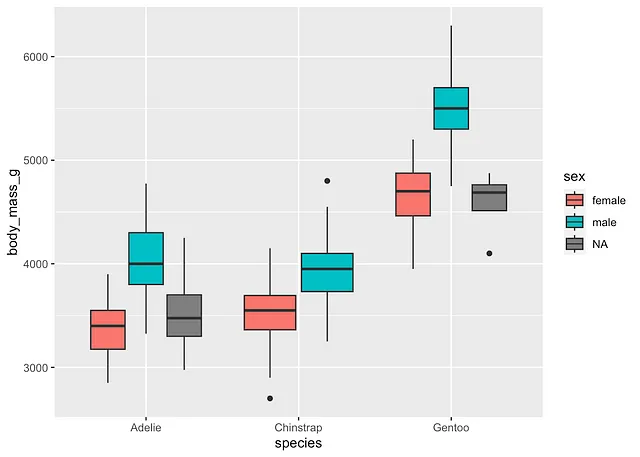

Alcune osservazioni sono mancanti per il sesso, possiamo rimuoverle per avere un grafico più conciso:

dat %>%  filter(!is.na(sex)) %>%  ggplot() +  aes(x = species, y = body_mass_g, fill = sex) +  geom_boxplot()

Nota che avremmo potuto anche realizzare il seguente grafico:

dat %>%  filter(!is.na(sex)) %>%  ggplot() +  aes(x = sex, y = body_mass_g, fill = species) +  geom_boxplot()

Ma per un grafico più leggibile, tendo a preferire mettere la variabile con il minor numero di livelli come colore (che è in realtà l’argomento fill nel livello aes()) e la variabile con il maggior numero di categorie sull’asse x (cioè l’argomento x nel livello aes()).

Dalle medie e dai boxplot per sottogruppo, possiamo già vedere che, nel nostro campione:

• le pinguine femmine tendono ad avere una massa corporea più bassa rispetto ai maschi, ed è il caso per tutte le specie considerate, e
• la massa corporea è maggiore per le pinguine Gentoo rispetto alle altre due specie.

Tieni presente che queste conclusioni sono valide solo all’interno del nostro campione! Per generalizzare queste conclusioni alla popolazione, dobbiamo eseguire la ANOVA a due vie e verificare la significatività delle variabili esplicative. Questo è l’obiettivo della prossima sezione.

ANOVA a due vie in R

Come anticipato in precedenza, includere un effetto di interazione in una ANOVA a due vie non è obbligatorio. Tuttavia, al fine di evitare conclusioni errate, si consiglia di verificare prima se l’interazione è significativa o meno e, a seconda dei risultati, includerla o meno.

Se l’interazione non è significativa, è sicuro rimuoverla dal modello finale. Al contrario, se l’interazione è significativa, dovrebbe essere inclusa nel modello finale che verrà utilizzato per interpretare i risultati.

Iniziamo quindi con un modello che include i due effetti principali (cioè sesso e specie) e l’interazione:

# ANOVA a due vie con interazione# salva il modello mod <- aov(body_mass_g ~ sex * species, data = dat)

# risultati di stampasommario(mod)

##              Df    Sum Sq  Mean Sq F value   Pr(>F)    ## sex           1  38878897 38878897 406.145  < 2e-16 ***## species       2 143401584 71700792 749.016  < 2e-16 ***## sex:species   2   1676557   838278   8.757 0.000197 ***## Residuals   327  31302628    95727                     ## ---## Codici significativi: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1## 11 osservazioni eliminate a causa di valori mancanti

La somma dei quadrati (colonna Sum Sq) mostra che la specie spiega una grande parte della variabilità della massa corporea. È il fattore più importante nell’explicare questa variabilità.

I valori p sono visualizzati nell’ultima colonna dell’output sopra ( Pr(>F) ). Da questi valori p, si conclude che, al livello di significatività del 5%:

• controllando la specie, la massa corporea è significativamente diversa tra i due sessi,
• controllando il sesso, la massa corporea è significativamente diversa per almeno una specie, e
• l’interazione tra sesso e specie (visualizzata alla linea sex:species nell’output sopra) è significativa.

Quindi, dall’effetto di interazione significativo, abbiamo appena visto che la relazione tra massa corporea e specie è diversa tra maschi e femmine. Poiché è significativo, dobbiamo mantenerlo nel modello e dovremmo interpretare i risultati da quel modello.

Se, al contrario, l’interazione non fosse significativa (cioè se il valore p ≥ 0,05), avremmo rimosso questo effetto di interazione dal modello. A scopo illustrativo, di seguito il codice per una ANOVA a due vie senza interazione, definita come modello additivo:

# ANOVA a due vie senza interazioneaov(body_mass_g ~ sex + species, data = dat)

Per i lettori abituati a eseguire regressioni lineari in R, si noterà che la struttura del codice per una ANOVA a due vie è in realtà simile:

• la formula è variabile dipendente ~ variabili indipendenti
• il segno + viene utilizzato per includere le variabili indipendenti senza interazione
• il segno * viene utilizzato per includere le variabili indipendenti con un’interazione

La somiglianza con una regressione lineare non è una sorpresa perché una ANOVA a due vie, come tutte le ANOVA, è in realtà un modello lineare.

Si noti che il seguente codice funziona anche e dà gli stessi risultati:

# metodo 2mod2 <- lm(body_mass_g ~ sex * species, data = dat)

Anova(mod2)

## Tabella ANOVA (test di tipo II)## ## Risposta: body_mass_g##                Sum Sq  Df F value    Pr(>F)    ## sex          37090262   1 387.460 < 2.2e-16 ***## species     143401584   2 749.016 < 2.2e-16 ***## sex:species   1676557   2   8.757 0.0001973 ***## Residuals    31302628 327                      ## ---## Codici significativi: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Si noti che la funzione aov() assume un disegno bilanciato , il che significa che abbiamo dimensioni campionarie uguali all’interno dei livelli delle nostre variabili di raggruppamento indipendenti.

Per un disegno non bilanciato, cioè numeri di soggetti non uguali in ogni sottogruppo, i metodi consigliati sono:

• la ANOVA di tipo II quando non c’è interazione significativa, che può essere fatta in R con Anova(mod, type = "II"), 5 e
• la ANOVA di tipo III quando c’è un’interazione significativa, che può essere fatta in R con Anova(mod, type = "III").

Questo va oltre lo scopo del post e assumiamo qui un disegno bilanciato. Per il lettore interessato, vedere questa discussione dettagliata sulla ANOVA di tipo I, tipo II e tipo III.

Confronti a coppie

Dai due principali effetti significativi abbiamo concluso che:

• controllando per la specie, la massa corporea è diversa tra femmine e maschi, e
• controllando per il sesso, la massa corporea è diversa per almeno una specie.

Se la massa corporea è diversa tra i due sessi, dato che ci sono esattamente due sessi, deve essere perché la massa corporea è significativamente diversa tra femmine e maschi.

Se si vuole sapere quale sesso ha la massa corporea più alta, si può dedurre dalle medie e/o dai boxplot per sottogruppo. Qui, è chiaro che i maschi hanno una massa corporea significativamente più alta delle femmine.

Tuttavia, non è così semplice per la specie. Spiego perché non è facile come per i sessi.

Ci sono tre specie (Adelie, Chinstrap e Gentoo), quindi ci sono 3 coppie di specie:

1. Adelie e Chinstrap
2. Adelie e Gentoo
3. Chinstrap e Gentoo

Se la massa corporea è significativamente diversa per almeno una specie, potrebbe essere che:

• la massa corporea è significativamente diversa tra Adelie e Chinstrap ma non significativamente diversa tra Adelie e Gentoo, e non significativamente diversa tra Chinstrap e Gentoo, o
• la massa corporea è significativamente diversa tra Adelie e Gentoo ma non significativamente diversa tra Adelie e Chinstrap, e non significativamente diversa tra Chinstrap e Gentoo, o
• la massa corporea è significativamente diversa tra Chinstrap e Gentoo ma non significativamente diversa tra Adelie e Chinstrap, e non significativamente diversa tra Adelie e Gentoo.

Oppure, potrebbe anche essere che:

• la massa corporea è significativamente diversa tra Adelie e Chinstrap e tra Adelie e Gentoo, ma non significativamente diversa tra Chinstrap e Gentoo, o
• la massa corporea è significativamente diversa tra Adelie e Chinstrap e tra Chinstrap e Gentoo, ma non significativamente diversa tra Adelie e Gentoo, o
• la massa corporea è significativamente diversa tra Chinstrap e Gentoo e tra Adelie e Gentoo, ma non significativamente diversa tra Adelie e Chinstrap.

Infine, potrebbe anche essere che la massa corporea sia significativamente diversa tra tutte le specie.

Come per una ANOVA a singolo fattore, non possiamo, in questa fase, sapere con precisione quale specie è diversa da quale in termini di massa corporea. Per saperlo, dobbiamo confrontare ogni specie due a due grazie a test post-hoc (anche noti come confronti a coppie).

Ci sono diversi test post-hoc, il più comune è il Tukey HSD, che testa tutte le possibili coppie di gruppi. Come accennato in precedenza, questo test deve essere effettuato solo sulla variabile specie perché ci sono solo due livelli per il sesso.

Come per la ANOVA a singolo fattore, il Tukey HSD può essere fatto in R come segue:

# metodo 1TukeyHSD(mod, which = "species")

##   Tukey multiple comparisons of means##     95% family-wise confidence level## ## Fit: aov(formula = body_mass_g ~ sex * species, data = dat)## ## $species##                        diff       lwr       upr     p adj## Chinstrap-Adelie   26.92385  -80.0258  133.8735 0.8241288## Gentoo-Adelie    1377.65816 1287.6926 1467.6237 0.0000000## Gentoo-Chinstrap 1350.73431 1239.9964 1461.4722 0.0000000

oppure utilizzando il pacchetto {multcomp}:

# metodo 2library(multcomp)

summary(glht(  aov(body_mass_g ~ sex + species,    data = dat  ),  linfct = mcp(species = "Tukey")))

## ##   Test simultanei per ipotesi lineari generali## ## Comparazioni multiple di medie: Contrasti di Tukey## ## ## Adattamento: aov(formula = body_mass_g ~ sex + species, data = dat)## Ipotesi lineari:##                         Stima Errore standard t value Pr(>|t|)    ## Chinstrap - Adelie == 0    26,92      46,48   0,579     0,83    ## Gentoo - Adelie == 0     1377,86      39,10  35,236   <1e-05 ***## Gentoo - Chinstrap == 0  1350,93      48,13  28,067   <1e-05 ***## ---## Codice di significatività:  0 '***' 0,001 '**' 0,01 '*' 0,05 '.' 0,1 ' ' 1## (Valori p corretti riportati -- metodo a passo singolo)

oppure utilizzando la funzione pairwise.t.test() con il metodo di correzione del valore p di tua scelta:

# metodo 3pairwise.t.test(dat$body_mass_g, dat$species,  p.adjust.method = "BH")

## ## Confronti a coppie tramite test t con SD combinata ## ## dati:  dat$body_mass_g e dat$species ## ##           Adelie Chinstrap## Chinstrap 0,63  -        ## Gentoo    <2e-16 <2e-16   ## ## Metodo di correzione del valore p: BH

Nota che quando si utilizza il secondo metodo, è il modello senza interazione che deve essere specificato nella funzione glht(), anche se l’interazione è significativa. Inoltre, non dimenticare di sostituire mod e species nel mio codice con il nome del tuo modello e il nome della tua variabile indipendente.

Entrambi i metodi danno gli stessi risultati, ovvero:

• la massa corporea non è significativamente diversa tra Chinstrap e Adelie (valore p corretto = 0,83),
• la massa corporea è significativamente diversa tra Gentoo e Adelie (valore p corretto < 0,001), e
• la massa corporea è significativamente diversa tra Gentoo e Chinstrap (valore p corretto < 0,001).

Ricorda che sono riportati i valori p corretti, per prevenire il problema del test multiplo che si verifica quando si confrontano diverse coppie di gruppi.

Se desideri confrontare tutte le combinazioni di gruppi, è possibile farlo con la funzione TukeyHSD() specificando l’interazione nell’argomento which:

# tutte le combinazioni di sesso e specieTukeyHSD(mod,  which = "sex:species")

##   Confronti multipli di Tukey per le media##     Intervallo di confidenza al 95%## ## Adattamento: aov(formula = body_mass_g ~ sex * species, data = dat)## ## $`sex:species`##                                      diff       lwr       upr     p adj## male:Adelie-female:Adelie        674,6575  527,8486  821,4664 0,0000000## female:Chinstrap-female:Adelie   158,3703  -25,7874  342,5279 0,1376213## male:Chinstrap-female:Adelie     570,1350  385,9773  754,2926 0,0000000## female:Gentoo-female:Adelie     1310,9058 1154,8934 1466,9181 0,0000000## male:Gentoo-female:Adelie       2116,0004 1962,1408 2269,8601 0,0000000## female:Chinstrap-male:Adelie    -516,2873 -700,4449 -332,1296 0,0000000## male:Chinstrap-male:Adelie      -104,5226 -288,6802   79,6351 0,5812048## female:Gentoo-male:Adelie        636,2482  480,2359  792,2606 0,0000000## male:Gentoo-male:Adelie         1441,3429 1287,4832 1595,2026 0,0000000## male:Chinstrap-female:Chinstrap  411,7647  196,6479  626,8815 0,0000012## female:Gentoo-female:Chinstrap  1152,5355  960,9603 1344,1107 0,0000000## male:Gentoo-female:Chinstrap    1957,6302 1767,8040 2147,4564 0,0000000## female:Gentoo-male:Chinstrap     740,7708  549,1956  932,3460 0,0000000## male:Gentoo-male:Chinstrap      1545,8655 1356,0392 1735,6917 0,0000000## male:Gentoo-female:Gentoo        805,0947  642,4300  967,7594 0,0000000

O con la funzione HSD.test() del pacchetto {agricolae}, che indica i sottogruppi che non differiscono significativamente tra loro con la stessa lettera:

library(agricolae)

HSD.test(mod,  trt = c("sex", "species"),  console = TRUE # stampa i risultati)

## ## Studio: mod ~ c("sex", "species")## ## Test HSD per body_mass_g ## ## Media dell'errore quadratico:  95726.69 ## ## sex:species,  medie## ##                  body_mass_g      std  r  Min  Max## female:Adelie       3368.836 269.3801 73 2850 3900## female:Chinstrap    3527.206 285.3339 34 2700 4150## female:Gentoo       4679.741 281.5783 58 3950 5200## male:Adelie         4043.493 346.8116 73 3325 4775## male:Chinstrap      3938.971 362.1376 34 3250 4800## male:Gentoo         5484.836 313.1586 61 4750 6300## ## Alpha: 0.05 ; DF dell'errore: 327 ## Valore critico del range studentizzato: 4.054126 ## ## I gruppi in base alla probabilità di differenze tra le medie e il livello alfa (0,05)## ## I trattamenti con la stessa lettera non differiscono significativamente.## ##                  body_mass_g gruppi## male:Gentoo         5484.836      a## female:Gentoo       4679.741      b## male:Adelie         4043.493      c## male:Chinstrap      3938.971      c## female:Chinstrap    3527.206      d## female:Adelie       3368.836      d

Se hai molti gruppi da confrontare, potrebbe essere più facile interpretarli rappresentandoli graficamente:

# imposta i margini degli assi in modo che le etichette non vengano tagliatepar(mar = c(4.1, 13.5, 4.1, 2.1))

# crea l'intervallo di confidenza per ogni confrontoplot(TukeyHSD(mod, which = "sex:species"),  las = 2 # ruota le etichette dell'asse x)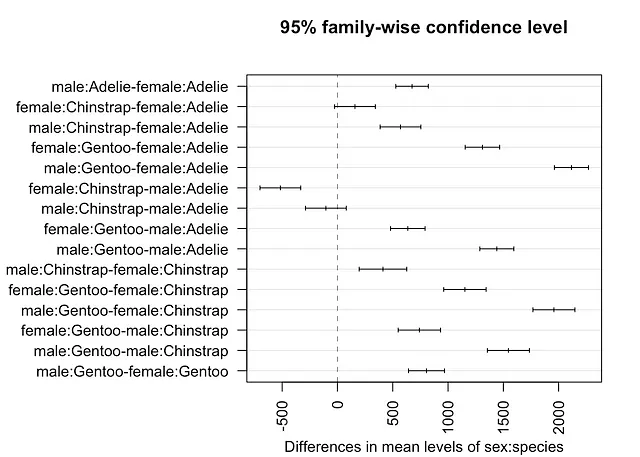

Dai risultati e dal grafico sopra, si può concludere che tutte le combinazioni di sesso e specie sono significativamente diverse, tranne tra Chinstrap femmina e Adelie femmina (valore p = 0,138) e Chinstrap maschio e Adelie maschio (valore p = 0,581).

Questi risultati, che peraltro sono in linea con i boxplot mostrati in precedenza e che saranno confermati con le visualizzazioni seguenti, concludono l’ANOVA a due vie in R.

Visualizzazioni

Se si desidera visualizzare i risultati in modo diverso da quanto già presentato nelle analisi preliminari, di seguito sono riportate alcune idee di grafici utili.

Prima di tutto, con la media e l’errore standard della media per sottogruppo utilizzando la funzione allEffects() del pacchetto {effects}:

# metodo 1library(effects)

plot(allEffects(mod))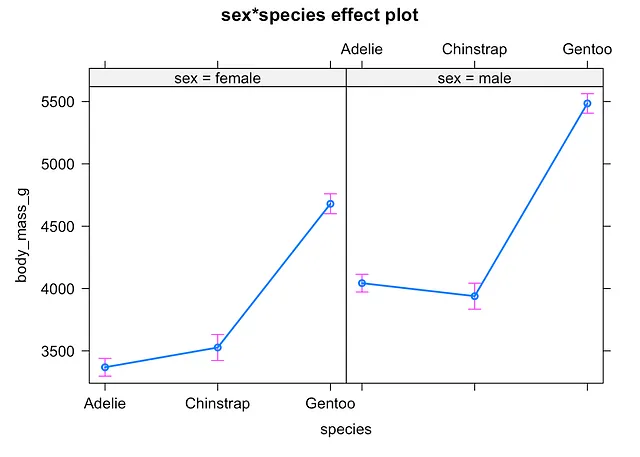

O utilizzando il pacchetto {ggpubr}:

# metodo 2library(ggpubr)

ggline(subset(dat, !is.na(sex)), # rimuove il livello NA per il sesso  x = "species",  y = "body_mass_g",  color = "sex",  add = c("mean_se") # aggiunge media e errore standard) +  labs(y = "Media del peso corporeo (g)")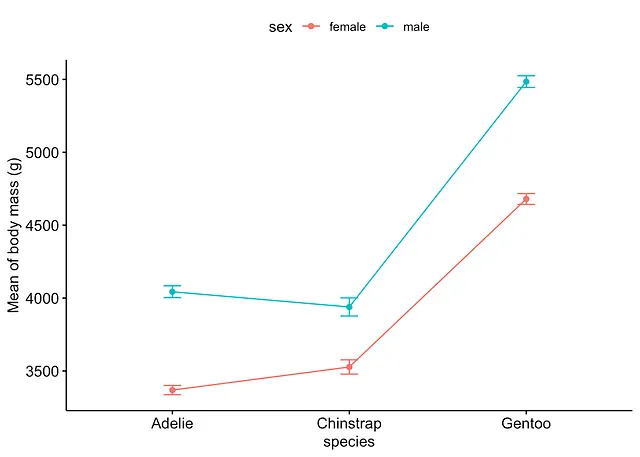

In alternativa, utilizzando {Rmisc} e {ggplot2} :

library(Rmisc)

# calcola la media e l'errore standard della media per sottogruppi
summary_stat <- summarySE(dat,  measurevar = "body_mass_g",  groupvars = c("species", "sex"))

# grafico della media e dell'errore standard della media
ggplot(  subset(summary_stat, !is.na(sex)), # rimuovi il livello NA per il sesso
        aes(x = species, y = body_mass_g, colour = sex)) +  
  geom_errorbar(aes(ymin = body_mass_g - se, ymax = body_mass_g + se), # aggiungi le barre di errore
                width = 0.1 # larghezza delle barre di errore
                ) +  
  geom_point() +  
  labs(y = "Media della massa corporea (g)")

In secondo luogo, se preferisci disegnare solo la media per sottogruppo:

with(  dat,  interaction.plot(species, sex, body_mass_g))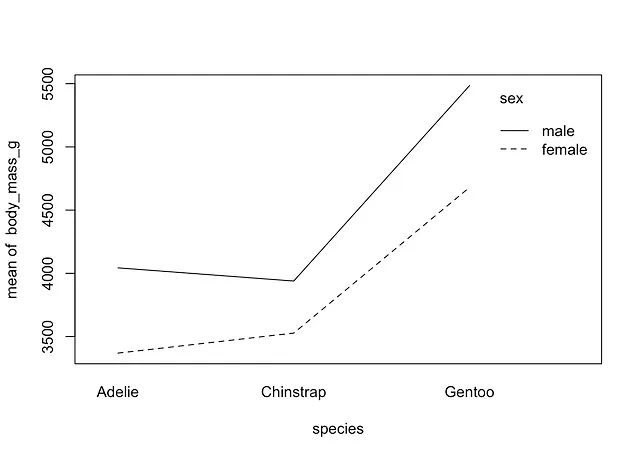

Infine, per coloro che sono familiari con GraphPad, è probabile che siano familiari con la rappresentazione grafica della media e delle barre di errore come segue:

# grafico della media e dell'errore standard della media come barplot
ggplot(  subset(summary_stat, !is.na(sex)), # rimuovi il livello NA per il sesso
        aes(x = species, y = body_mass_g, fill = sex)) +  
  geom_bar(position = position_dodge(), stat = "identity") +  
  geom_errorbar(aes(ymin = body_mass_g - se, ymax = body_mass_g + se), # aggiungi le barre di errore
                width = 0.25, # larghezza delle barre di errore
                position = position_dodge(.9)  ) +  
  labs(y = "Media della massa corporea (g)")

Conclusioni

In questo post, abbiamo iniziato con alcuni promemoria sui diversi test che esistono per confrontare una variabile quantitativa tra gruppi. Ci siamo poi concentrati sul test ANOVA a due vie, partendo dal suo obiettivo e dalle ipotesi fino alla sua implementazione in R, insieme alle interpretazioni e ad alcune visualizzazioni. Abbiamo anche accennato brevemente alle sue presunzioni sottostanti e ad un test post-hoc per confrontare tutti i sottogruppi.

Tutto ciò è stato illustrato con il dataset penguins disponibile dal pacchetto {palmerpenguins}.

Grazie per la lettura.

Spero che questo articolo ti aiuti a condurre un ANOVA a due vie con i tuoi dati.

Come sempre, se hai una domanda o un suggerimento relativo all’argomento trattato in questo articolo, aggiungilo come commento in modo che altri lettori possano beneficiare della discussione.

1. In teoria, un’ANOVA a una via può essere utilizzata anche per confrontare 2 gruppi, e non solo 3 o più. Tuttavia, nella pratica, spesso si effettua un test t di Student per confrontare 2 gruppi, e un’ANOVA a una via per confrontare 3 o più gruppi. Le conclusioni ottenute tramite un test t di Student per campioni indipendenti e un’ANOVA a una via con 2 gruppi saranno simili. ↩︎
2. Nota che se l’assunzione di normalità non è soddisfatta, molte trasformazioni possono essere applicate per migliorarla, la più comune delle quali è la trasformazione logaritmica (log() funzione in R). ↩︎
3. Nota che il test di Bartlett è anche appropriato per testare l’assunzione di varianze uguali. ↩︎
4. Un modello additivo fa l’assunzione che le 2 variabili esplicative siano indipendenti; non interagiscono tra di loro. ↩︎
5. Dove mod è il nome del tuo modello salvato. ↩︎
6. Qui, utilizziamo la correzione di Benjamini & Hochberg (1995), ma puoi scegliere tra diversi metodi. Vedi ?p.adjust per maggiori dettagli. ↩︎

Articoli correlati

• ANOVA in R
• Test t di Student in R e a mano: come confrontare due gruppi in diversi scenari?
• Test di Wilcoxon per campioni singoli in R
• Test di Kruskal-Wallis, o la versione non parametrica della ANOVA
• Test di ipotesi a mano

Originariamente pubblicato su https://statsandr.com il 19 giugno 2023.