Un’analisi approfondita della scienza dell’Aspettativa Statistica.

'A thorough analysis of the science of Statistical Expectation.'

Come ci aspettiamo qualcosa, cosa significa aspettarsi qualsiasi cosa e la matematica che determina il significato.

Era l’estate del 1988 quando sono salito su una barca per la prima volta nella mia vita. Era un traghetto passeggeri da Dover, in Inghilterra, a Calais, in Francia. Non lo sapevo allora, ma stavo cogliendo gli ultimi sprazzi dell’era d’oro delle traversate del Canale in traghetto. Questo è stato subito prima che le compagnie aeree low-cost e il Tunnel della Manica mettessero quasi fine a ciò che penso sia il modo migliore per effettuare quel viaggio.

Mi aspettavo che il traghetto assomigliasse a una delle tante barche che avevo visto nei libri per bambini. Invece, ciò su cui mi sono imbattuto era un grattacielo bianco splendente e impossibilmente grande, con piccoli finestroni quadrati. E il grattacielo sembrava essere appoggiato di lato per qualche motivo confuso. Dalla mia angolazione di visione sul molo, non potevo vedere lo scafo e i camini della nave. Tutto ciò che vedevo era la sua lunga, piatta, finestrata esternità. Stavo guardando un grattacielo orizzontale.

Ripensando a quei momenti, è divertente reinterpretare la mia esperienza nel linguaggio delle statistiche. Il mio cervello aveva calcolato la forma prevista di un traghetto dal campione di dati di immagini di barche che avevo visto. Ma il mio campione era alquanto non rappresentativo della popolazione e ciò rendeva la media campionaria altrettanto non rappresentativa della media della popolazione. Stavo cercando di decodificare la realtà usando una media campionaria fortemente sbilanciata.

Mal di mare

Inoltre, questo viaggio attraverso il Canale fu anche la prima volta che mi sono ammalato di mare. Si dice che quando si soffre di mal di mare si debba uscire sul ponte, respirare l’aria fresca e fresca del mare e fissare l’orizzonte. L’unica cosa che funziona veramente per me è sedermi, chiudere gli occhi e sorseggiare la mia bibita preferita fino a quando i miei pensieri si allontanano lentamente dalla nausea che mi assale. A proposito, non mi sto allontanando lentamente dall’argomento di questo articolo. Arriverò subito alle statistiche. Nel frattempo, permettetemi di spiegare la mia comprensione del perché si diventa malati su una nave, in modo che possiate vedere la connessione con l’argomento in questione.

• Costo dello sviluppo di AI conversazionale nel sistema bancario nel 2023.
• David Autor nominato Scienziato Distinguito NOMIS 2023
• Artista Tecnico costruisce un grande Mammut lanoso con NVIDIA Omniverse USD Composer in questa settimana Nello Studio NVIDIA.

Nella maggior parte dei giorni della tua vita, non sei scosso su una nave. Sulla terraferma, quando inclini il tuo corpo da un lato, i tuoi orecchi interni e ogni muscolo del tuo corpo dicono al tuo cervello che ti stai inclinando da un lato. Sì, anche i tuoi muscoli parlano al tuo cervello! I tuoi occhi confermano con entusiasmo tutto questo feedback e tu esci fuori dall’esperienza senza problemi. Ma su una nave, tutto si scombina in questo affabile patto tra occhio e orecchio.

Su una nave, quando il mare fa inclinare, oscillare, dondolare, rotolare, deriva, ondeggia o qualsiasi altra cosa, ciò che i tuoi occhi dicono al tuo cervello può essere notevolmente diverso da ciò che i tuoi muscoli e il tuo orecchio interno dicono al tuo cervello. Il tuo orecchio interno potrebbe dire: “Fai attenzione! Ti stai inclinando a sinistra. Dovresti regolare la tua aspettativa di come apparirà il tuo mondo”. Ma i tuoi occhi stanno dicendo: “Nonsense! Il tavolo su cui sto seduto sembra perfettamente livellato per me, così come il piatto di cibo che vi sta sopra. L’immagine sul muro della cosa che sta urlando sembra anche dritta e livellata. Non ascoltare l’orecchio”.

I tuoi occhi potrebbero riferirti qualcosa di ancora più confuso al tuo cervello, come “Sì, ti stai inclinando. Ma la pendenza non è significativa o rapida come i tuoi orecchi interni troppo zelanti potrebbero farti credere”.

È come se i tuoi occhi e i tuoi orecchi interni stessero chiedendo al tuo cervello di creare due aspettative diverse su come il tuo mondo sta per cambiare. Il tuo cervello ovviamente non può farlo. Si confonde. E per ragioni sepolte nell’evoluzione, il tuo stomaco esprime un forte desiderio di vuotare il suo contenuto.

Cerchiamo di spiegare questa situazione terribile utilizzando il quadro del ragionamento statistico. Questa volta, useremo un po’ di matematica per aiutare la nostra spiegazione.

Dovresti aspettarti di avere il mal di mare? Entriamo nelle statistiche del mal di mare

Definiamo una variabile casuale X che assume due valori: 0 e 1. X è 0 se i segnali dai tuoi occhi non sono d’accordo con i segnali dai tuoi orecchi interni. X è 1 se lo sono:

In teoria, ogni valore di X dovrebbe avere una certa probabilità P( X =x). Le probabilità P( X =0) e P( X =1) costituiscono insieme la Funzione di Massa di Probabilità di X. La esprimiamo come segue:

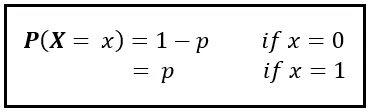
Per la maggior parte delle volte, i segnali dai tuoi occhi saranno d’accordo con i segnali dai tuoi orecchi interni. Quindi p è quasi pari a 1 e (1 — p) è un numero veramente piccolo.

Proponiamo una wild guess riguardo al valore di (1 — p). Utilizzeremo la seguente linea di ragionamento per arrivare a una stima: secondo le Nazioni Unite, l’aspettativa di vita media degli esseri umani alla nascita nel 2023 è di circa 73 anni. In secondi, ciò corrisponde a 2302128000 (circa 2,3 miliardi). Supponiamo che un individuo medio provi il mal di mare per 16 ore della sua vita, che equivale a 28800 secondi. Ora non discutiamo dei 16 ore. Ricorda che è solo una stima. Quindi, 28800 secondi ci danno una stima lavorativa di (1 — p) di 28000/2302128000 = 0,0000121626 e p=(1—0,0000121626) = 0,9999878374. Quindi, durante qualsiasi secondo della vita media di una persona, la probabilità incondizionata di sperimentare il mal di mare è solo dello 0,0000121626.

Con queste probabilità, eseguiremo una simulazione della durata di 1 miliardo di secondi nella vita di un certo John Doe. Questo è circa il 50% della vita simulata di JD. JD preferisce passare la maggior parte del tempo su terreno solido. Prende occasionalmente una crociera sul mare in cui spesso si ammala. Simuleremo se J sperimenterà il mal di mare durante ciascuno dei 1 miliardo di secondi della simulazione. Per farlo, condurremo 1 miliardo di prove di una variabile casuale di Bernoulli avente probabilità di p e (1 — p). L’esito di ogni prova sarà 1 se J si ammala, o 0 se J non si ammala. Dopo aver condotto questo esperimento, otterremo 1 miliardo di risultati. Anche tu puoi eseguire questa simulazione utilizzando il seguente codice Python:

import numpy as npp = 0.9999878374num_trials = 1000000000outcomes = np.random.choice([0, 1], size=num_trials, p=[1 - p, p])

Contiamo il numero di risultati di valore 1 (=non malato) e 0 (=ammalato):

num_outcomes_in_which_not_seasick = sum(outcomes)num_outcomes_in_which_seasick = num_trials - num_outcomes_in_which_not_seasick

Stampiamo questi conteggi. Quando li ho stampati io, ho ottenuto i seguenti valori. Potresti ottenere risultati leggermente diversi ogni volta che esegui la simulazione:

num_outcomes_in_which_not_seasick= 999987794num_outcomes_in_which_seasick= 12206

Ora possiamo calcolare se JD dovrebbe aspettarsi di avere il mal di mare in uno di quei 1 miliardo di secondi.

L’aspettativa è calcolata come la media ponderata delle due possibili uscite: uno e zero, i pesi sono le frequenze delle due uscite. Quindi eseguiamo questo calcolo:

L’output atteso è 0,999987794 che è praticamente 1,0. La matematica ci sta dicendo che in qualsiasi secondo scelto a caso nei 1 miliardi di secondi della simulazione di JD, JD non dovrebbe aspettarsi di avere il mal di mare. I dati sembrano quasi proibirlo.

Ora giochiamo un po’ con la formula sopra. Inizieremo rioridinando come segue:

Quando riformulato in questo modo, vediamo emergere una deliziosa sottostruttura. I rapporti nelle due parentesi rappresentano le probabilità associate alle due uscite, specificamente le probabilità campionarie derivate dal nostro campione di dati di 1 miliardo, piuttosto che le probabilità di popolazione. Sono probabilità campionarie perché le abbiamo calcolate utilizzando i dati dal nostro campione di dati di 1 miliardo. Detto questo, i valori 0,999987794 e 0,000012206 dovrebbero essere abbastanza vicini ai valori di popolazione di p e (1 – p) rispettivamente.

Inserendo le probabilità, possiamo riformulare la formula per l’attesa come segue:

Si noti che abbiamo usato la notazione per l’aspettativa, che è E(). Poiché X è una variabile casuale Bernoulli(p), la formula sopra ci mostra anche come calcolare il valore atteso di una variabile casuale Bernoulli. Il valore atteso di X ~ Bernoulli(p) è semplicemente p.

Delle medie campionarie, delle medie di popolazione e di una parola per farti sembrare cool

E( X ) è anche chiamata la media di popolazione, indicata da μ, perché utilizza le probabilità p e (1 – p) che sono i valori di probabilità a livello di popolazione. Queste sono le probabilità “vere” che osserverai se avessi accesso a tutta la popolazione di valori, cosa che praticamente non accade mai. Gli statistici usano la parola “asintotico” quando si riferiscono a queste e simili misure. Sono chiamati asintotici perché il loro significato è significativo solo quando qualcosa, come la dimensione del campione, si avvicina all’infinito o alla dimensione di tutta la popolazione. Ecco la cosa: penso che alle persone piaccia semplicemente dire ‘asintotico’. E penso anche che sia una copertura comoda per la scomoda verità che non puoi mai misurare il valore esatto di nulla.

Ad ogni modo, l’impossibilità di mettere le mani sulla popolazione è “il grande livellatore” nel campo della scienza statistica. Che tu sia appena uscito dall’università o un premio Nobel in Economia, quella porta alla “popolazione” rimane saldamente chiusa per te. Come statistico, sei relegato a lavorare con il campione le cui mancanze devi sopportare in silenzio. Ma non è davvero uno stato così male come sembra. Immagina cosa succederebbe se iniziassi a conoscere i valori esatti delle cose. Se avessi accesso alla popolazione. Se potessi calcolare la media, la mediana e la varianza con precisione millimetrica. Se potessi predire il futuro con precisione al centesimo. Ci sarebbe poco bisogno di stimare qualsiasi cosa. Le grandi branche della statistica cesserebbero di esistere. Il mondo avrebbe bisogno di centinaia di migliaia di statistici in meno, per non parlare dei data scientist. Immagina l’impatto sulla disoccupazione, sull’economia mondiale, sulla pace mondiale…

Ma torniamo al discorso principale. Se X è di tipo Bernoulli(p), per calcolare E( X ) non puoi utilizzare i valori reali della popolazione di p e (1 — p). Invece, devi accontentarti di stime di p e (1 — p). Queste stime le calcolerai non utilizzando l’intera popolazione — non c’è possibilità di farlo. Invece, più spesso che no, le calcolerai utilizzando un campione di dati di dimensioni modeste. E così con grande rammarico devo informarti che il meglio che puoi fare è ottenere una stima del valore atteso della variabile casuale X. Seguendo la convenzione, indichiamo la stima di p come p_hat (p con un piccolo cappello o cappello sopra) e indichiamo il valore atteso stimato come E_cap( X ).

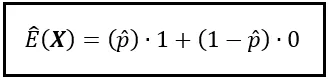
Dato che E_cap( X ) utilizza probabilità campionarie , viene chiamata media campionaria. Viene indicata con x̄ o ‘x bar’. È una x con una barra posta sulla sua testa.

La media della popolazione e la media campionaria sono il Batman e il Robin delle statistiche.

Una grande quantità di Statistica è dedicata al calcolo della media campionaria e all’utilizzo della media campionaria come stima della media della popolazione.

Ecco fatto — la vasta estensione delle Statistiche riassunta in una singola frase. 😉

Tuffandosi nell’estremità profonda dell’aspettativa

Il nostro esempio mentale con la variabile casuale di Bernoulli è stato istruttivo in quanto ha svelato in qualche modo la natura dell’aspettativa. La variabile di Bernoulli è una variabile binaria, ed è stato semplice lavorarci. Tuttavia, le variabili casuali con cui lavoriamo spesso possono assumere molti valori diversi. Fortunatamente, possiamo facilmente estendere il concetto e la formula dell’aspettativa a variabili casuali a molti valori. Illustreremo con un altro esempio.

Il valore atteso di una variabile casuale discreta a molti valori

La seguente tabella mostra un sottoinsieme di un dataset di informazioni su 205 automobili. In particolare, la tabella mostra il numero di cilindri all’interno del motore di ogni veicolo.

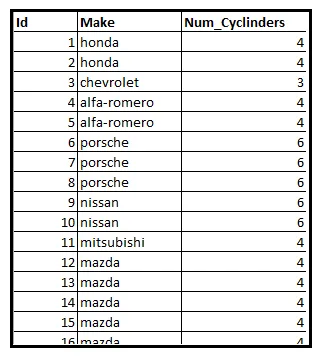
Sia Y una variabile casuale che contiene il numero di cilindri di un veicolo scelto a caso da questo dataset. Sappiamo che il dataset contiene veicoli con conteggi di cilindri di 2, 3, 4, 5, 6, 8 o 12. Quindi l’intervallo di Y è l’insieme E=[2, 3, 4, 5, 6, 8, 12].

Aggregheremo le righe di dati per conteggio di cilindri. La tabella qui sotto mostra i conteggi raggruppati. L’ultima colonna indica la corrispondente probabilità campionaria di occorrenza di ogni conteggio. Questa probabilità viene calcolata dividendo la dimensione del gruppo per 205:

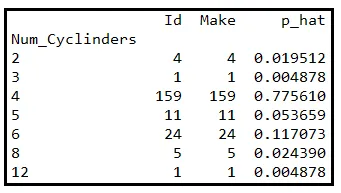
Utilizzando le probabilità campionarie, possiamo costruire la Funzione di Massa di Probabilità P( Y ) per Y. Se la plottiamo contro Y, appare così:

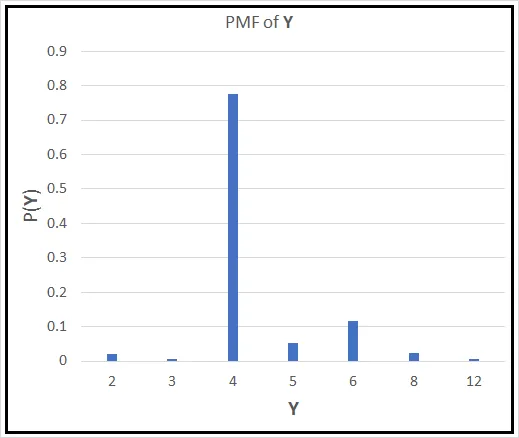
Se un veicolo scelto casualmente si presenta davanti a te, quale sarà il valore atteso dei suoi cilindri? Solo guardando la PMF, il numero che dovrai indovinare è 4. Tuttavia, c’è una matematica fredda e dura che supporta questa supposizione. Similmente a X di Bernoulli, puoi calcolare il valore atteso di Y come segue:

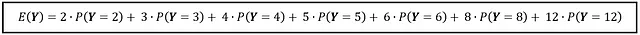
Se si calcola la somma, si ottiene 4,38049 che è abbastanza vicino alla tua supposizione di 4 cilindri.

Dato che l’intervallo di Y è l’insieme E= [2,3,4,5,6,8,12], si può esprimere questa somma come una sommatoria su E come segue:

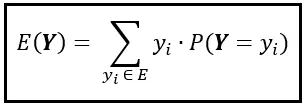
Si può utilizzare la formula sopra per calcolare il valore atteso di qualsiasi variabile casuale discreta il cui intervallo è l’insieme E.

Il valore atteso di una variabile casuale continua

Se si sta lavorando con una variabile casuale continua, la situazione cambia un po’, come descritto di seguito.

Torniamo al nostro dataset di veicoli. In particolare, guardiamo le lunghezze dei veicoli:

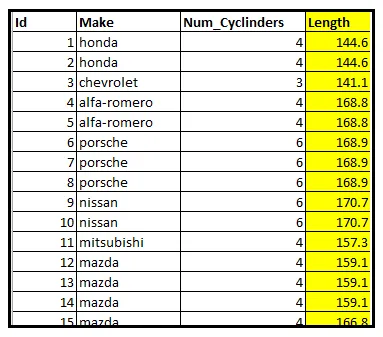
Supponiamo che Z rappresenti la lunghezza in pollici di un veicolo selezionato casualmente. L’intervallo di Z non è più un insieme discreto di valori. Invece, è un sottoinsieme dell’insieme ℝ dei numeri reali. Poiché le lunghezze sono sempre positive, è l’insieme di tutti i numeri reali positivi, indicato come ℝ >0.

Poiché l’insieme di tutti i numeri reali positivi ha un numero (incontabilmente) infinito di valori, non ha senso assegnare una probabilità a un valore individuale di Z. Se non mi credi, considera un rapido esperimento mentale: immagina di assegnare una probabilità positiva a ogni possibile valore di Z. Troverai che le probabilità sommeranno all’infinito, il che è assurdo. Quindi, la probabilità P( Z =z) semplicemente non esiste. Invece, devi lavorare con la funzione densità di probabilità f( Z =z) che assegna una densità di probabilità a diversi valori di Z.

In precedenza abbiamo discusso come calcolare il valore atteso di una variabile casuale discreta utilizzando la funzione di massa di probabilità.

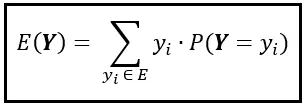
Possiamo riutilizzare questa formula per le variabili casuali continue? La risposta è sì. Per sapere come, immaginati con un microscopio elettronico.

Prendi quel microscopio e focalizzalo sull’intervallo di Z che è l’insieme di tutti i numeri reali positivi (ℝ >0). Ora, ingrandisci su un intervallo impossibilmente piccolo (z, z+δz], all’interno di questo intervallo. A questa scala microscopica, potresti osservare che, per tutti gli scopi pratici (ora, non è un termine utile), la densità di probabilità f(Z =z) è costante su δz. Di conseguenza, il prodotto di f(Z =z) e δz può approssimare la probabilità che la lunghezza di un veicolo selezionato casualmente cada nell’intervallo aperto-chiuso (z, z+δz].

Armato di questa probabilità approssimativa, puoi approssimare il valore atteso di Z come segue:

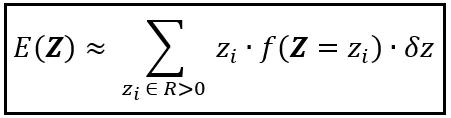
Nota come siamo passati dalla formula per E(Y) a questa approssimazione. Per arrivare a E(Z) da E(Y), abbiamo fatto quanto segue:

• Abbiamo sostituito i valori discreti y_i con i valori reali z_i.
• Abbiamo sostituito P(Y =y), che è la PMF di Y, con f(Z =z)δz, che è la probabilità approssimativa di trovare z nell’intervallo microscopico (z, z+δz].
• Invece di sommare sull’intervallo discreto e finito di Y, che è E, abbiamo sommato sull’intervallo continuo e infinito di Z, che è ℝ >0.
• Infine, abbiamo sostituito il segno di uguale con il segno di approssimazione. E qui sta la nostra colpa. Abbiamo barato. Abbiamo inserito la probabilità f(Z =z)δz come approssimazione della probabilità esatta P(Z =z). Abbiamo barato perché la probabilità esatta, P(Z =z), non può esistere per una Z continua. Dobbiamo porre rimedio a questa trasgressione, ed è esattamente ciò che faremo dopo.

Ora eseguiremo il nostro colpo di maestro, la nostra pièce de résistance, e nel farlo, ci redimeremo.

Dato che ℝ >0 è l’insieme dei numeri reali positivi, ci sono un numero infinito di intervalli microscopici di dimensione δz in ℝ >0. Pertanto, la somma su ℝ >0 è una somma su un numero infinito di termini. Questo fatto ci presenta la perfetta opportunità di sostituire la sommatoria approssimativa con un integrale esatto, come segue:

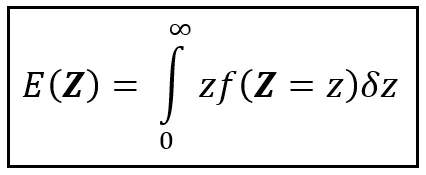
In generale, se l’intervallo di Z è l’intervallo di valori reali [a, b], impostiamo i limiti dell’integrale definito su a e b anziché su 0 e ∞.

Se conosci la PDF di Z e se l’integrale di z volte f(Z =z) esiste su [a, b], risolverai l’integrale sopra e otterrai E(Z) per i tuoi sforzi.

Se Z è distribuito uniformemente sull’intervallo [a, b], la sua PDF è la seguente:

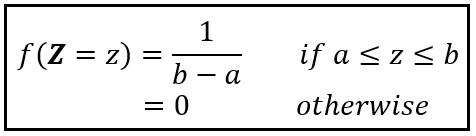
Se imposti a=1 e b=5,

f( Z =z) = 1/(5–1) = 0,25.

La densità di probabilità è una costante 0,25 da Z =1 a Z =5 ed è zero ovunque altro. Ecco come appare la PDF di Z:

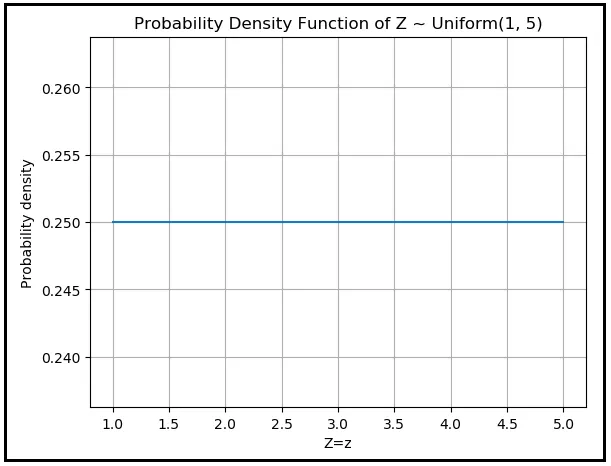
È essenzialmente una linea orizzontale piatta e continua da (1,0,25) a (5,0,25) ed è zero ovunque altro.

In generale, se la densità di probabilità di Z è uniformemente distribuita sull’intervallo [a, b], la PDF di Z è 1/(b-a) sull’intervallo [a, b] e zero altrove. Puoi calcolare E (Z) utilizzando la seguente procedura:

Se a=1 e b=5, la media di Z ~ Uniform(1, 5) è semplicemente (1+5)/2 = 3. Ciò concorda con la nostra intuizione. Se ogni uno dei valori infiniti compresi tra 1 e 5 è altrettanto probabile, ci aspetteremmo che la media si riduca alla semplice media di 1 e 5.

Ora odio sgonfiare il tuo spirito ma, in pratica, sei più propenso a notare doppi arcobaleni che atterrano sul tuo prato anteriore rispetto a variabili casuali continue per cui userai il metodo dell’integrale per calcolare il loro valore atteso.

Vedi, le PDF dall’aspetto delizioso che possono essere integrate per ottenere il valore atteso delle variabili corrispondenti hanno l’abitudine di insediarsi negli esercizi di fine capitolo dei libri di testo universitari. Sono come i gatti domestici. Non ‘fanno all’esterno’. Ma come statistico praticante, ‘all’esterno’ è dove vivi. All’esterno, ti troverai a fissare campioni di dati di valori continui come le lunghezze dei veicoli. Per modellare la PDF di tali variabili casuali del mondo reale, è probabile che utilizzerai una delle funzioni continue ben note come la Normale, la Log-Normale, la Chi-quadrato, l’Esponenziale, la Weibull e così via, o una distribuzione mista, ovvero qualsiasi cosa sembri adattarsi meglio ai tuoi dati.

Ecco un paio di tali distribuzioni:

Per molte PDF comunemente usate, qualcuno ha già preso la briga di derivare la media della distribuzione mediante l’integrazione (x volte f(x)) proprio come abbiamo fatto con la distribuzione Uniforme. Ecco un paio di tali distribuzioni:

Infine, in alcune situazioni, effettivamente in molte situazioni, i dataset della vita reale presentano schemi troppo complessi per essere modellati da una qualsiasi di queste distribuzioni. È come quando ti imbatti in un virus che ti assale con una serie di sintomi. Per aiutarti a superarli, il tuo medico ti prescrive un mix di farmaci, ognuno con una diversa potenza, dosaggio e meccanismo d’azione. Quando sei assalito da dati che presentano molti schemi complessi, devi impiegare un piccolo esercito di distribuzioni di probabilità per modellarli. Una tale combinazione di diverse distribuzioni è nota come una distribuzione mista. Una miscela comunemente usata è la potente Miscela Gaussiana, che è una somma pesata di diverse funzioni di densità di probabilità di diverse variabili casuali normalmente distribuite, ognuna con una diversa combinazione di media e varianza.

Dato un campione di dati reali, potresti trovarti a fare qualcosa terribilmente semplice: prenderai la media della colonna di dati a valore continuo e la ungerai come media del campione. Ad esempio, se calcoli la lunghezza media delle automobili nel dataset delle automobili, arrivi a 174.04927 pollici, e basta così. Tutto fatto. Ma non è così, e non è tutto fatto. Perché c’è ancora una domanda a cui devi rispondere.

Quanto è buona la tua media campionaria? Avere un’idea della sua precisione

Come sai quanto accurata è la stima della media della popolazione della tua media campionaria? Mentre raccoglievi i dati, potresti essere stato sfortunato, o pigro, o “vincolato ai dati” (che spesso è un’eccellente eufemismo per la buona vecchia pigrizia). In ogni caso, stai fissando un campione che non è proporzionalmente casuale. Non rappresenta proporzionalmente le diverse caratteristiche della popolazione. Prendiamo ad esempio il dataset delle automobili: potresti aver raccolto dati per un gran numero di automobili di dimensioni Nisoo e troppo poche automobili grandi. E le limousine potrebbero essere completamente assenti dal tuo campione. Di conseguenza, la lunghezza media che calcoli sarà eccessivamente sbilanciata verso la lunghezza media solo delle automobili di dimensioni Nisoo nella popolazione. Che ti piaccia o meno, stai ora lavorando sulla base del fatto che praticamente tutti guidano un’automobile di dimensioni Nisoo.

Sii veritiero con te stesso

Se hai raccolto un campione fortemente sbilanciato e non lo sai o non ti interessa, allora il cielo ti aiuti nella tua carriera scelta. Ma se sei disposto a prendere in considerazione la possibilità di un bias e hai qualche indizio su quale tipo di dati potresti essere mancante (ad esempio auto sportive), allora le statistiche ti verranno in soccorso con potenti meccanismi per aiutarti a stimare questo bias.

Purtroppo, non importa quanto ci provi, non sarai mai in grado di raccogliere un campione perfettamente bilanciato. Contiene sempre dei bias perché le proporzioni esatte di vari elementi all’interno della popolazione rimangono per sempre inaccessibili. Ricorda quella porta verso la popolazione? Ricorda come il cartello sopra di essa dica sempre “CHIUSO”?

Il tuo corso di azione più efficace è raccogliere un campione che contenga circa le stesse frazioni di tutte le cose che esistono nella popolazione, il cosiddetto campione ben bilanciato. La media di questo campione ben bilanciato è la migliore media campionaria possibile con cui puoi partire.

Ma le leggi della natura non sempre tolgono il vento dalle barche a vela degli statistici. Esiste una magnifica proprietà della natura espressa in un teorema chiamato Teorema del Limite Centrale (CLT). Puoi usare il CLT per determinare quanto bene la tua media campionaria stima la media della popolazione.

Il CLT non è una soluzione miracolosa per affrontare campioni fortemente sbilanciati. Se il tuo campione consiste prevalentemente di automobili di media grandezza, hai effettivamente ridefinito la tua idea di popolazione. Se stai studiando intenzionalmente solo automobili di media grandezza, sei assolto. In questa situazione, sentiti libero di usare il CLT. Ti aiuterà a stimare quanto la tua media campionaria si avvicina alla media della popolazione delle automobili di media grandezza.

D’altra parte, se il tuo scopo esistenziale è studiare l’intera popolazione di veicoli mai prodotti, ma il tuo campione contiene principalmente automobili di media grandezza, hai un problema. Per lo studente di statistica, lasciatemi riformulare quella frase con parole leggermente diverse. Se la tua tesi di laurea è su quante volte gli animali domestici sbadigliano, ma i tuoi partecipanti sono 20 gatti e il Barboncino del tuo vicino, allora, con o senza CLT, nessuna quantità di abilità statistica ti aiuterà a valutare l’accuratezza della tua media campionaria.

L’essenza del teorema del limite centrale

Una comprensione completa del teorema del limite centrale richiede un altro articolo, ma l’essenza di ciò che afferma è la seguente:

Se si estrae un campione casuale di punti dati dalla popolazione e si calcola la media del campione, e si ripete questo esercizio molte volte, si otterranno… molte diverse medie campionarie. Beh, ovvio! Ma succede qualcosa di sorprendente. Se si traccia una distribuzione di frequenza di tutte queste medie campionarie, si vedrà che sono sempre distribuite normalmente. Inoltre, la media di questa distribuzione normale è sempre la media della popolazione che si sta studiando. È questa inquietante e affascinante caratteristica della personalità del nostro universo che il teorema del limite centrale descrive utilizzando (cosa altro?) il linguaggio della matematica.

Vediamo come usare il teorema del limite centrale. Inizieremo così:

Utilizzando la media campionaria Z _bar da un solo campione, affermiamo che la probabilità che la media della popolazione μ si trovi nell’intervallo [μ_low, μ_high] è (1 — α):

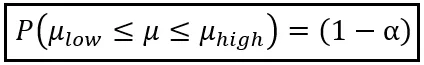
È possibile impostare α su qualsiasi valore compreso tra 0 e 1. Ad esempio, se si imposta α su 0,05, si otterrà (1 — α) come 0,95, cioè 95%.

E affinché questa probabilità (1 — α) sia vera, i limiti μ_low e μ_high devono essere calcolati come segue:

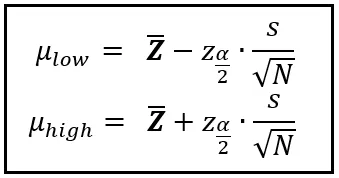
Nelle equazioni sopra, sappiamo cosa sono Z _bar, α, μ_low e μ_high. Il resto dei simboli merita qualche spiegazione.

La variabile s è la deviazione standard del campione di dati.

N è la dimensione del campione.

Arriviamo infine a z_α/2.

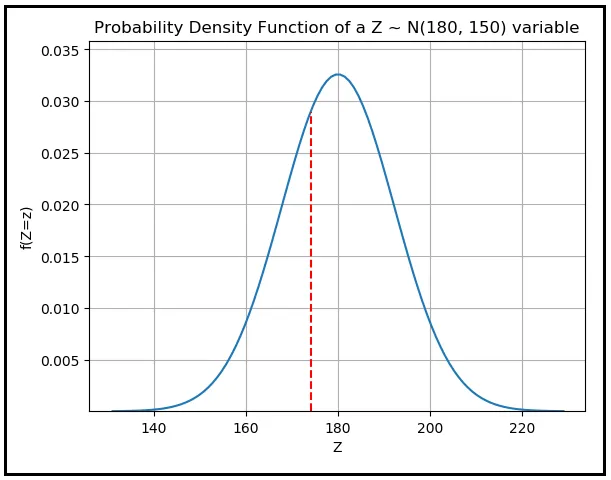
z_α/2 è un valore che si legge sull’asse X della PDF della distribuzione normale standard. La distribuzione normale standard è la PDF di una variabile casuale continua normalmente distribuita che ha una media zero e una deviazione standard di uno. z_α/2 è il valore sull’asse X di tale distribuzione per il quale l’area sotto la PDF che giace alla sinistra di quel valore è (1 — α/2). Ecco come appare questa area quando si imposta α su 0,05:

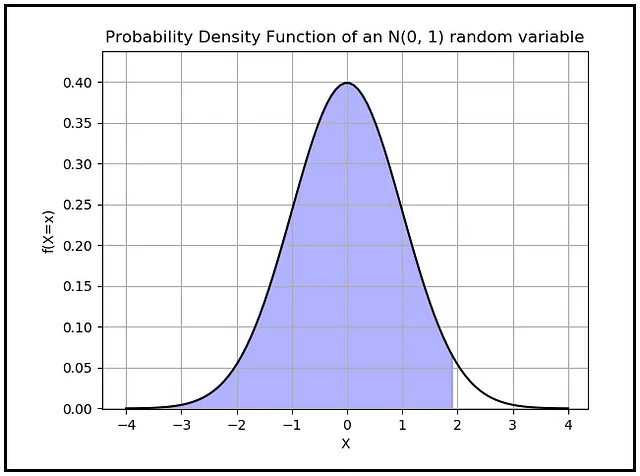
L’area di colore blu è calcolata come (1 — 0,05/2) = 0,975. Ricorda che l’area totale sotto qualsiasi curva PDF è sempre 1,0.

Per riassumere, una volta calcolata la media (Z _bar) da un solo campione, è possibile costruire limiti intorno a questa media in modo che la probabilità che la media della popolazione si trovi entro quei limiti sia un valore a scelta.

Riesaminiamo le formule per stimare questi limiti:

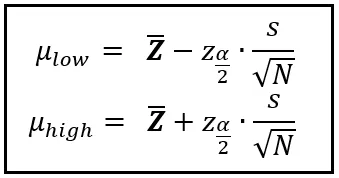
Queste formule ci danno un paio di intuizioni sulla natura della media campionaria:

1. All’aumentare della varianza s del campione, il valore del limite inferiore (μ_basso) diminuisce, mentre quello del limite superiore (μ_alto) aumenta. Ciò sposta efficacemente μ_basso e μ_alto l’uno dall’altro e lontano dalla media del campione. Al contrario, all’aumentare della varianza del campione, μ_basso si avvicina a Z _bar dall’alto, e μ_alto si avvicina a Z _bar dal basso. I limiti dell’intervallo convergono essenzialmente sulla media del campione da entrambi i lati. In effetti, l’intervallo [μ_basso, μ_alto] è direttamente proporzionale alla varianza del campione. Se il campione è ampiamente (o strettamente) disperso intorno alla sua media, la maggiore (o minore) dispersione riduce (o aumenta) l’affidabilità della media del campione come stima della media della popolazione.
2. Notare che la larghezza dell’intervallo è inversamente proporzionale alla dimensione del campione (N). Tra due campioni che mostrano una varianza simile, il campione più grande darà un intervallo più stretto intorno alla sua media rispetto al campione più piccolo.

Vediamo come calcolare questo intervallo per il dataset di automobili. Calcoleremo [μ_basso, μ_alto] in modo che ci sia una possibilità del 95% che la media della popolazione μ si trovi in questi limiti.

Per avere una possibilità del 95%, dovremmo impostare α su 0,05 in modo che (1 — α) = 0,95.

Sappiamo che Z _bar è 174,04927 pollici.

N sono 205 veicoli.

La deviazione standard del campione può essere facilmente calcolata. È di 12,33729 pollici.

Successivamente, lavoreremo su z_α/2. Poiché α è 0,05, α/2 è 0,025. Vogliamo trovare il valore di z_α/2, ovvero z_0,025. Questo è il valore sull’asse X della curva PDF della variabile casuale normale standard, dove l’area sotto la curva è (1 — α/2) = (1 — 0,025) = 0,975. Rifacendoci alla tabella per la distribuzione normale standard, troviamo che questo valore corrisponde all’area a sinistra di X =1,96.

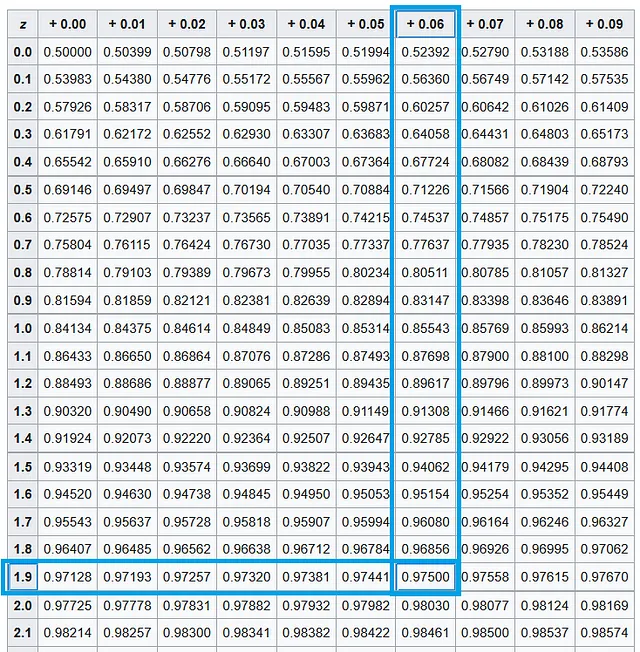
Inserendo tutti questi valori, otteniamo i seguenti limiti:

μ_basso = Z_bar — ( z_α/2 · s/√N) = 174,04927 — (1,96 · 12,33729/205) = 173,93131

μ_alto = Z_bar + ( z_α/2 · s/√N) = 174,04927 + (1,96 · 12,33729/205) = 174,16723

Quindi, [μ_basso, μ_alto] = [173,93131 pollici, 174,16723 pollici]

C’è una possibilità del 95% che la media della popolazione si trovi in questo intervallo. Guarda quanto è stretto questo intervallo. La sua larghezza è solo 0,23592 pollici. All’interno di questa piccola fessura si trova la media del campione di 174,04927 pollici. Nonostante tutti i bias che possono essere presenti nel campione, la nostra analisi suggerisce che la media del campione di 174,04927 pollici sia una stima notevolmente buona della media della popolazione sconosciuta.

Andare oltre la prima dimensione: Aspettativa in uno spazio di campionamento multi-dimensionale

Fino ad ora, la nostra discussione sull’aspettativa è stata limitata a una singola dimensione, ma non è necessario. Possiamo facilmente estendere il concetto di aspettativa a due, tre o più dimensioni. Per calcolare l’aspettativa su uno spazio multidimensionale, tutto ciò di cui abbiamo bisogno è una funzione di densità di probabilità congiunta definita sullo spazio N-dimensionale. Una funzione di densità di probabilità congiunta prende più variabili casuali come parametri e restituisce la probabilità di osservare congiuntamente quei valori.

In precedenza nell’articolo, abbiamo definito una variabile casuale Y che rappresenta il numero di cilindri in un veicolo scelto casualmente dal dataset degli auto. Y è la tua tipica variabile casuale discreta monodimensionale e il suo valore atteso è dato dalla seguente equazione:

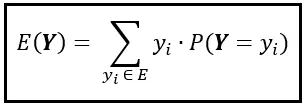
Introduciamo una nuova variabile casuale discreta, X. La funzione di massa di probabilità congiunta di X e Y è indicata da P( X =x_i, Y =y_j), o semplicemente come P( X , Y ). Questa funzione di massa congiunta ci solleva dallo spazio accogliente e unidimensionale che Y abita e ci deposita in uno spazio bidimensionale più interessante. In questo spazio bidimensionale, un singolo punto dati o risultato è rappresentato dalla coppia (x_i, y_i). Se l’intervallo di X contiene ‘p’ risultati e l’intervallo di Y contiene ‘q’ risultati, lo spazio bidimensionale avrà (p x q) risultati congiunti. Usiamo la coppia (x_i, y_i) per indicare ciascuno di questi risultati congiunti. Per calcolare E( Y ) in questo spazio bidimensionale, dobbiamo adattare la formula di E( Y ) come segue:

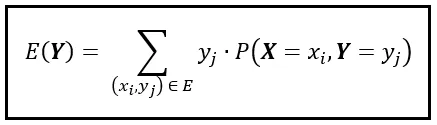
Si noti che stiamo sommando su tutte le possibili coppie (x_i, y_i) nello spazio bidimensionale. Scomponiamo questa somma in una somma annidata come segue:

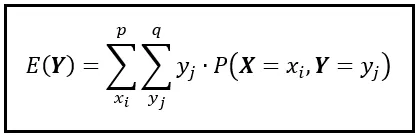
Nella somma annidata, la somma interna calcola il prodotto di y_j e P( X =x_i, Y =y_j) su tutti i valori di y_j. Quindi, la somma esterna ripete la somma interna per ogni valore di x_i. In seguito, raccoglie tutte queste somme individuali e le aggiunge per calcolare E( Y ).

Possiamo estendere la formula sopra a qualsiasi numero di dimensioni semplicemente annidando le somme l’una nell’altra. Tutto ciò di cui hai bisogno è una funzione di massa congiunta definita sullo spazio N-dimensionale. Ad esempio, ecco come estendere la formula a uno spazio a 4 dimensioni:

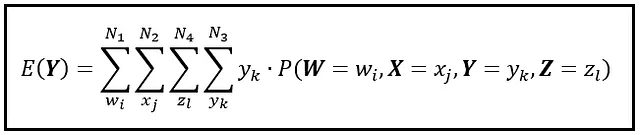
Si noti come posizioniamo sempre la somma di Y al livello più profondo. Puoi disporre le rimanenti somme in qualsiasi ordine desideri — otterrai lo stesso risultato per E( Y ).

Potresti chiederti, perché mai vorresti definire una funzione di massa di probabilità congiunta e impazzire lavorando attraverso tutte quelle sommatorie nidificate? Cosa significa E (Y) quando viene calcolato su uno spazio N-dimensionale?

Il modo migliore per capire il significato dell’aspettativa in uno spazio multidimensionale è illustrarne l’uso sui dati reali multidimensionali del mondo reale.

I dati che useremo provengono da una certa barca che, a differenza di quella che ho preso attraverso la Manica, non ha fatto tragica fine dall’altra parte.

La seguente figura mostra alcune delle righe in un set di dati di 887 passeggeri a bordo del RMS Titanic:

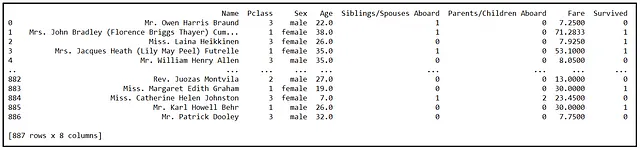
La colonna Pclass rappresenta la classe della cabina del passeggero con valori interi di 1, 2 o 3. Le variabili Siblings/Spouses Aboard e Parents/Children Aboard sono variabili binarie (0/1) che indicano se il passeggero aveva fratelli, coniugi, genitori o figli a bordo. In statistica, comunemente, e un po’ crudelmente, ci riferiamo a tali variabili indicatori binarie come variabili dummy. Non c’è nulla di testardo in esse che meriti il nomignolo denigratorio.

Come puoi vedere dalla tabella, ci sono 8 variabili che identificano congiuntamente ciascun passeggero nel set di dati. Ciascuna di queste 8 variabili è una variabile casuale. Il compito che abbiamo di fronte è triplice:

1. Vogliamo definire una funzione di massa di probabilità congiunta su un sottoinsieme di queste variabili casuali, e,
2. Usando questa funzione di massa di probabilità congiunta, vogliamo illustrare come calcolare il valore atteso di una di queste variabili su questa funzione di massa di probabilità multidimensionale, e,
3. Vogliamo capire come interpretare questo valore atteso.

Per semplificare le cose, bineremo la variabile Age in bin di dimensione 5 anni e etichetteremo i bin come 5, 10, 15, 20, …, 80. Ad esempio, un’età in bin di 20 significherà che l’età effettiva del passeggero si trova nell’intervallo di anni (15, 20]. Chiameremo la variabile casuale binata come Age_Range.

Una volta che Age è binato, raggrupperemo i dati per Pclass e Age_Range. Ecco i conteggi raggruppati:

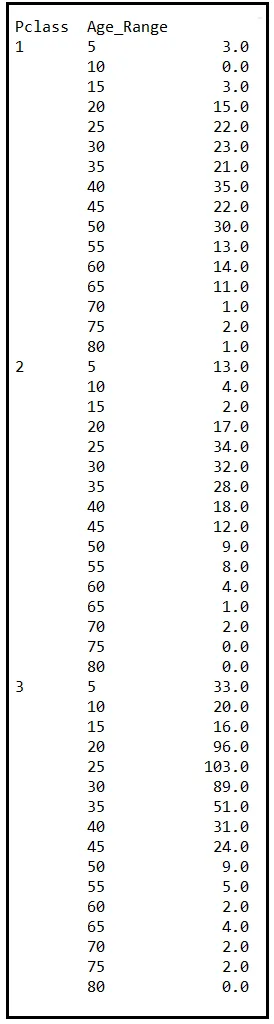
La tabella sopra contiene il numero di passeggeri a bordo del Titanic per ogni coorte (gruppo) che è definito dalle caratteristiche Pclass e Age_Range. Incidentalmente, coorte è un’altra parola (insieme ad asintotico) che gli statistici adorano. Ecco un consiglio: ogni volta che vuoi dire “gruppo”, di’ “coorte”. Ti prometto questo, qualunque cosa tu stessi pianificando di sbuffare suonerà istantaneamente dieci volte più significativa. Per illustrare: “Otto diverse coorti di appassionati di alcol (scusa, enofili) hanno bevuto del vino finto e le loro reazioni sono state registrate”. Vedi cosa intendo?

Ad essere onesti, “coorte” ha un significato preciso che “gruppo” non ha. Tuttavia, può essere istruttivo dire “coorte” ogni tanto e vedere i sentimenti di rispetto crescere sui volti dei tuoi ascoltatori.

In ogni caso, aggiungeremo un’altra colonna alla tabella delle frequenze. Questa nuova colonna conterrà la probabilità di osservare la particolare combinazione di Pclass e Age_Range. Questa probabilità, P(Pclass, Age_Range), è il rapporto tra la frequenza (cioè il numero nella colonna Name) e il numero totale di passeggeri nel dataset (cioè 887).

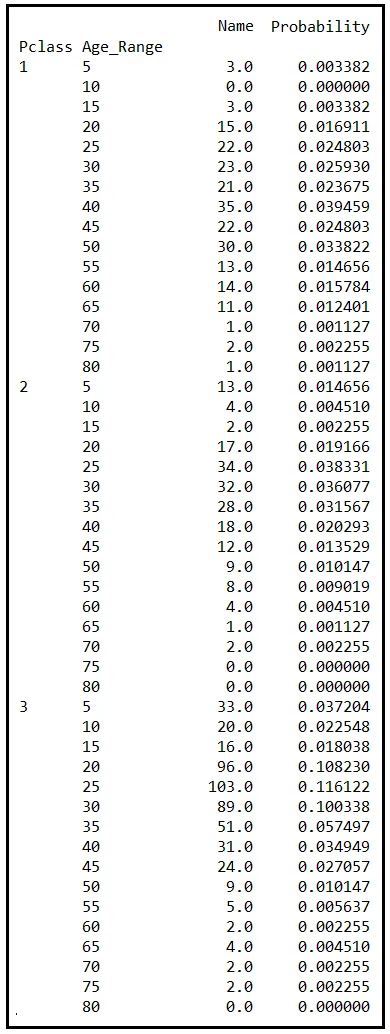
La probabilità P(Pclass, Age_Range) è la funzione di massa di probabilità congiunta delle variabili casuali Pclass e Age_Range. Ci fornisce la probabilità di osservare un passeggero descritto da una particolare combinazione di Pclass e Age_Range. Ad esempio, osservando la riga in cui Pclass è 3 e Age_Range è 25, la corrispondente probabilità congiunta è 0.116122. Tale numero ci indica che circa il 12% dei passeggeri nelle cabine di terza classe del Titanic aveva tra i 20 e i 25 anni.

Come per la PMF unidimensionale, anche la PMF congiunta si somma perfettamente a 1,0 quando valutata su tutte le combinazioni di valori delle sue variabili casuali costituenti. Se la tua PMF congiunta non si somma a 1,0, dovresti esaminare attentamente come l’hai definita. Potrebbe esserci un errore nella formula o, peggio ancora, nella progettazione del tuo esperimento.

Nel dataset sopra, la PMF congiunta si somma effettivamente a 1,0. Sentiti libero di credermi!

Per avere un’idea visiva di come la PMF congiunta, P(Pclass, Age_Range), sia fatta, puoi rappresentarla in 3 dimensioni. Nel grafico 3D, imposta l’asse X e l’asse Y rispettivamente su Pclass e Age_Range e l’asse Z sulla probabilità P(Pclass, Age_Range). Ciò che vedrai è un grafico 3D affascinante.

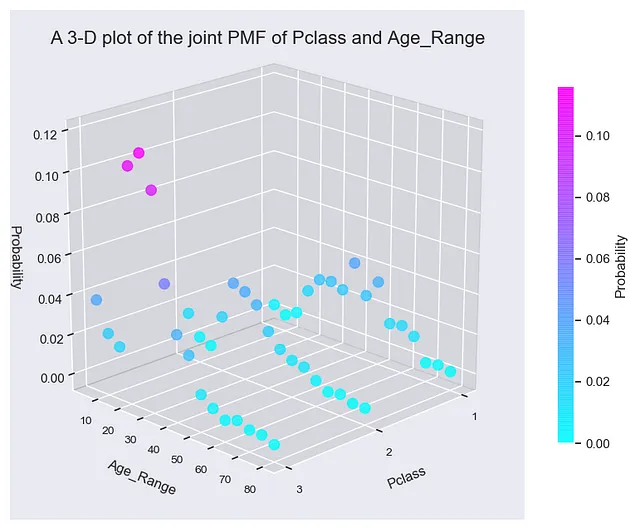
Se guardi attentamente il grafico, noterai che la PMF congiunta consiste di tre grafici paralleli, uno per ogni classe di cabina sul Titanic. Il grafico 3D mette in evidenza alcune delle caratteristiche demografiche dell’umanità a bordo della nave destinata alla sfortuna. Ad esempio, in tutte e tre le classi di cabina, sono i passeggeri tra i 15 e i 40 anni a costituire la maggior parte della popolazione.

Ora lavoriamo sul calcolo di E(Age_Range) su questo spazio 2D. E(Age_Range) è dato da:

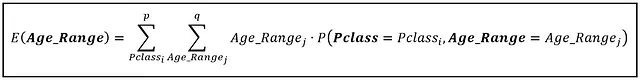
Eseguiamo la somma interna su tutti i valori di Age_Range: 5,10,15,…,80. Eseguiamo la somma esterna su tutti i valori di Pclass: [1, 2, 3]. Per ogni combinazione di (Pclass, Age_Range), scegliamo la probabilità congiunta dalla tabella. Il valore atteso di Age_Range è di 31,48252537 anni, che corrisponde al valore binario di 35. Possiamo aspettarci che il passeggero “medio” sul Titanic abbia tra i 30 e i 35 anni.

Se si prende la media della colonna Age_Range nel dataset del Titanic, si arriva esattamente allo stesso valore: 31.48252537 anni. Allora perché non prendere semplicemente la media della colonna Age_Range per ottenere E( Age_Range) ? Perché costruire una macchina di Rube Goldberg di sommatorie nidificate su uno spazio N-dimensionale solo per arrivare allo stesso valore?

È perché in alcune situazioni, tutto ciò che avrai è la PMF congiunta e gli intervalli delle variabili casuali. In questo caso, se avessi solo P( Pclass, Age_Range ) e conoscessi l’intervallo di Pclass come [1,2,3], e quello di Age_Range come [5,10,15,20,…,80], puoi comunque usare la tecnica di sommatorie nidificate per calcolare E( Pclass ) o E( Age_Range ).

Se le variabili casuali sono continue, il valore atteso su uno spazio multidimensionale può essere trovato usando un integrale multiplo. Ad esempio, se X , Y , e Z sono variabili casuali continue e f( X , Y , Z ) è la funzione di densità di probabilità congiunta definita sullo spazio continuo tridimensionale di tuple (x, y, z), il valore atteso di Y su questo spazio tridimensionale è dato nella figura seguente:

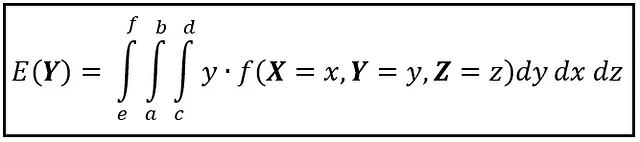
Come nel caso discreto, si integra prima sulla variabile di cui si vuole calcolare il valore atteso e poi sul resto delle variabili.

Un famoso esempio che dimostra l’applicazione del metodo dell’integrale multiplo per il calcolo dei valori attesi esiste a una scala troppo piccola per essere percepita dall’occhio umano. Mi riferisco alla funzione d’onda della meccanica quantistica. La funzione d’onda è indicata come Ψ(x, y, z, t) nelle coordinate cartesiane o come Ψ(r, θ, ɸ, t) nelle coordinate polari. Viene utilizzata per descrivere le proprietà di cose seriamente piccole che amano vivere in spazi davvero, davvero angusti, come gli elettroni in un atomo. La funzione d’onda Ψ restituisce un numero complesso della forma A + jB, dove A rappresenta la parte reale e B rappresenta la parte immaginaria. Possiamo interpretare il quadrato del valore assoluto di Ψ come una funzione di densità di probabilità congiunta definita sullo spazio quadridimensionale descritto dalla tupla (x, y, z, t) o (r, θ, ɸ, t). In particolare, per un elettrone in un atomo di idrogeno, possiamo interpretare |Ψ|² come l’approssimativa probabilità di trovare l’elettrone in un volume di spazio infinitesimale intorno a (x, y, z) o intorno a (r, θ, ɸ) al tempo t. Conoscendo |Ψ|², possiamo eseguire un integrale quadruplo su x, y, z, e t per calcolare la posizione attesa dell’elettrone lungo l’asse X, Y o Z (o i loro equivalenti polari) al tempo t.

Pensieri finali

Ho iniziato questo articolo con la mia esperienza con il mal di mare. E non ti biasimerei se avessi storpiato l’uso di una variabile casuale di Bernoulli per modellare ciò che è un’esperienza umana notevolmente complessa e in parte poco compresa. Il mio obiettivo era illustrare come l’aspettativa ci influenzi, letteralmente, a livello biologico. Un modo per spiegare quell’esperienza era utilizzare il linguaggio fresco e rassicurante delle variabili casuali.

Iniziando con la variabile di Bernoulli ingannevolmente semplice, abbiamo spazzato la nostra illustrativa spazzola su tutta la tela statistica fino alla magnifica complessità multidimensionale della funzione d’onda quantistica. In tutto ciò, abbiamo cercato di capire come l’aspettativa operi su scale discrete e continue, in dimensioni singole e multiple e a scale microscopiche.

C’è un’altra area in cui l’aspettativa ha un impatto enorme. Quell’area è la probabilità condizionata in cui si calcola la probabilità che una variabile casuale X assuma un valore “x” assumendo che alcune altre variabili casuali A, B, C, ecc. abbiano già assunto i valori “a”, “b”, “c”. La probabilità di X condizionata ad A, B e C è indicata come P( X =x| A =a, B =b, C =c) o semplicemente come P( X | A , B , C ). In tutte le formule per l’aspettativa che abbiamo visto, se sostituisci la probabilità (o la densità di probabilità) con la versione condizionale della stessa, otterrai le formule corrispondenti per l’aspettativa condizionale. Viene indicata come E( X =x| A =a, B =b, C =c) e sta alla base degli estesi campi dell’analisi di regressione e della stima. E questo è il cibo per articoli futuri!

Citazioni e diritti d’autore

Dataset

Il dataset sull’automobile è stato scaricato dal UC Irvine Machine Learning Repository sotto la licenza Creative Commons Attribution 4.0 International (CC BY 4.0).

Il dataset del Titanic è stato scaricato da Kaggle sotto la licenza CC0.

Immagini

Tutte le immagini in questo articolo sono di proprietà di Sachin Date sotto CC-BY-NC-SA, a meno che una diversa fonte e diritto d’autore non siano menzionati sotto l’immagine.

Se ti è piaciuto questo articolo, seguimi su Sachin Date per ricevere consigli, how-to e consigli di programmazione su argomenti dedicati alla regressione, all’analisi delle serie temporali e alla previsione.