Svelare il Cox un oscuro segreto nascosto della regressione di Cox.

Uncovering Cox's obscure secret hidden in Cox regression.

Perché i predittori perfetti risultano in un valore di p di 0,93?

Immergersi nei predittori perfetti

Se hai seguito i miei precedenti post sul blog, potresti ricordare che la regressione logistica incontra un problema quando cerca di adattare dati perfettamente separati, portando a un rapporto di probabilità infinito. Nella regressione di Cox, dove il rischio sostituisce le probabilità, potresti chiederti se sorge un problema simile con i predittori perfetti. Si verifica, ma a differenza della regressione logistica, è molto meno evidente come ciò accada qui e persino cosa costituisca “predittori perfetti”. Come diventerà più chiaro in seguito, i predittori perfetti sono definiti come predittori x le cui classifiche corrispondono esattamente alle classifiche dei tempi degli eventi (la loro correlazione di Spearman è uno).

Precedentemente, su “Unbox the Cox”:

Unbox the Cox: Guida intuitiva alle regressioni di Cox

Come fanno i rischi e le stime di massima verosimiglianza a prevedere le classifiche degli eventi?

towardsdatascience.com

abbiamo spiegato la massima stima di verosimiglianza e presentato un set di dati inventato con cinque soggetti, dove un singolo predittore, x, rappresentava la dose di un farmaco per prolungare la vita. Per rendere x un predittore perfetto dei tempi degli eventi, qui abbiamo scambiato i tempi degli eventi per i soggetti C e D:

• Analizza le tendenze del ghiaccio artico con Python
• Come utilizzare il metodo Pandas loc per lavorare efficientemente con il tuo DataFrame.
• Pandas 2.0 Una rivoluzione per i Data Scientist?

import numpy as npimport pandas as pdimport plotnine as p9from cox.plots import (    plot_subject_event_times,    animate_subject_event_times_and_mark_at_risk,    plot_cost_vs_beta,)perfect_df =  pd.DataFrame({    'subject': ['A', 'B', 'C', 'D', 'E'],    'time': [1, 3, 4, 5, 6],    'event': [1, 1, 1, 1, 0],    'x': [-1.7, -0.4, 0.0, 0.9, 1.2],})plot_subject_event_times(perfect_df, color_map='x')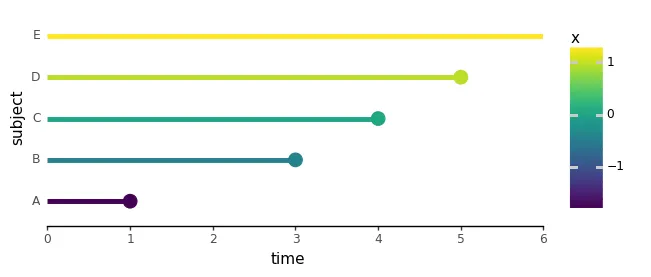

Per capire perché questi “predittori perfetti” possono essere problematici, riprendiamo da dove abbiamo lasciato e controlliamo il costo del logaritmo negativo della verosimiglianza rappresentato contro β:

negloglik_sweep_betas_perfect_df = neg_log_likelihood_all_subjects_sweep_betas(    perfect_df,    betas=np.arange(-5, 5, 0.1))plot_cost_vs_beta(negloglik_sweep_betas_perfect_df, width=0.1)

Puoi vedere subito che non c’è più un valore minimo di β: se usiamo valori molto grandi e negativi di β, otteniamo adattamenti di verosimiglianza che sono quasi perfetti per tutti gli eventi.

Ora, approfondiamo la matematica dietro questo e diamo un’occhiata alla verosimiglianza dell’evento A. Scopriremo come cambiano il numeratore e il denominatore mentre regoliamo β:

Quando β è alto o un grande numero positivo, l’ultimo termine nel denominatore (con il valore di x più grande di 1,2), rappresentando il rischio del soggetto E, domina l’intero denominatore e diventa estremamente grande. Quindi, la verosimiglianza diventa piccola e si avvicina allo zero:

Ciò comporta un grande log-negativo della probabilità. Lo stesso accade per ogni singola probabilità poiché l’ultimo rischio del soggetto E, supera sempre qualsiasi rischio nel numeratore. Di conseguenza, il log-negativo della probabilità aumenta per i soggetti A a D. In questo caso, quando abbiamo un alto β, riduce tutte le probabilità, risultando in un adattamento scarso per tutti gli eventi.

Ora, quando β è basso o un grande numero negativo, il primo termine nel denominatore, rappresentante il rischio del soggetto A, domina poiché ha il valore x più basso. Poiché lo stesso rischio del soggetto A appare anche nel numeratore, la probabilità L(A) può essere arbitrariamente vicina a 1 rendendo β sempre più negativo, creando così un adattamento quasi perfetto:

Lo stesso vale per tutte le altre probabilità individuali: i β negativi ora aumentano le probabilità di tutti gli eventi contemporaneamente. In sostanza, avere un β negativo non comporta svantaggi. Allo stesso tempo, alcuni rischi individuali aumentano (soggetti A e B con x negativo), alcuni rimangono uguali (soggetto C con x = 0) e altri diminuiscono (soggetto D con x positivo). Ma ricorda, ciò che conta veramente qui sono i rapporti tra i rischi. Possiamo verificare questa matematica a occhio plottando i rischi individuali:

def plot_likelihoods(df, ylim=[-20, 20]):    betas = np.arange(ylim[0], ylim[1], 0.5)    subjects = df.query("event == 1")['subject'].tolist()    likelihoods_per_subject = []    for subject in subjects:        likelihoods = [            np.exp(log_likelihood(df, subject, beta))            for beta in betas        ]        likelihoods_per_subject.append(            pd.DataFrame({                'beta': betas,                'likelihood': likelihoods,                'subject': [subject] * len(betas),            })                )    lik_df = pd.concat(likelihoods_per_subject)    return (        p9.ggplot(lik_df, p9.aes('beta', 'likelihood', color='subject'))        + p9.geom_line(size=2)        + p9.theme_classic()    )    plot_likelihoods(perfect_df)

Il modo in cui le probabilità vengono messe insieme, come un rapporto tra un rischio e la somma dei rischi di tutti i soggetti ancora a rischio, significa che i valori β negativi creano un adattamento perfetto per la probabilità di ogni soggetto il cui rango del tempo dell’evento è maggiore o uguale al rango del predittore! Come nota a margine, se x avesse una perfetta correlazione di Spearman negativa con i tempi degli eventi, le cose si invertirebbero: i β arbitrariamente positivi ci darebbero adattamenti arbitrariamente buoni.

Ranghi del predittore e del tempo non allineati

In realtà possiamo vedere questo e mostrarti cosa succede quando i ranghi del tempo degli eventi e dei predittori non si allineano usando un altro esempio inventato:

sample_df = pd.DataFrame({    'subject': ['A', 'B', 'C', 'D', 'E', 'F', 'G', 'H'],    'x': [-1.7, -0.4, 0.0, 0.5, 0.9, 1.2, 1.3, 1.45],    'time': [1, 2, 4, 3, 5, 7, 6, 8],    'rank_x': [1, 2, 3, 4, 5, 6, 7, 8],    'event': [1, 1, 1, 1, 1, 1, 1, 0],})sample_df

In questo particolare esempio, la colonna time varia da 1 a 8, dove ogni valore rappresenta il proprio rango. Abbiamo anche una colonna x_rank, che classifica i predittori x. Ora, ecco l’osservazione chiave: per i soggetti D e G, il loro x_rank è effettivamente superiore al loro corrispondente rango del time. Di conseguenza, le probabilità di D e G non subiranno l’effetto di cancellazione tra numeratore e denominatore quando abbiamo grandi valori negativi di β:

Ora le loro probabilità sono massimali ad alcuni valori intermedi finiti di β . Diamo un’occhiata a un grafico delle probabilità individuali per vedere questo:

plot_likelihoods(sample_df)

Questi ranghi “sfasati” tra un tempo e un predittore giocano un ruolo cruciale: impediscono a tutte le probabilità di collassare essenzialmente in una sola quando abbiamo β s significativamente negativi.

In conclusione, in regressione di Cox, per ottenere un coefficiente β finito per un predittore x , è necessario almeno un’istanza in cui il rango del predittore x è inferiore al rango del tempo dell’evento.

La perfezione è davvero nemica del bene (p-value)

Quindi, come si comportano questi predittori perfetti in scenari reali? Beh, per scoprirlo, rivolgiamoci ancora una volta alla libreria lifelines per una qualche indagine:

from lifelines import CoxPHFitterperfect_cox_model = CoxPHFitter()perfect_cox_model.fit(  perfect_df,  duration_col='time',  event_col='event',  formula='x')perfect_cox_model.print_summary()

#> /.../coxph_fitter.py:1586: ConvergenceWarning:#> The log-likelihood is getting suspiciously close to 0 and the delta is still large.#> There may be complete separation in the dataset.#> This may result in incorrect inference of coefficients.#> See https://stats.stackexchange.com/q/11109/11867 for more.#> /.../__init__.py:1165: ConvergenceWarning:#> Column x has high sample correlation with the duration column.#> This may harm convergence.#> This could be a form of 'complete separation'.#> See https://stats.stackexchange.com/questions/11109/how-to-deal-with-perfect-separation-in-logistic-regression#> /.../coxph_fitter.py:1611:#> ConvergenceWarning: Newton-Rhaphson failed to converge sufficiently.#> Please see the following tips in the lifelines documentation:#> https://lifelines.readthedocs.io/en/latest/Examples.html#problems-with-convergence-in-the-cox-proportional-hazard-model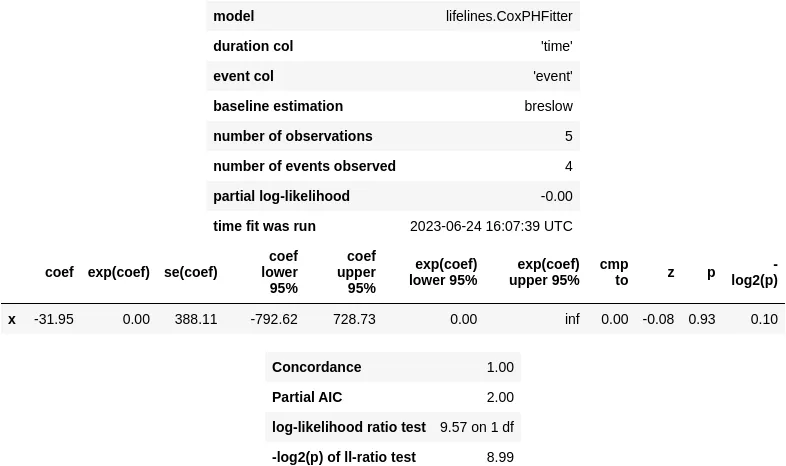

Come accade nella regressione logistica, ci troviamo di fronte a avvisi di convergenza e a intervalli di confidenza estremamente ampi per il nostro coefficiente predittore β . Come risultato, otteniamo un p-value di 0,93 !

Se semplicemente filtriamo i modelli in base ai p-value senza tener conto di questo problema o senza condurre ulteriori indagini, trascureremmo questi predittori perfetti.

Per affrontare questo problema di convergenza, la documentazione della libreria lifelines e alcuni utili thread di StackOverflow suggeriscono una soluzione potenziale: incorporare un termine di regolarizzazione nella funzione di costo. Questo termine aumenta efficacemente il costo per valori di coefficiente grandi, e puoi attivare la regolarizzazione L2 impostando l’argomento penalizer a un valore maggiore di zero:

perfect_pen_cox_model = CoxPHFitter(penalizer=0.01, l1_ratio=0)perfect_pen_cox_model.fit(perfect_df, duration_col='time', event_col='event', formula='x')perfect_pen_cox_model.print_summary()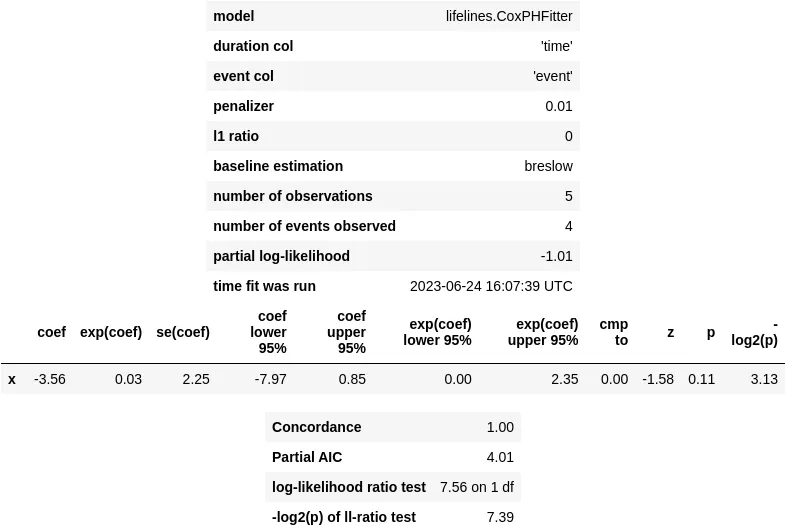

Questo approccio risolve l’avviso di convergenza, ma non riduce significativamente quel fastidioso p-value. Anche con questo trucco di regolarizzazione, il p-value per un predittore perfetto rimane ancora a un valore abbastanza grande di 0,11.

Il tempo è relativo: contano solo i ranghi

Infine, verificheremo che i valori assoluti dei tempi degli eventi non hanno alcun impatto su una regressione di Cox, utilizzando il nostro esempio precedente. Per fare ciò, introdurremo una nuova colonna chiamata time2, che conterrà numeri casuali nello stesso ordine della colonna time:

sample_df = pd.DataFrame({    'subject': ['A', 'B', 'C', 'D', 'E', 'F', 'G', 'H'],    'x': [-1.7, -0.4, 0.0, 0.5, 0.9, 1.2, 1.3, 1.45],    'time': [1, 2, 4, 3, 5, 7, 6, 8],    'rank_x': [1, 2, 3, 4, 5, 6, 7, 8],    'event': [1, 1, 1, 1, 1, 1, 1, 0],}).sort_values('time')np.random.seed(42)sample_df['time2'] = sorted(np.random.randint(low=-42, high=888, size=8))sample_df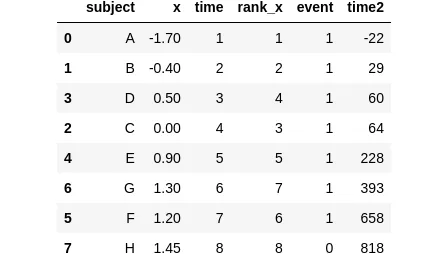

I loro adattamenti sono infatti identici:

sample_cox_model = CoxPHFitter()sample_cox_model.fit(  sample_df,  duration_col='time',  event_col='event',  formula='x')sample_cox_model.print_summary()

sample_cox_model = CoxPHFitter()sample_cox_model.fit(  sample_df,  duration_col='time2',  event_col='event',  formula='x')sample_cox_model.print_summary()

Conclusione

Cosa abbiamo imparato da tutto questo?

• I predittori perfetti nei modelli di sopravvivenza sono quelli i cui ranghi corrispondono perfettamente ai ranghi dei tempi degli eventi.
• La regressione di Cox non può adattare questi predittori perfetti con un coefficiente β finito, portando a intervalli di confidenza ampi e grandi p-value.
• I valori effettivi dei tempi degli eventi non contano davvero, è tutto una questione di ranghi.
• Quando i ranghi dei tempi degli eventi e dei predittori non si allineano, non otteniamo quell’effetto di cancellazione utile per i valori β grandi nelle verosimiglianze. Quindi, abbiamo bisogno di almeno un caso in cui i ranghi non corrispondono per avere un adattamento con un coefficiente finito.
• Anche se proviamo alcune tecniche di regolarizzazione fantasiose, i predittori perfetti possono ancora darci quegli intervalli di confidenza fastidiosamente ampi e i p-value alti in situazioni reali.
• Come nella regressione logistica, se non ci importano davvero quei p-value, l’uso di un metodo di regolarizzazione può comunque fornirci un adattamento del modello utile che ottiene la previsione corretta!

Se vuoi eseguire il codice da solo, sentiti libero di utilizzare i notebook IPython dal mio Github: https://github.com/igor-sb/blog/blob/main/posts/cox_perfect.ipynb

Arrivederci al prossimo post! 👋