Padronare il Monte Carlo Come simulare il tuo percorso verso modelli di apprendimento automatico migliori

Padronare il Monte Carlo simulando il percorso verso modelli di apprendimento automatico migliori

Applicazione di approcci probabilistici mediante l’ottimizzazione di algoritmi predittivi tramite tecniche di simulazione

Come uno scienziato giocando a carte ha cambiato per sempre il gioco delle statistiche

Nell’anno tumultuoso del 1945, mentre il mondo era afferrato dagli spasimi finali della Seconda Guerra Mondiale, una partita di solitario ha silenziosamente scatenato un progresso nel campo del calcolo. Non era una partita ordinaria, ma una che avrebbe portato alla nascita del metodo Monte Carlo(1). Il giocatore? Nient’altro che lo scienziato Stanislaw Ulam, che era anche profondamente impegnato nel Progetto Manhattan(2). Ulam, mentre era convalescente da una malattia, si trovò immerso nel solitario. Le complesse probabilità del gioco lo intrigarono e si rese conto che la simulazione del gioco ripetutamente poteva fornire una buona approssimazione di queste probabilità(3). Fu un momento di illuminazione, simile a quella della mela di Newton, ma con le carte invece che con il frutto. Ulam discusse poi queste idee con il suo collega John von Neumann e insieme formalizzarono il metodo Monte Carlo, chiamato così dal famoso Casinò di Monte Carlo a Monaco, (rappresentato nel famoso dipinto di Edvard Munch mostrato sopra), dove le puntate sono alte e il caso regna sovrano – proprio come il metodo stesso.

Passando al giorno d’oggi, il metodo Monte Carlo è diventato un’arma vincente nel mondo del machine learning, incluso l’utilizzo nell’apprendimento per rinforzo, nel filtraggio bayesiano e nell’ottimizzazione di modelli complessi(4). La sua robustezza e versatilità ne hanno assicurato la continua rilevanza, più di sette decenni dopo la sua creazione. Dai giochi di solitario di Ulam alle sofisticate applicazioni di intelligenza artificiale di oggi, il metodo Monte Carlo rimane una testimonianza del potere della simulazione e dell’approssimazione nel trattare sistemi complessi.

Giocare le tue carte giuste con simulazioni probabilistiche

Nell’intricato mondo della scienza dei dati e del machine learning, le simulazioni Monte Carlo sono simili a una scommessa ben calcolata. Questa tecnica statistica ci permette di piazzare scommesse strategiche di fronte all’incertezza, dando un senso probabilistico a problemi complessi e deterministici. In questo articolo, decifreremo le simulazioni Monte Carlo e ne esploreremo le potenti applicazioni nelle statistiche e nel machine learning.

Inizieremo facendo una disamina approfondita della teoria alla base delle simulazioni Monte Carlo, illustrando i principi che rendono questa tecnica uno strumento potente per la risoluzione dei problemi. Lavoreremo su alcune applicazioni pratiche in Python, dimostrando come le simulazioni Monte Carlo possano essere implementate nella pratica.

• La registrazione KYC ora resa facile usando l’IA
• Una ricerca sull’IA sull’incorporazione dell’interpolazione tra immagini con l’aiuto dei modelli di diffusione
• Stability AI ha rilasciato Beluga 1 e Stable Beluga 2, nuovi LLM open-access.

Successivamente, esploreremo come le simulazioni Monte Carlo possano essere utilizzate per ottimizzare modelli di machine learning. Ci concentreremo sul compito spesso impegnativo dell’ottimizzazione dei parametri, fornendo un set di strumenti pratici per navigare in questo paesaggio complesso.

Quindi, piazza le tue scommesse e cominciamo!

Comprensione delle simulazioni Monte Carlo

Le simulazioni Monte Carlo sono una tecnica preziosa per matematici e scienziati dei dati. Queste simulazioni forniscono una metodologia per navigare attraverso un’ampia e complessa gamma di possibilità, formulando ipotesi educate e raffinando progressivamente le scelte fino a quando non emerge la soluzione più adatta.

Funziona così: generiamo un vasto numero di scenari casuali, seguendo un determinato processo predefinito, quindi analizziamo questi scenari per stimare la probabilità di diversi risultati. Ecco un’analogia per rendere più chiara questa idea: considera ogni scenario come un turno nel popolare gioco da tavolo di Hasbro “Cluedo”. Per coloro che non lo conoscono, “Cluedo” è un gioco in stile detective in cui i giocatori si muovono in una villa raccogliendo prove per dedurre i dettagli di un crimine – chi, cosa e dove. Ogni turno, o domanda fatta, elimina possibili risposte e avvicina i giocatori alla rivelazione del vero scenario del crimine. Allo stesso modo, ogni simulazione in uno studio Monte Carlo fornisce informazioni che ci avvicinano alla soluzione del nostro problema complesso.

Nel campo del machine learning, questi “scenari” possono rappresentare diverse configurazioni del modello, insiemi variati di iperparametri, modi alternativi di suddividere un set di dati in set di addestramento e test e molte altre applicazioni. Valutando i risultati di questi scenari, possiamo ottenere preziose informazioni sul comportamento del nostro algoritmo di machine learning, consentendo decisioni informate sulla sua ottimizzazione.

Un Gioco di Freccette

Per capire le simulazioni di Monte Carlo, immagina di giocare a un gioco di freccette. Ma anziché puntare a un bersaglio specifico, sei bendato e lanci le freccette a caso su una grande freccette quadrata. All’interno di questo quadrato c’è un bersaglio circolare. Il tuo obiettivo è stimare il valore di pi greco, il rapporto tra la circonferenza del cerchio e il suo diametro.

Sembra impossibile, vero? Ma ecco il trucco: il rapporto tra l’area del cerchio e l’area del quadrato è pi greco/4. Quindi, se lanci un gran numero di freccette, il rapporto tra le freccette che atterrano all’interno del cerchio e il numero totale di freccette dovrebbe essere approssimativamente pi greco/4. Moltiplica questo rapporto per 4 e otterrai una stima di pi greco!

Random Guessing vs. Monte Carlo

Per illustrare la potenza delle simulazioni di Monte Carlo, confrontiamola con un metodo più semplice, forse il più semplice di tutti: il random guessing (indovinare a caso).

Quando esegui il codice qui sotto per entrambi i casi (random e Monte Carlo), otterrai un diverso insieme di predizioni ogni volta. Questo è da aspettarsi, perché le freccette vengono lanciate a caso. Questa è una caratteristica chiave delle simulazioni di Monte Carlo: sono per loro natura stocastiche, o casuali. Ma nonostante questa casualità, possono fornire stime molto accurate quando usate correttamente. Quindi, anche se i tuoi risultati non saranno esattamente come i miei, racconteranno la stessa storia.

Nel primo set di visualizzazioni (da Figura 1a a Figura 1f), stiamo facendo una serie di indovinamenti casuali per il valore di pi greco, generando ogni volta un cerchio basato sul valore indovinato. Diamo a questa “casualità” una spinta nella giusta direzione, supponendo che mentre non possiamo ricordare l’esatto valore di pi greco, sappiamo che è superiore a 2 e inferiore a 4. Come puoi vedere dalle figure risultanti, la dimensione del cerchio varia ampiamente a seconda dell’indovinamento, dimostrando l’inaccuratezza di questo approccio (cosa che non dovrebbe sorprendere). Il cerchio verde in ogni figura rappresenta il cerchio unitario, il cerchio “reale” che stiamo cercando di stimare. Il cerchio blu si basa sul nostro indovinamento casuale.

#Indovinamento Casuale di Pi Greco# Prima di eseguire questo codice, assicurati di avere installati i pacchetti necessari.# Puoi installarli usando "pip install" sul tuo terminale o "conda install" se utilizzi un ambiente conda# Importa le librerie necessarieimport randomimport plotly.graph_objects as goimport numpy as np# Numero di indovinamenti da fare. Regola questo valore per fare più indovinamenti e visualizzazioni successivenum_indovinamenti = 6# Genera le coordinate del cerchio unitario# Utilizziamo np.linspace per generare numeri equidistanti nell'intervallo da 0 a 2*pi greco.# Questi rappresentano gli angoli nel cerchio unitario.theta = np.linspace(0, 2*np.pi, 100)# Le coordinate x e y del cerchio unitario sono quindi il coseno e il seno di questi angoli, rispettivamente.cerchio_unitario_x = np.cos(theta)cerchio_unitario_y = np.sin(theta)# Faremo un certo numero di indovinamenti per il valore di pi grecofor i in range(num_indovinamenti):    # Fai un indovinamento casuale per pi greco tra 2 e 4    indovinamento_pi = random.uniform(2, 4)    # Genera le coordinate per il cerchio basato sull'indovinamento    # Il raggio del cerchio è il valore indovinato di pi greco diviso 4.    raggio = indovinamento_pi / 4    # Le coordinate x e y del cerchio sono quindi il raggio moltiplicato per il coseno e il seno degli angoli, rispettivamente.    cerchio_x = raggio * np.cos(theta)    cerchio_y = raggio * np.sin(theta)    # Crea un grafico a dispersione del cerchio    fig = go.Figure()    # Aggiungi il cerchio al grafico    # Utilizziamo una traccia Scatter con modalità 'lines' per disegnare il cerchio.    fig.add_trace(go.Scatter(        x = cerchio_x,        y = cerchio_y,        mode='lines',        line=dict(            color='blue',            width=3        ),        name='Cerchio Stimato'    ))    # Aggiungi il cerchio unitario al grafico    fig.add_trace(go.Scatter(        x = cerchio_unitario_x,        y = cerchio_unitario_y,        mode='lines',        line=dict(            color='green',            width=3        ),        name='Cerchio Unitario'    ))    # Aggiorna il layout del grafico    # Impostiamo il titolo per includere il valore indovinato di pi greco e regoliamo la dimensione e gli intervalli degli assi per visualizzare correttamente i cerchi.    fig.update_layout(        title=f"Fig1{chr(97 + i)}: Indovinamento Casuale di Pi Greco: {indovinamento_pi}",        width=600,        height=600,        xaxis=dict(            constrain="domain",            range=[-1, 1]        ),        yaxis=dict(            scaleanchor="x",            scaleratio=1,            range=[-1, 1]        )    )    # Mostra i grafici    fig.show()

Potresti notare qualcosa di strano: nel metodo di indovinare casualmente, a volte un’ipotesi più vicina al valore reale di pi produce un cerchio più lontano dal cerchio unitario. Questa apparente contraddizione si verifica perché stiamo guardando la circonferenza dei cerchi, non il loro raggio o area. La differenza visiva tra i due cerchi rappresenta l’errore nella stima della circonferenza del cerchio in base all’ipotesi, non l’intero cerchio.

Nel secondo set di visualizzazioni (Figura 2a a Figura 2f), stiamo utilizzando il metodo di Monte Carlo per stimare il valore di pi. Invece di fare una congettura casuale, stiamo lanciando un gran numero di freccette su un quadrato e contando quante cadono all’interno di un cerchio inscritto nel quadrato. La stima risultante di pi è molto più accurata, come si può vedere dalle figure in cui la dimensione del cerchio è molto più vicina al cerchio unitario effettivo. I punti verdi rappresentano le freccette che sono cadute all’interno del cerchio unitario, mentre i punti rossi rappresentano le freccette che sono cadute all’esterno.

#Stima di Monte Carlo di Pi# Importiamo le librerie necessarieimport randomimport mathimport plotly.graph_objects as goimport plotly.io as pioimport numpy as np# Simuleremo il lancio delle freccette su una tabella da dart per stimare pi. Lanciamo 10.000 freccette.num_frecce = 10000# Per tenere traccia delle frecce che cadono nel cerchio.frecce_in_cerchio = 0# Memorizzeremo le coordinate delle frecce che cadono all'interno e all'esterno del cerchio.x_coords_in, y_coords_in, x_coords_out, y_coords_out = [], [], [], []# Generiamo 6 figure durante la simulazione. Pertanto, creeremo una nuova figura ogni 1.666 frecce (10.000 diviso per 6).num_figure = 6frecce_per_figura = num_frecce // num_figure# Creiamo un cerchio unitario per confrontare le nostre stime. Qui, usiamo coordinate polari e convertiamo in coordinate cartesiane.theta = np.linspace(0, 2*np.pi, 100)unit_circle_x = np.cos(theta)unit_circle_y = np.sin(theta)# Iniziamo a lanciare le frecce (simulando punti casuali all'interno di un quadrato 1x1 e verificando se cadono all'interno di un quarto di cerchio).for i in range(num_frecce):    # Generiamo coordinate x, y casuali tra -1 e 1.    x, y = random.uniform(-1, 1), random.uniform(-1, 1)        # Se una freccia (punto) è più vicina all'origine (0,0) rispetto alla distanza di 1, è all'interno del cerchio.    if math.sqrt(x**2 + y**2) <= 1:        frecce_in_cerchio += 1        x_coords_in.append(x)        y_coords_in.append(y)    else:        x_coords_out.append(x)        y_coords_out.append(y)    # Dopo ogni 1.666 frecce, vediamo come appare la nostra stima rispetto al vero cerchio unitario.    if (i + 1) % frecce_per_figura == 0:        # Stimiamo pi osservando la proporzione di frecce che sono cadute nel cerchio (rispetto al numero totale di frecce).        stima_pi = 4 * frecce_in_cerchio / (i + 1)        # Ora creiamo un cerchio dalla nostra stima per confrontare visualmente con il cerchio unitario.        raggio_cerchio_stimato = stima_pi / 4        cerchio_stimato_x = raggio_cerchio_stimato * np.cos(theta)        cerchio_stimato_y = raggio_cerchio_stimato * np.sin(theta)        # Tracciamo i risultati usando Plotly.        fig = go.Figure()        # Aggiungiamo le frecce che sono cadute all'interno e all'esterno del cerchio al grafico.        fig.add_trace(go.Scattergl(x=x_coords_in, y=y_coords_in, mode='markers', name='Frecce all\'interno del cerchio', marker=dict(color='green', size=4, opacity=0.8)))        fig.add_trace(go.Scattergl(x=x_coords_out, y=y_coords_out, mode='markers', name='Frecce all\'esterno del cerchio', marker=dict(color='red', size=4, opacity=0.8)))        # Aggiungiamo il vero cerchio unitario e il nostro cerchio stimato al grafico.        fig.add_trace(go.Scatter(x=unit_circle_x, y=unit_circle_y, mode='lines', name='Cerchio unitario', line=dict(color='green', width=3)))        fig.add_trace(go.Scatter(x=cerchio_stimato_x, y=cerchio_stimato_y, mode='lines', name='Cerchio stimato', line=dict(color='blue', width=3)))        # Personalizziamo il layout del grafico.        fig.update_layout(title=f"Figura {chr(97 + (i + 1) // frecce_per_figura - 1)}: Frecce lanciate: {(i + 1)}, Stima di Pi: {stima_pi}", width=600, height=600, xaxis=dict(constrain="domain", range=[-1, 1]), yaxis=dict(scaleanchor="x", scaleratio=1, range=[-1, 1]), legend=dict(yanchor="top", y=0.99, xanchor="left", x=0.01))        # Mostrare il grafico.        fig.show()        # Salvare il grafico come file immagine PNG.        pio.write_image(fig, f"fig2{chr(97 + (i + 1) // frecce_per_figura - 1)}.png")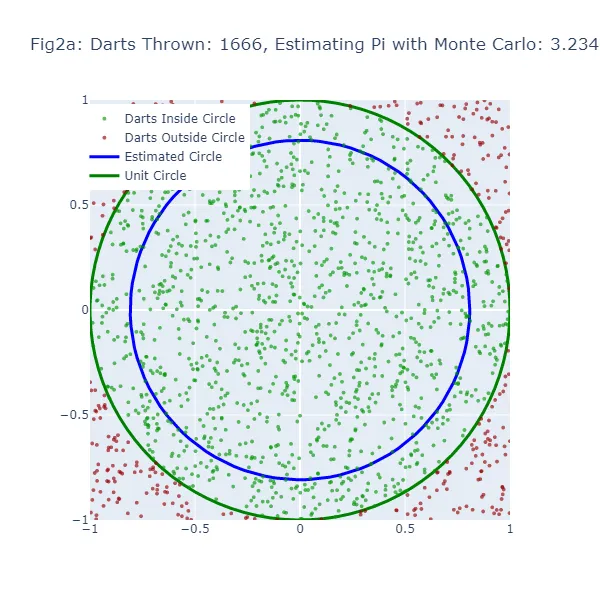

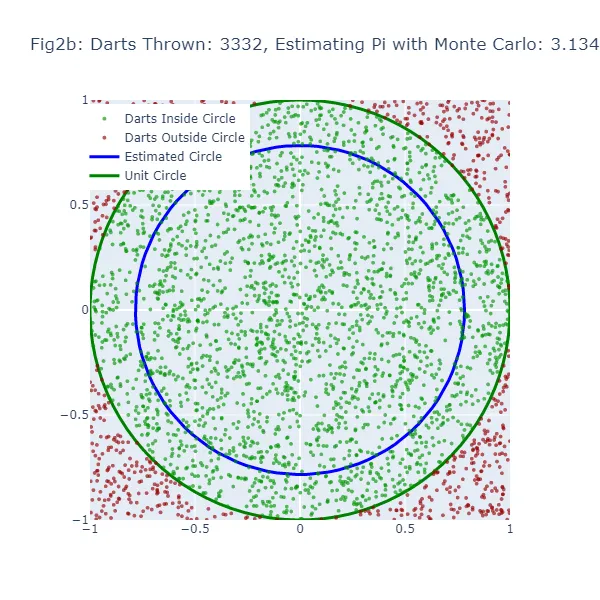
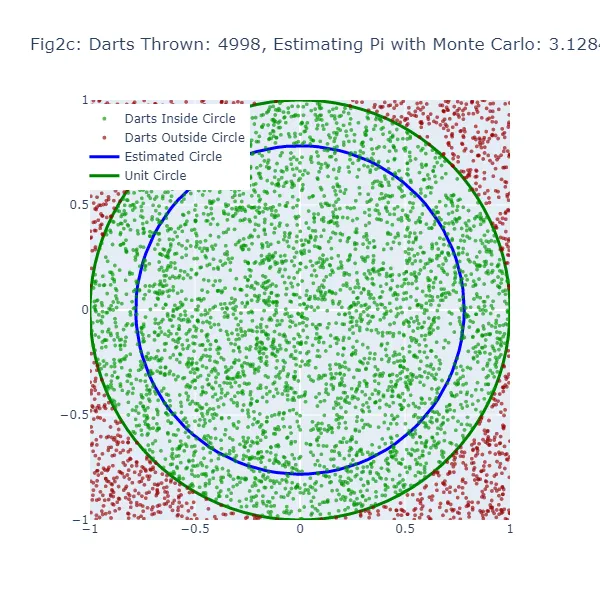
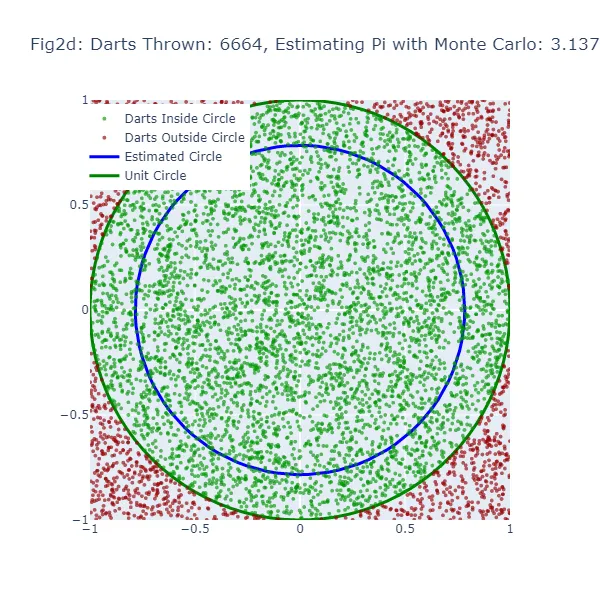
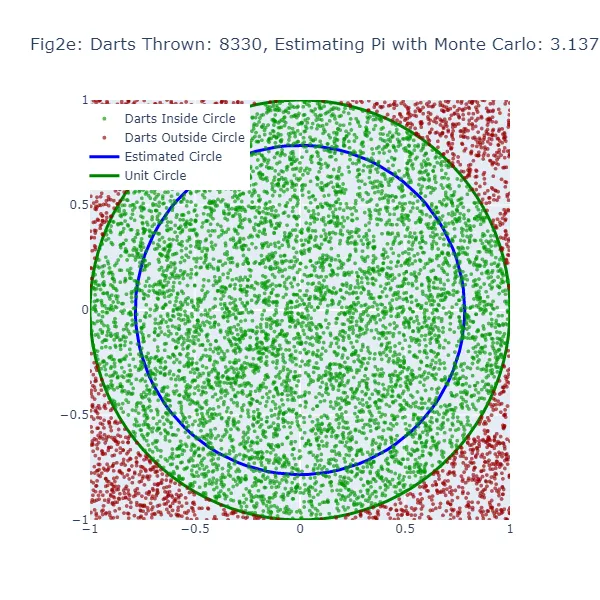
Nel metodo di Monte Carlo, la stima di pi è basata sulla proporzione di “dardi” che cadono all’interno del cerchio rispetto al numero totale di dardi lanciati. Il valore stimato di pi risultante viene utilizzato per generare un cerchio. Se la stima di Monte Carlo è inaccurata, il cerchio sarà nuovamente di dimensioni errate. La larghezza dello spazio tra questo cerchio stimato e il cerchio unitario fornisce un’indicazione dell’accuratezza della stima di Monte Carlo.

Tuttavia, poiché il metodo di Monte Carlo genera stime più accurate man mano che aumenta il numero di “dardi”, il cerchio stimato dovrebbe convergere verso il cerchio unitario man mano che vengono lanciati più “dardi”. Pertanto, mentre entrambi i metodi mostrano uno spazio vuoto quando la stima è inaccurata, questo spazio dovrebbe diminuire più costantemente con il metodo di Monte Carlo man mano che aumenta il numero di “dardi” lanciati.

Prevedere Pi: Il Potere della Probabilità

Ciò che rende le simulazioni di Monte Carlo così potenti è la loro capacità di sfruttare la casualità per risolvere problemi deterministici. Generando un gran numero di scenari casuali e analizzando i risultati, possiamo stimare la probabilità di diversi risultati, anche per problemi complessi che sarebbero difficili da risolvere analiticamente.

Nel caso della stima di pi, il metodo di Monte Carlo ci consente di fare una stima molto accurata, anche se stiamo semplicemente lanciando dardi casualmente. Come discusso, più dardi lanciamo, più accurata diventa la nostra stima. Questo è una dimostrazione della legge dei grandi numeri, un concetto fondamentale nella teoria della probabilità che afferma che la media dei risultati ottenuti da un gran numero di prove dovrebbe essere vicina al valore atteso e tenderà a diventare sempre più vicina man mano che vengono effettuate più prove. Vediamo se questo tende ad essere vero per i nostri sei esempi mostrati in Figure 2a-2f tracciando il numero di dardi lanciati rispetto alla differenza tra la stima di pi stimata con Monte Carlo e il vero valore di pi. In generale, il nostro grafico (Figure 2g) dovrebbe avere una tendenza negativa. Ecco il codice per realizzare questo:

# Calcola le differenze tra il vero pi e la stima di pidiff_pi = [abs(estimate - math.pi) for estimate in pi_estimates]# Crea il grafico per il numero di dardi e la differenza in pi (Figure 2g)fig2g = go.Figure(data=go.Scatter(x=num_darts_thrown, y=diff_pi, mode='lines'))# Aggiungi titolo ed etichette al graficofig2g.update_layout(    title="Fig2g: Dardi Lanciati vs Differenza nella Stima di Pi",    xaxis_title="Numero di Dardi Lanciati",    yaxis_title="Differenza in Pi",)# Mostra il graficofig2g.show()# Salva il grafico come pngpio.write_image(fig2g, "fig2g.png")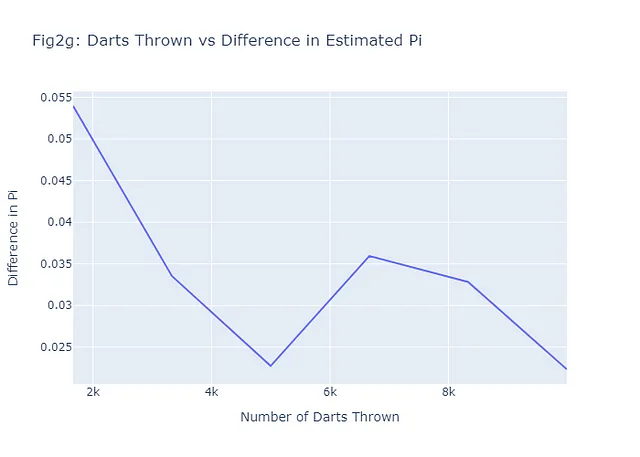

Si noti che, anche con solo 6 esempi, il pattern generale è come previsto: più dardi vengono lanciati (più scenari), una differenza più piccola tra il valore stimato e il valore reale, e quindi una migliore previsione.

Diciamo che lanciamo in totale 1.000.000 di freccette e ci concediamo 500 previsioni. In altre parole, registreremo la differenza tra i valori stimati e reali di pi in 500 intervalli equidistanti durante la simulazione di 1.000.000 di freccette lanciate. Invece di generare 500 figure extra, passiamo direttamente a ciò che stiamo cercando di confermare: se è davvero vero che più freccette vengono lanciate, la differenza tra il nostro valore previsto di pi e il vero pi diminuisce. Utilizzeremo un grafico a dispersione (Figura 2h):

#500 scenari Monte Carlo; 1.000.000 di freccette lanciateimport randomimport mathimport plotly.graph_objects as goimport numpy as np# Numero totale di freccette da lanciare (1M)num_frecce = 1000000frecce_in_cerchio = 0# Numero di scenari da registrare (500)num_scenari = 500frecce_per_scenario = num_frecce // num_scenari# Liste per memorizzare i dati di ogni scenariolista_frecce_lanciate = []lista_diff_pi = []# Lanciamo un certo numero di freccefor i in range(num_frecce):    # Generiamo coordinate casuali x, y tra -1 e 1    x, y = random.uniform(-1, 1), random.uniform(-1, 1)        # Verifichiamo se la freccetta è all'interno del cerchio    # Una freccetta è all'interno del cerchio se la distanza dall'origine (0,0) è minore o uguale a 1    if math.sqrt(x**2 + y**2) <= 1:        frecce_in_cerchio += 1    # Se è il momento di registrare uno scenario    if (i + 1) % frecce_per_scenario == 0:        # Stimiamo pi con il metodo Monte Carlo        # La stima è 4 volte il numero di frecce nel cerchio diviso per il numero totale di frecce        stima_pi = 4 * frecce_in_cerchio / (i + 1)        # Registriamo il numero di frecce lanciate e la differenza tra i valori stimati e reali di pi        lista_frecce_lanciate.append((i + 1) / 1000)  # Dividiamo per 1000 per visualizzare in migliaia        lista_diff_pi.append(abs(stima_pi - math.pi))# Creiamo un grafico a dispersione dei datifig = go.Figure(data=go.Scattergl(x=lista_frecce_lanciate, y=lista_diff_pi, mode='markers'))# Aggiorniamo il layout del graficofig.update_layout(    title="Fig2h: Differenza tra Pi Stimato e Pi Reale vs. Numero di Frecce Lanciate (in migliaia)",    xaxis_title="Numero di Frecce Lanciate (in migliaia)",    yaxis_title="Differenza tra Pi Stimato e Pi Reale",)# Mostrare il graficofig.show()# Salvare il grafico come pngpio.write_image(fig2h, "fig2h.png")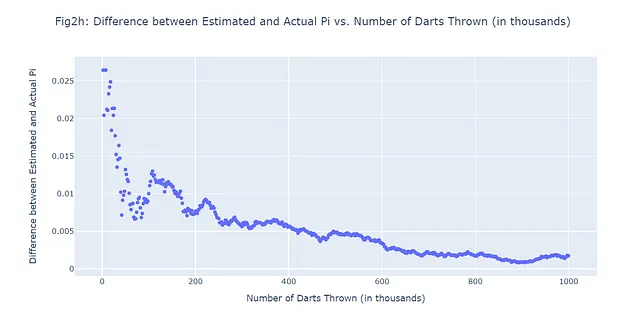

Simulazioni di Monte Carlo e Ottimizzazione degli Iperparametri: Una Combinazione Vincente

Potresti pensare a questo punto: “Monte Carlo è uno strumento statistico interessante, ma come si applica all’apprendimento automatico?” La risposta breve è: in molti modi. Una delle molte applicazioni delle simulazioni di Monte Carlo nell’apprendimento automatico è nel campo dell’ottimizzazione degli iperparametri.

Gli iperparametri sono le manopole e le rotelle che noi (gli esseri umani) regoliamo quando configuriamo gli algoritmi di apprendimento automatico. Controllano aspetti del comportamento dell’algoritmo che, fondamentalmente, non vengono appresi dai dati. Ad esempio, in un albero decisionale, la profondità massima dell’albero è un iperparametro. In una rete neurale, il tasso di apprendimento e il numero di strati nascosti sono iperparametri.

Scegliere i giusti iperparametri può fare la differenza tra un modello che si comporta male e uno che si comporta in modo eccellente. Ma come sappiamo quali iperparametri scegliere? Qui entrano in gioco le simulazioni di Monte Carlo.

Tradizionalmente, i praticanti di apprendimento automatico hanno utilizzato metodi come la ricerca a griglia o la ricerca casuale per ottimizzare gli iperparametri. Questi metodi prevedono la specifica di un insieme di valori possibili per ciascun iperparametro, quindi l’addestramento e la valutazione di un modello per ogni possibile combinazione di iperparametri. Questo può essere computazionalmente costoso e richiedere molto tempo, specialmente quando ci sono molti iperparametri da ottimizzare o un’ampia gamma di valori possibili che ognuno può assumere.

Le simulazioni di Monte Carlo offrono un’alternativa più efficiente. Invece di cercare esaustivamente tutte le possibili combinazioni di iperparametri, possiamo campionare casualmente lo spazio degli iperparametri secondo una qualche distribuzione di probabilità. Questo ci consente di esplorare lo spazio degli iperparametri in modo più efficiente e trovare combinazioni buone di iperparametri più velocemente.

Nella prossima sezione, useremo un dataset reale per dimostrare come utilizzare le simulazioni di Monte Carlo per l’ottimizzazione degli iperparametri nella pratica. Cominciamo!

Simulazioni di Monte Carlo per l’Ottimizzazione degli Iperparametri

Il Battito Cardiaco del Nostro Esperimento: Il Dataset delle Malattie Cardiache

Nel mondo del machine learning, i dati sono il sangue vitale che alimenta i nostri modelli. Per la nostra esplorazione delle simulazioni di Monte Carlo nell’ottimizzazione degli iperparametri, esaminiamo un dataset che è vicino al cuore – letteralmente. Il dataset delle Malattie Cardiache (CC BY 4.0) dell’UCI Machine Learning Repository è una collezione di cartelle cliniche di pazienti, alcuni dei quali hanno una malattia cardiaca.

Il dataset contiene 14 attributi, tra cui età, sesso, tipo di dolore al petto, pressione sanguigna a riposo, livelli di colesterolo, glicemia a digiuno e altri. La variabile target è la presenza di malattie cardiache, rendendo questa una classificazione binaria. Con una combinazione di caratteristiche categoriche e numeriche, è un dataset interessante per dimostrare l’ottimizzazione degli iperparametri.

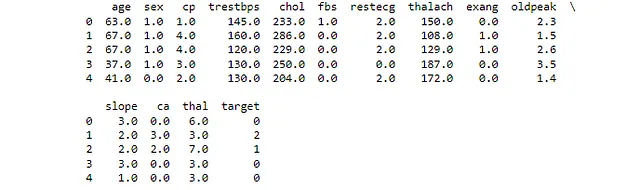
Prima di tutto, diamo un’occhiata al nostro dataset per avere un’idea di ciò con cui lavoreremo – sempre un buon punto di partenza.

#Carica e visualizza le prime righe del dataset# Importa le librerie necessarieimport pandas as pdfrom sklearn.model_selection import train_test_splitfrom sklearn.preprocessing import StandardScaler, OneHotEncoderfrom sklearn.compose import ColumnTransformerfrom sklearn.pipeline import Pipelinefrom sklearn.linear_model import LogisticRegressionfrom sklearn.model_selection import GridSearchCVfrom sklearn.metrics import roc_auc_scoreimport numpy as npimport plotly.graph_objects as go# Carica il dataset# Il dataset è disponibile presso l'UCI Machine Learning Repository# È un dataset sulle malattie cardiache e include diverse misurazioni dei pazientiurl = "https://archive.ics.uci.edu/ml/machine-learning-databases/heart-disease/processed.cleveland.data"# Definisci i nomi delle colonne per il dataframecolumn_names = ["età", "sesso", "cp", "trestbps", "chol", "glicemia", "ecg", "thalach", "exang", "depressione", "slope", "ca", "thal", "target"]# Carica il dataset in un dataframe pandas# Specifichiamo i nomi delle colonne e diciamo anche a pandas di trattare '?' come NaN df = pd.read_csv(url, names=column_names, na_values="?")# Stampa le prime righe del dataframe# Ciò ci dà una rapida panoramica dei datiprint(df.head())

Questo ci mostra i primi quattro valori nel nostro dataset per tutte le colonne. Se hai caricato il csv corretto e hai nominato le colonne come ho fatto io, il tuo output assomiglierà a Figura 3.

Impostare il Polso: Preprocessare i Dati

Prima di poter utilizzare il dataset delle Malattie Cardiache per l’ottimizzazione degli iperparametri, dobbiamo preprocessare i dati. Questo comporta diversi passaggi:

1. Gestione dei valori mancanti: Alcuni record nel dataset hanno valori mancanti. Dovremo decidere come gestirli, se eliminare i record, riempire i valori mancanti o utilizzare qualche altro metodo.
2. Codifica delle variabili categoriche: Molti algoritmi di machine learning richiedono che i dati di input siano numerici. Dovremo convertire le variabili categoriche in un formato numerico.
3. Normalizzazione delle caratteristiche numeriche: Gli algoritmi di machine learning spesso funzionano meglio quando le caratteristiche numeriche si trovano su una scala simile. Applicheremo la normalizzazione per adattare la scala di queste caratteristiche.

Iniziamo gestendo i valori mancanti. Nel nostro dataset delle Malattie Cardiache, abbiamo alcuni valori mancanti nelle colonne ‘ca’ e ‘thal’. Riempiremo questi valori mancanti con la mediana della rispettiva colonna. Questa è una strategia comune per gestire i dati mancanti, poiché non influisce drasticamente sulla distribuzione dei dati.

Successivamente, codificheremo le variabili categoriche. Nel nostro dataset, le colonne ‘cp’, ‘ecg’, ‘slope’, ‘ca’ e ‘thal’ sono categoriche. Utilizzeremo la codifica di etichetta per convertire queste variabili categoriche in numeriche. La codifica di etichetta assegna a ogni categoria univoca in una colonna un diverso intero.

Infine, normalizzeremo le caratteristiche numeriche. La normalizzazione regola la scala delle caratteristiche numeriche in modo che rientrino tutte in un’intervallo simile. Questo può aiutare a migliorare le prestazioni di molti algoritmi di machine learning. Utilizzeremo la standardizzazione per la normalizzazione, che trasforma i dati in modo che abbiano una media di 0 e una deviazione standard di 1.

Ecco il codice Python che esegue tutte queste operazioni di preprocessing:

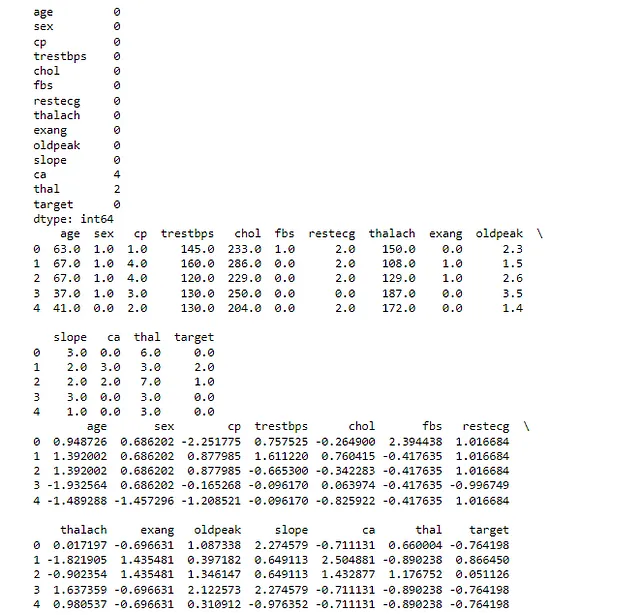
# Preprocess# Importare le librerie necessariefrom sklearn.impute import SimpleImputerfrom sklearn.preprocessing import LabelEncoder# Identificare i valori mancanti nel dataset# Questo stamperà il numero di valori mancanti in ogni colonnaprint(df.isnull().sum())# Riempi i valori mancanti con la mediana della colonna# La classe SimpleImputer di sklearn fornisce strategie di base per l'imputazione dei valori mancanti# Stiamo usando la strategia 'mediana', che sostituisce i valori mancanti con la mediana di ogni colonnaimputer = SimpleImputer(strategy='mediana')# Applica l'imputer al dataframe# Il risultato è un nuovo dataframe in cui i valori mancanti sono stati riempitiindf_filled = pd.DataFrame(imputer.fit_transform(df), columns=df.columns)# Stampa le prime righe del dataframe riempito# Questo ci dà un controllo rapido per verificare che l'imputazione sia stata eseguita correttamentestampa(df_filled.head())# Identifica le variabili categoriche nel dataset# Queste sono variabili che contengono dati non numericivariabili_categoriche = df_filled.select_dtypes(include='object').columns# Codifica le variabili categoriche# La classe LabelEncoder di sklearn converte ogni stringa univoca in un intero univocoencoder = LabelEncoder()for var in variabili_categoriche:    df_filled[var] = encoder.fit_transform(df_filled[var])# Normalizza le caratteristiche numeriche# La classe StandardScaler di sklearn standardizza le caratteristiche rimuovendo la media e ridimensionandole per avere varianze unitariescaler = StandardScaler()# Applica il ridimensionamento al dataframe# Il risultato è un nuovo dataframe in cui le caratteristiche numeriche sono state normalizzatedf_normalized = pd.DataFrame(scaler.fit_transform(df_filled), columns=df_filled.columns)# Stampa le prime righe del dataframe normalizzato# Questo ci dà un controllo rapido per verificare che la normalizzazione sia stata eseguita correttamentestampa(df_normalized.head())

La prima istruzione di stampa ci mostra il numero di valori mancanti in ogni colonna del dataset originale. Nel nostro caso, le colonne ‘ca’ e ‘thal’ avevano alcuni valori mancanti.

La seconda istruzione di stampa ci mostra le prime righe del dataset dopo aver riempito i valori mancanti. Come discusso, abbiamo utilizzato la mediana di ogni colonna per riempire i valori mancanti.

La terza istruzione di stampa ci mostra le prime righe del dataset dopo aver codificato le variabili categoriche. Dopo questo passaggio, tutte le variabili nel nostro dataset sono numeriche.

L’ultima istruzione di stampa ci mostra le prime righe del dataset dopo aver normalizzato le caratteristiche numeriche, in cui i dati avranno una media di 0 e una deviazione standard di 1. Dopo questo passaggio, tutte le caratteristiche numeriche nel nostro dataset hanno una scala simile. Verifica che il tuo output assomigli a Figura 4:

Dopo aver eseguito questo codice, abbiamo un dataset preprocessato pronto per la modellazione.

Implementazione di un modello di apprendimento automatico di base

Ora che abbiamo preprocessato i nostri dati, siamo pronti per implementare un modello di apprendimento automatico di base. Questo servirà come nostro modello di base, che cercheremo in seguito di migliorare attraverso l’ottimizzazione degli iperparametri.

Utilizzeremo un semplice modello di regressione logistica per questa attività. Nota che nonostante sia chiamato “regressione”, questo è in realtà uno degli algoritmi più popolari per problemi di classificazione binaria, come quello con cui stiamo lavorando nel dataset delle malattie cardiache. È un modello lineare che predice la probabilità della classe positiva.

Dopo aver addestrato il nostro modello, valuteremo le sue prestazioni utilizzando due metriche comuni: accuratezza e ROC-AUC. L’accuratezza è la proporzione di previsioni corrette su tutte le previsioni, mentre la ROC-AUC (Receiver Operating Characteristic – Area Under Curve) misura il compromesso tra il tasso di veri positivi e il tasso di falsi positivi.

Ma cosa c’entra tutto questo con le simulazioni di Monte Carlo? Beh, i modelli di apprendimento automatico come la regressione logistica hanno diversi iperparametri che possono essere regolati per migliorare le prestazioni. Tuttavia, trovare il miglior insieme di iperparametri può essere come cercare un ago in un pagliaio. Ecco dove entrano in gioco le simulazioni di Monte Carlo. Campionando casualmente diversi insiemi di iperparametri e valutandone le prestazioni, possiamo stimare la distribuzione di probabilità dei buoni iperparametri e fare una congettura educata sui migliori da utilizzare, in modo simile a come abbiamo scelto valori migliori di π nel nostro esercizio di lancio del dardo.

Ecco il codice Python che implementa e valuta un modello di regressione logistica di base per i nostri dati appena preprocessati:

# Modello di regressione logistica - Baseline# Importare le librerie necessariefrom sklearn.model_selection import train_test_splitfrom sklearn.linear_model import LogisticRegressionfrom sklearn.metrics import accuracy_score, roc_auc_score# Sostituire la colonna 'target' nel DataFrame normalizzato con la colonna 'target' originale# Questo è fatto perché la colonna 'target' originale è stata anch'essa normalizzata, il che non è ciò che vogliamodf_normalized['target'] = df['target']# Binarizzare la colonna 'target'# Questo è fatto perché la colonna 'target' originale contiene valori da 0 a 4# Vogliamo semplificare il problema a un problema di classificazione binaria: malattia cardiaca o nessuna malattia cardiacadf_normalized['target'] = df_normalized['target'].apply(lambda x: 1 if x > 0 else 0)# Dividere i dati in set di addestramento e di test# La colonna 'target' è la nostra etichetta, quindi la rimuoviamo dalle nostre caratteristiche (X)# Utilizziamo una dimensione del test del 20%, il che significa che l'80% dei dati verrà utilizzato per l'addestramento e il 20% per il testX = df_normalized.drop('target', axis=1)y = df_normalized['target']X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)# Implementare un modello di regressione logistica di base# La regressione logistica è un modello lineare semplice ma potente per problemi di classificazione binariamodello = LogisticRegression()modello.fit(X_train, y_train)# Fare previsioni sul set di test# Il modello è stato addestrato, quindi possiamo ora usarlo per fare previsioni su dati non vistiy_pred = modello.predict(X_test)# Valutare il modello# Utilizziamo l'accuratezza (la proporzione di previsioni corrette) e la ROC-AUC (una misura di quanto bene il modello distingue tra le classi) come metricheaccuratezza = accuracy_score(y_test, y_pred)roc_auc = roc_auc_score(y_test, y_pred)# Stampare le metriche di prestazione# Queste ci danno un'indicazione di quanto bene il nostro modello sta performandoprint("Modello di base " + f'Accuratezza: {accuratezza}')print("Modello di base " + f'ROC-AUC: {roc_auc}')

Con un’accuratezza del 0,885 e un punteggio ROC-AUC del 0,884, il nostro modello di regressione logistica di base ha stabilito una solida base su cui migliorare. Queste metriche indicano che il nostro modello si sta comportando molto bene nel distinguere tra pazienti con e senza malattie cardiache. Vediamo se possiamo migliorarlo.

Tuning degli iperparametri con la ricerca a griglia

Nell’apprendimento automatico, le prestazioni di un modello possono spesso essere migliorate regolando i suoi iperparametri. Gli iperparametri sono parametri che non vengono appresi dai dati, ma vengono impostati prima dell’inizio del processo di apprendimento. Ad esempio, nella regressione logistica, la forza di regolarizzazione ‘C’ e il tipo di penalizzazione ‘l1’ o ‘l2’ sono iperparametri.

Eseguiamo la regolazione degli iperparametri sul nostro modello di regressione logistica utilizzando la ricerca a griglia. Regoleremo gli iperparametri ‘C’ e ‘penalty’ e utilizzeremo il punteggio ROC-AUC come metrica di valutazione. Vediamo se possiamo superare le prestazioni del nostro modello di base.

Ora, iniziamo con il codice Python per questa sezione.

# Ricerca a griglia# Importa le librerie necessariefrom sklearn.model_selection import GridSearchCV# Definisci gli iperparametri e i loro valori# 'C' è l'inverso della forza di regolarizzazione (valori più piccoli indicano una regolarizzazione più forte)# 'penalty' specifica la norma utilizzata nella penalizzazione (l1 o l2)iperparametri = {'C': [0,001, 0,01, 0,1, 1, 10, 100, 1000], 'penalty': ['l1', 'l2']}# Implementa la ricerca a griglia# GridSearchCV è un metodo utilizzato per regolare gli iperparametri del nostro modello# Passiamo il nostro modello, gli iperparametri da regolare e il numero di fold per la cross-validation# Utilizziamo il punteggio ROC-AUC come metrica di valutazionericerca_griglia = GridSearchCV(LogisticRegression(), iperparametri, cv=5, scoring='roc_auc')ricerca_griglia.fit(X_train, y_train)# Ottieni i migliori iperparametri# GridSearchCV ha trovato i migliori iperparametri per il nostro modello, quindi li stampiamo migliori_parametri = ricerca_griglia.best_params_stampa(f'Migliori iperparametri: {migliori_parametri}')# Valuta il miglior modello# GridSearchCV ci fornisce anche il miglior modello, quindi possiamo usarlo per fare previsioni e valutare le sue prestazionimiglior_modello = ricerca_griglia.best_estimator_y_pred_migliori = miglior_modello.predict(X_test)accuratezza_migliore = accuracy_score(y_test, y_pred_migliori)roc_auc_migliore = roc_auc_score(y_test, y_pred_migliori)# Stampa le metriche di prestazione del miglior modello# Queste ci danno un'indicazione di quanto bene si sta comportando il nostro modello dopo la regolazione degli iperparametriprint("Metodo della ricerca a griglia " + f'Accuratezza del miglior modello: {accuratezza_migliore}')print("Metodo della ricerca a griglia " + f'ROC-AUC del miglior modello: {roc_auc_migliore}')

Con i migliori iperparametri trovati essere {‘C’: 0,1, ‘penalty’: ‘l2’}, la nostra ricerca a griglia ha un’accuratezza del 0,852 e un punteggio ROC-AUC del 0,853 per il miglior modello. Interessante notare che queste prestazioni sono leggermente inferiori rispetto al nostro modello di base. Ciò potrebbe essere dovuto al fatto che gli iperparametri del nostro modello di base erano già adatti a questo particolare set di dati, oppure potrebbe essere il risultato della casualità intrinseca della divisione tra training e test. Indipendentemente da ciò, è un prezioso promemoria che modelli e tecniche più complessi non sono sempre migliori.

Tuttavia, potreste aver notato che la nostra ricerca a griglia ha esplorato solo un numero relativamente ridotto di possibili combinazioni di iperparametri. In pratica, il numero di iperparametri e i loro valori potenziali possono essere molto più numerosi, rendendo la ricerca a griglia computazionalmente costosa o addirittura impraticabile.

Qui entra in gioco il metodo Monte Carlo. Vediamo se questo approccio più guidato migliora le prestazioni del modello di base originale o del modello basato sulla ricerca a griglia:

#Monte Carlo# Importa le librerie necessariefrom sklearn.metrics import accuracy_score, roc_auc_scorefrom sklearn.linear_model import LogisticRegressionfrom sklearn.model_selection import train_test_splitimport numpy as np# Dividi i dati in set di addestramento e testX_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0,2, random_state=42)# Definisci l'intervallo degli iperparametri# 'C' è l'inverso della forza di regolarizzazione (valori più piccoli indicano una regolarizzazione più forte)# 'penalty' specifica la norma utilizzata nella penalizzazione (l1 o l2)C_range = np.logspace(-3, 3, 7)penalty_options = ['l1', 'l2']# Inizializza le variabili per memorizzare il miglior punteggio e gli iperparametri migliorimiglior_punteggio = 0migliori_iperparametri = None# Esegui la simulazione Monte Carlo# Eseguiremo 1000 iterazioni. Puoi giocare con questo numero per vedere come cambiano le prestazioni.# Ricorda la legge dei grandi numeri!for _ in range(1000):         # Seleziona casualmente gli iperparametri dall'intervallo definito    C = np.random.choice(C_range)    penalty = np.random.choice(penalty_options)        # Crea e valuta il modello con questi iperparametri    # Utilizziamo il solver 'liblinear' in quanto supporta sia la regolarizzazione L1 che L2    modello = LogisticRegression(C=C, penalty=penalty, solver='liblinear')    modello.fit(X_train, y_train)    y_pred = modello.predict(X_test)        # Calcola l'accuratezza e ROC-AUC    accuratezza = accuracy_score(y_test, y_pred)    roc_auc = roc_auc_score(y_test, y_pred)        # Se il ROC-AUC di questo modello è il migliore fino ad ora, memorizza il suo punteggio e gli iperparametri    if roc_auc > miglior_punteggio:        miglior_punteggio = roc_auc        migliori_iperparametri = {'C': C, 'penalty': penalty}# Stampa il miglior punteggio e gli iperparametristampa("Metodo Monte Carlo " + f'Best ROC-AUC: {miglior_punteggio}')stampa("Metodo Monte Carlo " + f'Migliori iperparametri: {migliori_iperparametri}')# Addestra il modello con i migliori iperparametrimiglior_modello = LogisticRegression(**migliori_iperparametri, solver='liblinear')miglior_modello.fit(X_train, y_train)# Effettua previsioni sul set di testy_pred = miglior_modello.predict(X_test)# Calcola e stampa l'accuratezza del miglior modelloaccuratezza = accuracy_score(y_test, y_pred)stampa("Metodo Monte Carlo " + f'Accuratezza del miglior modello: {accuratezza}')

Nel metodo Monte Carlo, abbiamo trovato che il miglior punteggio ROC-AUC era 0,9014, con i migliori iperparametri che erano {‘C’: 0.1, ‘penalty’: ‘l1’}. L’accuratezza del miglior modello era 0,9016.

Sembra che Monte Carlo abbia appena estratto un asso dal mazzo – questo è un miglioramento sia rispetto al modello di base che al modello ottimizzato usando la ricerca in griglia. Ti incoraggio a modificare il codice Python per vedere come influenza le prestazioni, ricordando i principi discussi. Vedi se puoi migliorare il metodo di ricerca in griglia aumentando lo spazio degli iperparametri o confronta il tempo di calcolo con il metodo Monte Carlo. Aumenta e diminuisci il numero di iterazioni per il nostro metodo Monte Carlo per vedere come influisce sulle prestazioni.

Conclusioni

Il metodo Monte Carlo, nato da un gioco di solitario, ha senza dubbio riformato il panorama della matematica computazionale e della scienza dei dati. La sua potenza risiede nella sua semplicità e versatilità, che ci permette di affrontare problemi complessi e ad alta dimensionalità con relativa facilità. Dalla stima del valore di pi con un gioco di freccette all’ottimizzazione degli iperparametri nei modelli di apprendimento automatico, le simulazioni Monte Carlo si sono dimostrate uno strumento prezioso nel nostro arsenale di scienza dei dati.

In questo articolo, abbiamo viaggiato dalle origini del metodo Monte Carlo, attraverso le sue basi teoriche, fino alle sue applicazioni pratiche nell’apprendimento automatico. Abbiamo visto come può essere utilizzato per ottimizzare modelli di apprendimento automatico, con una esplorazione pratica dell’ottimizzazione degli iperparametri utilizzando un set di dati del mondo reale. Abbiamo anche confrontato questo metodo con altri, dimostrandone l’efficienza e l’efficacia.

Ma la storia di Monte Carlo è ancora lungi dall’essere finita. Mentre continuiamo a spingere i limiti dell’apprendimento automatico e della scienza dei dati, il metodo Monte Carlo continuerà senza dubbio a svolgere un ruolo cruciale. Che stiamo sviluppando applicazioni AI sofisticate, dando un senso a dati complessi o semplicemente giocando a un gioco di solitario, il metodo Monte Carlo è una testimonianza del potere della simulazione e dell’approssimazione nella risoluzione di problemi complessi.

Mentre andiamo avanti, prendiamoci un momento per apprezzare la bellezza di questo metodo – un metodo che ha le sue radici in un semplice gioco di carte, ma che ha il potere di guidare alcuni dei calcoli più avanzati al mondo. Il metodo Monte Carlo è veramente un gioco ad alto rischio di casualità e complessità, e finora, sembra che la casa vinca sempre. Quindi, continua a mescolare il mazzo, continua a giocare le tue carte e ricorda – nel gioco della scienza dei dati, il Monte Carlo potrebbe essere proprio il tuo asso nella manica.

Considerazioni finali

Congratulazioni per essere arrivato alla fine! Abbiamo viaggiato nel mondo delle probabilità, lottato con modelli complessi e siamo emersi con una nuova comprensione del potere delle simulazioni Monte Carlo. Li abbiamo visti in azione, semplificando problemi intricati in componenti gestibili e ottimizzando anche gli iperparametri per compiti di apprendimento automatico.

Se ti piace immergerti nelle complessità della risoluzione dei problemi di apprendimento automatico tanto quanto a me, seguimi su VoAGI e LinkedIn. Insieme, affronteremo il labirinto dell’AI, una soluzione intelligente alla volta.

Fino alla nostra prossima avventura statistica, continua ad esplorare, continuare ad imparare e continuare a simulare! E nel tuo percorso di scienza dei dati e apprendimento automatico, che le probabilità siano sempre a tuo favore.

Nota: Tutte le immagini, salvo diversa indicazione, sono dell’autore.