Scoprire il teorema del flusso massimo e del taglio minimo un approccio completo e formale

Teorema del flusso massimo e del taglio minimo un approccio completo e formale.

Esplorare il campo dei network di flusso e il teorema Maxflow Mincut

Introduzione

Nel campo dell’ottimizzazione del flusso di rete, il teorema Maxflow Mincut si distingue come un notevole traguardo matematico. La sua eleganza rappresenta la chiave per risolvere problemi complessi di ottimizzazione riguardanti il flusso di fluidi o risorse attraverso reti composte da nodi interconnessi da archi. Le sue applicazioni includono una vasta gamma di sistemi, dalle reti di trasporto all’infrastruttura delle comunicazioni, dove una gestione efficiente del flusso è essenziale. Comprendendo questo teorema e i concetti fondamentali alla base della sua formulazione matematica, è possibile risolvere i misteri per massimizzare l’utilizzo delle risorse e raggiungere prestazioni ottimali in una varietà di scenari pratici.

In questo articolo, ci proponiamo di semplificare e rendere il teorema accessibile a tutti i lettori. Vi guideremo attraverso lo sviluppo storico, delineando le sue radici dalle prime formulazioni che ci permetteranno di apprezzare i contributi di menti eminenti che hanno aperto la strada a questo teorema e al suo intero ambito di studio matematico. Inoltre, ci immergeremo nelle applicazioni del teorema Maxflow Mincut nel mondo reale. Dalla progettazione di sistemi di trasporto efficienti all’affrontare compiti di elaborazione delle immagini, la sua versatilità sembra illimitata. Esplorando le sue implicazioni pratiche, potrete osservare l’impatto profondo del teorema su campi e settori diversi.

Infine, l’obiettivo è fornirvi una spiegazione completa che coniughi semplicità e formalità. Non è richiesta alcuna competenza precedente in matematica avanzata, anche se una certa conoscenza della teoria dei grafi e della matematica discreta (logica e teoria degli insiemi) può essere di grande aiuto; tutto ciò di cui avete bisogno è una mente curiosa e la volontà di scoprire l’utilità di questo eccezionale teorema.

Storia

Il teorema Maxflow Mincut è stato introdotto per la prima volta da Ford e Fulkerson nel 1956 nel loro lavoro fondamentale “Flusso massimo attraverso una rete”, con la collaborazione di altri matematici rilevanti, come Claude Shannon, responsabile dello sviluppo della teoria dell’informazione. Il teorema afferma che il flusso massimo in una rete è uguale alla capacità minima di un taglio, dove un taglio è una partizione dei nodi della rete in due insiemi disgiunti e la sua capacità è la somma della capacità di tutti gli archi che attraversano il taglio. Da allora, questo teorema è diventato una pietra angolare della teoria dei network di flusso.

• Ingegneria dell’interazione come ingannare l’IA per risolvere i tuoi problemi
• Come ho costruito una pipeline di dati a cascata basata su AWS (Parte 2)
• Organizzare l’AI generativa 5 lezioni apprese dai team di Data Science

Tuttavia, l’introduzione di questo teorema è accompagnata da altre importanti contribuzioni scientifiche come gli algoritmi di Edmonds-Karp, Ford-Fulkerson o Dinic, che tutti servono al compito comune di trovare il flusso massimo che può passare attraverso una rete con sorgente e pozzo. Allo stesso modo, grazie al teorema Maxflow Mincut, questo valore corrisponde al taglio minimo che divide il pozzo dalla sorgente. Inoltre, possiamo utilizzare i calcoli interni degli algoritmi per identificare l’insieme di archi che costituiscono il taglio minimo, come approfondiremo ulteriormente.

Network di flusso

Pertanto, per semplificare la spiegazione del teorema che segue, prima conosceremo i fondamenti e i concetti fondamentali sui network di flusso nella teoria dei grafi.

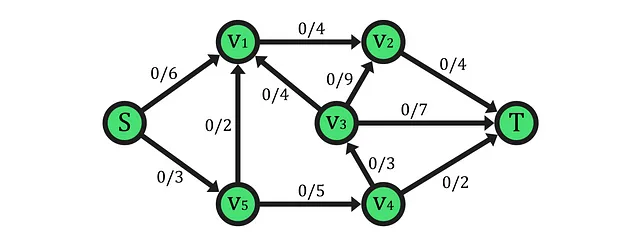
Come si può vedere nell’esempio sopra, un network di flusso è un multigrafo diretto pesato usato per rappresentare un oggetto o un sistema strutturato in rete in cui una certa quantità di risorse, misurate in quello che viene definito “flusso”, deve essere convogliata o spostata da uno o più punti “sorgente” (rappresentati dal nodo S) a uno o più altri nodi chiamati “pozzo” (nodo T). Tuttavia, questo particolare esempio non mostra la proprietà di multigrafo, poiché c’è solo un arco tra due nodi.

Per rappresentare un tale modello, il network di flusso ha pesi associati ad ogni arco. In questo contesto, gli archi pesati modellano una connessione fisica/logica tra diversi punti di scambio di risorse (flusso), dove il valore reale positivo del peso rappresenta la sua capacità (flusso massimo supportato). Sopra, è possibile vedere la capacità rappresentata sul lato destro di ogni etichetta degli archi, così come il flusso corrente che lo attraversa, che in questo caso è 0.

Oltre alla capacità di ogni arco, la metrica cruciale che definisce il tasso a cui le risorse attraversano ogni arco per unità di tempo è il flusso. Puoi pensarlo come il traffico su una strada o la quantità di acqua attraverso un condotto. Pertanto, generato nei nodi sorgente o nel nodo supersorgente se tutte le sorgenti della rete sono collegate a un generatore di flusso principale e portato verso i nodi pozzo o superpozzo se è presente una struttura simile ai pozzi, possiamo definire il flusso come una funzione f:E→R che prende in input un arco (u,v) appartenente all’insieme degli archi del grafo E e restituisce il suo flusso attuale nel tempo f(u,v), che è un valore reale positivo.

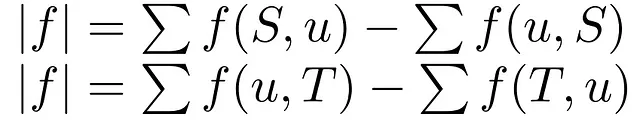
Pertanto, se calcoliamo le espressioni sopra per tutte le sorgenti S o i pozzi T corrispondenti alla rete di flusso, possiamo ottenere la quantità totale di flusso che attraversa il grafo.

Per garantire l’aderenza del flusso ai vincoli della rete, deve soddisfare due proprietà fondamentali:

1. Vincolo di capacità: Il flusso che attraversa un arco non può superare la sua capacità. Formalmente, se la capacità di un arco è indicata come “c(u, v)“, e il flusso attraverso quell’arco è “f(u, v)“, allora deve soddisfare la condizione 0 ≤ f(u, v) ≤ c(u, v) per tutti gli archi (u, v) all’interno della rete. In parole semplici, non possiamo far passare più flusso attraverso un arco di quanto la sua capacità stabilisca.
2. Conservazione del flusso: In ogni nodo (esclusi i nodi sorgente e pozzo), il flusso totale che entra nel nodo deve essere uguale al flusso totale in uscita.

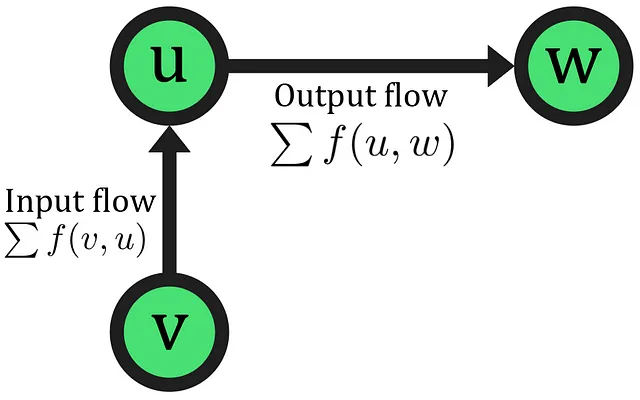
Ciò assicura che il flusso continui senza interruzioni e non si accumuli o si dissipi all’interno della rete, anche se è possibile consentire l’accumulo di flusso se il sistema lo richiede. Matematicamente, per ogni nodo “u” e i suoi nodi vicini rappresentati e raggruppati dai supernodi “v e w“, la proprietà di conservazione del flusso è espressa come:

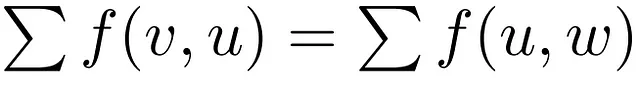
Infine, nota che i flussi possono annullarsi a vicenda, poiché se flussi f1(u,v) e f2(v,u) coesistono tra 2 nodi u e v, quindi diminuire f1(u,v) equivale ad aumentare f2(v,u), poiché hanno direzioni opposte.

Reti residue e percorsi di incremento

Qui introdurremo due concetti nuovi e più sofisticati che saranno di grande aiuto nel trovare flussi massimi utilizzando gli algoritmi precedentemente citati.

Il primo di questi è la differenza tra la capacità di un arco e il suo flusso in un dato momento, chiamata capacità residua e indicata come:

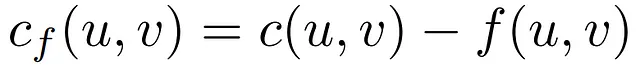
Con questa proprietà in mente, possiamo procedere e definire un particolare tipo di rete di flusso chiamata Rete residua, in cui l’unica differenza con una rete standard è la capacità ridefinita per i suoi archi. Una rete residua conta sulla funzione cf definita sopra che mappa l’insieme degli archi, insieme alle rispettive capacità e flussi, alla capacità residua corrispondente.

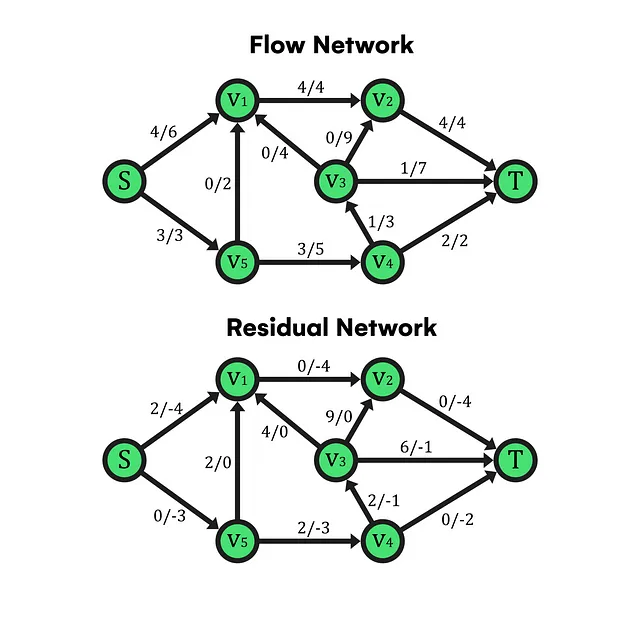
In questo esempio, hai una rete popolata da una specifica funzione di flusso per tutti i suoi archi nel grafico superiore. Di conseguenza, la rete residuale risulta essere quella sottostante, i cui etichette degli archi contengono la capacità residua che può essere inviata secondo la direzione dell’arco corrispondente e la quantità di flusso in direzione opposta che potrebbe essere consegnata in caso di annullamento di un’azione di aumento del flusso (ricorda la proprietà di cancellazione del flusso, che può essere utile in situazioni in cui la rete ha una certa simmetria).

In questo caso, il flusso ottenuto attraverso la rete può essere calcolato con le formule di sorgente o di pozzo come visto in precedenza, che in questo caso sono 7 unità di flusso distribuite in 4+3 unità in uscita da S o, allo stesso modo, 4+1+2 unità in ingresso in T. Tuttavia, se consideriamo l’arco (v5, v1) nella direzione inversa (o bidirezionale), c’è la possibilità di inviare altre 2 unità di flusso lungo il percorso S-V1-V5-V4-V3-T, che aumenterebbe la quantità totale di flusso e diventerebbe la più grande disponibile per la rete data. Successivamente, dopo aver derivato le reti residue, c’è la possibilità che in uno o più percorsi che collegano la sorgente con il pozzo, tutti gli archi abbiano una capacità residua maggiore di 0. In altre parole, ci sono percorsi in cui potremmo trasportare flusso da una sorgente a un pozzo, nel caso in cui ci siano diverse sorgenti o pozzi.

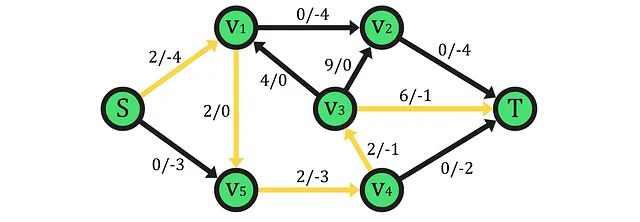
All’interno di questo contesto, tali percorsi sono alla base degli algoritmi utilizzati per risolvere problemi di massimizzazione del flusso o di minimizzazione dei costi e vengono chiamati Percorsi di Aumento. Per capire il motivo, nella rete sopra, possiamo vedere come il flusso stabilito porta all’esistenza di un percorso di aumento attraverso il quale possono essere trasportate 2 unità di flusso da S a T. Di conseguenza, la funzione di flusso effettiva sulla rete non fornisce il flusso massimo trasportabile attraverso di essa, che è uno dei problemi affrontati dal teorema Maxflow Mincut che discuteremo in seguito.

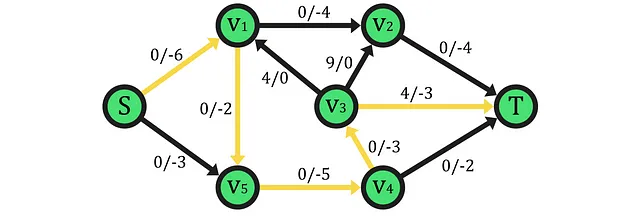
Di conseguenza, se aumentiamo il flusso lungo il percorso mostrato, saremo in grado di garantire che il flusso risultante sia massimale con un valore di 9 unità poiché non ci sarà altro percorso per aumentare il flusso della rete. Infine, prima di introdurre il teorema, è importante tener presente che per trovare il flusso massimo di una rete, gli algoritmi come quello di Ford-Fulkerson utilizzano una procedura intuitiva (greedy) che parte da una rete residuale senza flusso e procede a trovare percorsi di aumento (con l’aiuto di archi residui o flussi in direzione opposta) aumentando il flusso come determinato da questi percorsi. Pertanto, una volta che non ci sono più percorsi da scoprire che aumentano il flusso, si può essere certi che il flusso raggiunto è il massimo, cioè che non c’è un modo più veloce per spostare le risorse da S a T a causa di una mancanza di capacità su alcuni archi o anche di una mancanza di archi nella rete.

Un altro modo per pensare a questa procedura è considerare la quantità di flusso aggiunto per ogni iterazione. Per un percorso di aumento arbitrario, la quantità più elevata che puoi aggiungere è data dall’arco con la capacità residua minore poiché costituisce un collo di bottiglia per il flusso fuori da S. Grazie alla sua capacità di limitare tutto il flusso potenziale lungo un percorso di aumento, un tale Arco Collo di Bottiglia è fondamentale nelle situazioni in cui è necessario massimizzare il flusso.

Ad esempio, considerando la rete di flusso (residuale) semplice superiore con un solo percorso di aumento disponibile, possiamo chiaramente identificare il componente di restringimento del bordo (v2, v3), che determina il flusso massimo dell’intero percorso (e in questo caso della rete) a 3. Dopo aver aumentato il flusso di 3 unità come suggerisce il percorso, non c’è più un percorso di aumento per aumentare ulteriormente il flusso, quindi si conclude che il flusso massimo è stato raggiunto. Tuttavia, un altro modo per garantire la validità del flusso risultante è concentrarsi sui restringimenti all’interno della rete; se ogni percorso tra S e T ha un valore di restringimento nullo, ossia la sua capacità residua massima uguale a 0, che è equivalente all’inesistenza di percorsi di aumento, non è possibile aggiungere altro flusso e quello attuale sarà considerato massimo come visto sopra.

Per risolvere la questione riguardante i restringimenti, dovremmo sottolineare che il flusso massimo può anche essere espresso come la somma di tutti i restringimenti dei percorsi di aumento utilizzati per trovare il flusso massimo tramite algoritmi simili a Ford-Fulkerson, poiché ogni percorso aggiunge flusso quanto determinato dal suo restringimento corrispondente.

Tagli della Rete di Flusso

La parte finale che affronteremo riguardo ai fondamenti delle reti di flusso saranno i Tagli, un componente fondamentale del teorema Maxflow Mincut e un concetto chiave per comprendere le sezioni precedenti, ad esempio il legame tra restringimenti e partizioni di una rete di flusso.

Prima di tutto, iniziamo con la sua definizione; un taglio è una partizione dei nodi della rete in cui il nodo sorgente S è in un insieme A e il pozzo T è in un altro insieme B disgiunto dal precedente.

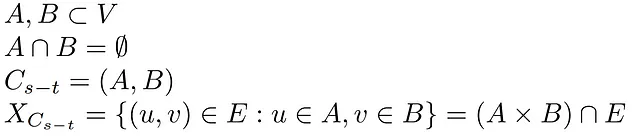
Né l’insieme A né l’insieme B possono essere vuoti, poiché devono contenere rispettivamente le sorgenti e i pozzi. Pertanto, se la rete è connessa, ci saranno bordi che svolgono la funzionalità di connessione tra i nodi di A e B in modo bidirezionale. Inoltre, questi bordi sono contenuti in un altro insieme chiamato insieme di taglio, anche se vengono presi in considerazione solo quelli il cui origine è un nodo in A e termina in B, ossia i bordi in grado di trasportare flusso nella direzione corretta.

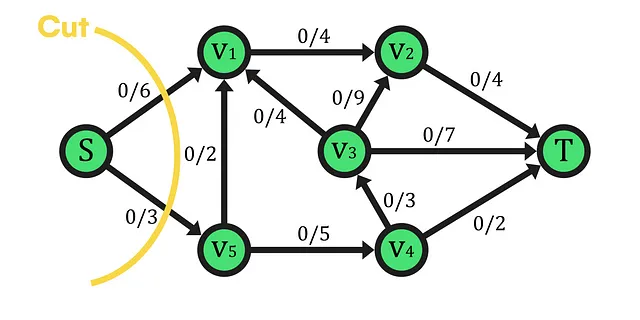
Come esempio, sopra puoi vedere il taglio più semplice che possiamo applicare al grafo, che porta alla partizione dell’insieme dei vertici V come unione degli insiemi A={S} e B={V1,V2,V3,V4,V5,T}. Poiché l’unica sorgente di rete rimane isolata in un insieme, possiamo comprendere più precisamente il concetto di taglio e le sue proprietà successive. Tipicamente, il taglio è rappresentato come una linea che cerca di racchiudere uno dei due insiemi A o B, indistintamente. Inoltre, il confine divisorio attraversa più bordi che fanno parte dell’insieme di taglio, in entrambe le direzioni. Questi bordi sono utilizzati per determinare il flusso e la capacità del taglio, che sono componenti essenziali per stabilire una relazione tra un taglio arbitrario della rete e il flusso. Questo è cruciale per dimostrare il teorema presentato in questo articolo.

Da un lato, il flusso attraverso un taglio dato è definito come la somma di tutti i bordi che trasportano flusso nella direzione A-B, meno il flusso dei bordi che vanno in direzione opposta da B ad A.

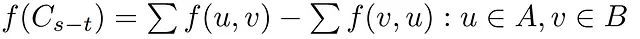
Tuttavia, il flusso non offre un valore significativo in questo contesto, poiché è limitato dalla capacità del taglio. Per questo motivo, possiamo anche definire la capacità di un taglio in modo simile al flusso, con la differenza che qui viene preso in considerazione solo il primo termine della formula sopra, ossia la capacità dei bordi in grado di trasportare il flusso da S a T, senza dover sottrarre nessun altro valore di bordo.

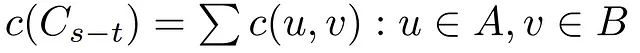
Una volta che abbiamo presentato formalmente il concetto di flusso e capacità nei tagli, diventa necessario considerare alcuni esempi per semplificare queste idee il più possibile e comprendere la loro logica in questo ambito.

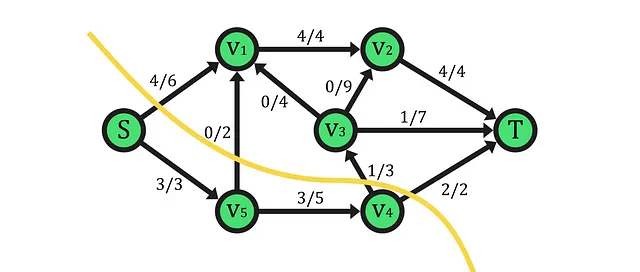
Prima di tutto, esaminiamo i vertici di ciascun insieme, lasciando A={S,V5,V4} e B={V1,V2,V3,T}. Poiché alla rete è già stato assegnato un flusso, il flusso di taglio non sarà zero e sarà determinato dalla somma dei flussi sugli archi che collegano l’insieme A all’insieme B.

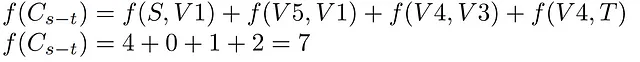
Inoltre, la sua capacità viene ottenuta dagli stessi archi precedenti e dalle rispettive capacità, costituendo il flusso massimo che può attraversare il taglio.

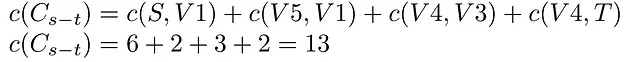
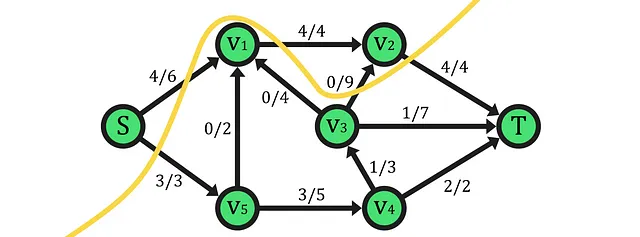
In questo interessante ultimo esempio di taglio, possiamo osservare come un taglio non debba essere una divisione in cui i vertici di entrambi gli insiemi costituiscono componenti connesse, ovvero, ciascun insieme può contenere qualsiasi nodo purché vengano rispettati i vincoli base di un taglio.

Inoltre, questo esempio è particolarmente utile per comprendere la relazione tra i tagli e il flusso, fornendo una solida base prima di affrontare il teorema. Innanzitutto, bisogna tenere presente che secondo la definizione di taglio, la rete risultante (dopo il taglio) è disconnessa rispetto a s-t. Ciò significa che la capacità di tale taglio viene calcolata come la somma di tutti gli archi che vanno dall’assemblea di origine al pozzo. Nel caso più semplice di isolamento della singola sorgente di flusso, la capacità del taglio supererà o sarà uguale al flusso massimo della rete. Tuttavia, negli esempi precedenti, si può apprezzare che inserendo più nodi con archi uscenti, la capacità del taglio aumenta inevitabilmente poiché ci sono più archi di quelli strettamente necessari per raggiungere il flusso massimo, ovvero, gli archi della sorgente sono quelli che determinano, nel caso di restringimenti, il flusso che successivamente attraverserà la rete.

Enunciato del teorema

Il nostro obiettivo principale nel affrontare una sfida di ottimizzazione di una rete di flusso è determinare il flusso massimo raggiungibile che può essere trasmesso dalla sorgente al pozzo. Ciò deve essere realizzato rispettando i limiti di capacità, la conservazione del flusso e garantendo che il flusso ottenuto sia effettivamente massimo. Quindi, il passo che intraprenderemo per affrontare il teorema sarà quello di vincolare tale valore con un limite superiore che può essere calcolato approssimativamente in modo simile al flusso e confermare così la sua correttezza.

Inizialmente, va sottolineato che tale limite superiore si rivela essere un taglio, che soddisfa la proprietà di essere quello con la capacità minore. Come lemma principale del teorema, potrebbe non essere del tutto chiaro, quindi introduciamo e dimostriamo due idee più semplici;

Il primo coinvolge la dimostrazione dell’uguaglianza sopra tra il flusso attraverso qualsiasi taglio dato e il flusso totale di rete, che a sua volta corrisponde al flusso generato dalla sorgente. A questo scopo, possiamo assumere la proposizione iniziale come vera mentre applichiamo il metodo di induzione all’insieme A di qualsiasi taglio, con A = {S} come caso base, e quindi utilizzare il principio precedentemente menzionato della conservazione del flusso per i nodi diversi da S o T. Ma poiché ciò sarebbe complesso da elaborare, opteremo per un approccio più semplice, sebbene molto simile.

Nota che il valore di flusso precedente lungo la dimostrazione può avere qualsiasi valore consentito.

1- Definizione del Flusso: Nel passaggio iniziale, partiamo con il valore di flusso totale per qualsiasi funzione di flusso f in una rete e una delle sue possibili definizioni. Qui, avendo come riferimento il nodo di origine S, che è l’insieme A più piccolo possibile per qualsiasi taglio di rete, facciamo corrispondere il valore del flusso al flusso generato da S meno il flusso in entrata in S poiché a volte potrebbe esserci una certa quantità di flusso che ritorna a S.

2- Proprietà di Conservazione del Flusso: Dopo aver considerato il flusso di rete come il flusso totale generato dalla sorgente S, applichiamo il principio di conservazione del flusso secondo il quale tutti i nodi tranne s-t devono propagare tutto il flusso che ricevono, risultando in un flusso zero contribuito a |f| sottraendo il flusso in uscita meno il flusso in ingresso. Ora, se prendiamo qualsiasi taglio (A,B), il flusso totale contribuito dai nodi v all’interno dell’insieme A eccetto quello che genera il flusso {S} sarà zero, soddisfacendo l’uguaglianza che avevamo prima.

3- Flusso Attraverso un Taglio: Infine, arriviamo a un’espressione in cui sommiamo tutto il flusso in uscita dai nodi di A eccetto S nel secondo termine e il flusso in uscita proprio di S nel primo termine, sottraendo la parte in entrata corrispondente da tutti i nodi precedenti. Ciò corrisponde alla precedente definizione di flusso di taglio e quindi possiamo concludere come conseguenza che tutto il flusso esistente attraverso una rete corrisponderà necessariamente al flusso attraverso qualsiasi taglio dato.

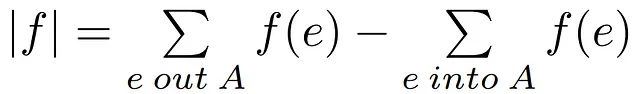
La seconda proposizione che dimostreremo riguardo al teorema di Maxflow Mincut comprende una disuguaglianza che limita superiormente il valore di qualsiasi flusso in una rete con il valore di capacità di qualsiasi taglio dato.

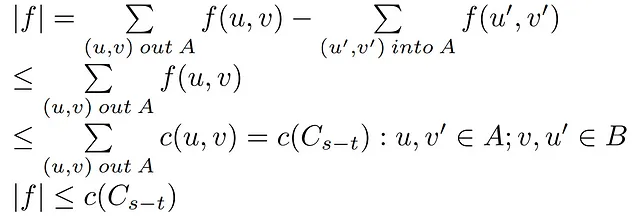
1- Definizione Alternativa del Flusso: Utilizzando il risultato precedente riguardante il flusso di qualsiasi taglio, possiamo rendere uguale un flusso arbitrario |f| al flusso attraverso un taglio arbitrario (A,B).

2/3- Limitazione del Flusso: Nel secondo passaggio, stabiliamo una disuguaglianza che dispensa il secondo termine che modella il flusso in entrata nell’insieme A, lasciando solo il flusso in uscita degli archi che trasportano flusso da A a B. Dopo aver rimosso tale termine, il risultato sarà sempre maggiore o uguale al precedente poiché se non c’è un arco che restituisce flusso da B ad A, la somma dei flussi rimanenti degli archi da A a B non diminuirà.

Quindi, possiamo semplicemente aumentare il valore della disuguaglianza impostando il flusso degli archi in uscita da A come minore o uguale alla capacità di quegli archi. La validità di questa disuguaglianza è data dal vincolo di capacità che appare su tutti gli archi di rete.

4- Dualità Debole: Dopo aver fatto corrispondere la somma di capacità di tutti gli archi in uscita dell’insieme A alla capacità del taglio a causa della sua definizione, si può concludere che per qualsiasi flusso e taglio dati in una rete, il flusso sarà sempre più piccolo o uguale alla capacità del taglio, che si rivela essere il punto di partenza del teorema che stiamo per dimostrare. Inoltre, se cerchiamo di massimizzare il flusso, raggiungeremo un punto che può essere soddisfatto minimizzando la capacità di un taglio, stabilendo una relazione debolmente duale in cui non c’è certezza che un taglio di capacità minima uguale a un flusso massimo esisterà sempre.

A questo punto, dopo aver raggiunto la debolezza della dualità prima del teorema di maxflow mincut, possiamo enunciare una affermazione più facile da comprendere e verificare.

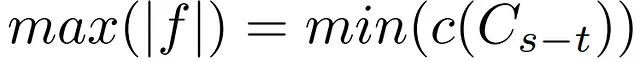
Come già accennato, il teorema si basa sulla Strong Duality che il flusso massimo in qualsiasi rete corrisponde al taglio di capacità minima ottenibile. A differenza del risultato debole della dualità precedente, questo teorema assicura che la massimizzazione del flusso duale è esattamente uguale alla minimizzazione della capacità di qualsiasi taglio, eliminando la possibilità di avere una differenza tra i due risultati e garantendo una condizione di dualità forte sul lemma.

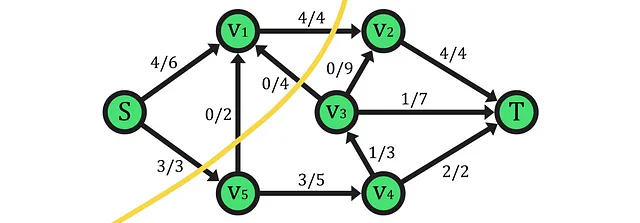
Prima di procedere con la dimostrazione, dovremmo evidenziare un caso d’uso per il teorema. Qui, il flusso massimo ha un valore di 7, che corrisponde alla somma delle capacità di ogni arco di taglio in uscita. Notare che questi archi trasportano il flusso alla loro capacità massima, il che, in un taglio di capacità minima come quello mostrato, fa sì che questi archi siano strozzature, cioè il taglio stesso agisce come una strozzatura del flusso globale di rete. Per condensare l’idea di questa spiegazione, troverai di seguito una risorsa che ti aiuterà a comprenderla:

Qual è una spiegazione intuitiva del teorema di max-flow min-cut?

Sto per leggere la dimostrazione del teorema di max-flow min-cut che aiuta a risolvere il problema del flusso di rete massimo. Potrebbe…

math.stackexchange.com

Dimostrazione

Se vogliamo dimostrare che il flusso di rete massimo è uguale, in tutti i casi, alla capacità minima di taglio in una rete, useremo 3 proposizioni che devono essere equivalenti affinché il teorema sia vero.

Esiste un taglio (A, B) che soddisfa |f|= cap(A, B).

Il valore del flusso |f| è massimo.

Non esiste un percorso di aumento nella rete di flusso.

Per mostrare che tutte le affermazioni sono equivalenti, dimostreremo le implicazioni logiche 1⇒2⇒3⇒1. Ciò significa che possiamo inferire qualsiasi affermazione da un’altra affermazione. Nel caso di 1⇒2, può essere facilmente verificato utilizzando la dualità debole mostrata in precedenza. Quindi, considerando che qualsiasi flusso è più piccolo del taglio con la capacità minore, se assumiamo che esista un flusso uguale alla capacità di un taglio arbitrario (1), la dualità debole ci dice che questa capacità è il limite superiore per qualsiasi flusso dato e quindi il flusso risultante, coincidente con quel limite, è massimale (2).

Procedendo con 2⇒3, il modo più semplice per verificarlo è prendere la contronominale ¬3⇒¬2. Quindi, è sufficiente prendere un flusso arbitrario |f| come esempio, nel caso in cui ci fosse un percorso di aumento s-t ¬(3) che potesse trasportare flusso, |f| potrebbe essere aumentato lungo il percorso corrispondente, il che implica che |f| non era originariamente il flusso massimo ¬(2).

Infine, il passaggio più impegnativo in questa dimostrazione è 3⇒1. Innanzitutto, partiamo assumendo un flusso |f| in cui la rete non ha percorsi di aumento. Inoltre, definiamo un insieme A che contiene tutti i vertici raggiungibili da S nella rete residua. Cioè, A contiene tutti i vertici a cui esiste un percorso da S nella rete residua e allo stesso tempo tutti gli archi residui di quel percorso sono diversi da zero. Attraverso queste definizioni, possiamo essere certi che S sia in A poiché è raggiungibile da solo e poiché non ci sono percorsi di aumento, T non è raggiungibile nella rete residua da S, quindi sappiamo che almeno un nodo (T) non è nell’insieme A. Quindi, se inseriamo T in un insieme diverso B, abbiamo che la coppia (A, B) soddisfa tutti i criteri per essere un taglio valido nella rete.

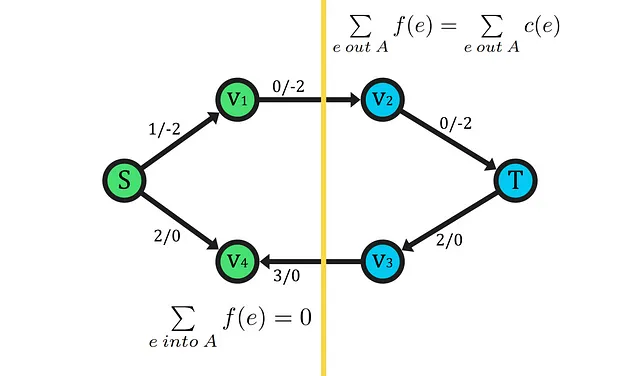
A questo punto, dobbiamo realizzare due cose sul taglio (A, B). Da un lato, il flusso attraverso il taglio nella direzione S-T deve essere uguale alla sua capacità. Perché, dalle definizioni e supposizioni precedenti (3), l’unica possibilità che non fossero uguali risiede nell’accessibilità dei nodi di B, quindi se uno di essi fosse raggiungibile da S nella rete residua, causando il flusso sul lato del taglio di non raggiungere la sua piena capacità, il nodo dovrebbe essere all’interno di A invece che in B, il che è una contraddizione. D’altra parte, il flusso nell’altra direzione del taglio risulta essere zero per la stessa ragione di prima, ovvero se non fosse zero, ci sarebbe un lato nella rete residua nella direzione A-B (flusso del lato residuo rappresentato con segno negativo) che raggiungerebbe il nodo in B e causerebbe la contraddizione.

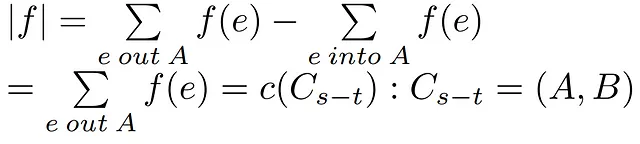
Infine, l’unico compito rimasto da fare è abbinare il flusso di rete al flusso di taglio, che è stato dimostrato in precedenza, rimuovere il termine del flusso nel taglio poiché è nullo, e utilizzare la definizione della capacità del taglio per concludere che il flusso |f| è uguale alla capacità risultante del taglio (3⇒1).

Applicazioni

Il teorema del flusso massimo di taglio ha numerose applicazioni in vari campi. Tuttavia, per renderlo breve, menzioneremo semplicemente alcuni aspetti essenziali dei casi d’uso, insieme a risorse più dettagliate per aiutarti a comprenderli correttamente.

Algoritmi Ford-Fulkerson/Edmonds-Karp

Come prima conseguenza, le scoperte e i risultati forniti dal teorema, in combinazione con altri come il teorema di integralità, portano e supportano la dimostrazione di correttezza di una serie di algoritmi orientati al calcolo del flusso massimo.

Il più significativo di questi, e di cui abbiamo già parlato, è l’algoritmo di Ford-Fulkerson, un approccio greedy che aumenta il flusso cercando percorsi di aumento da s a t. Tuttavia, la versione più basilare dell’algoritmo non ha la garanzia di terminare o convergere al flusso massimo in determinate situazioni con input molto specifici (come lavorare con numeri reali o irrazionali e la loro rappresentazione) a causa del modo in cui sceglie i percorsi di aumento. Ciò influisce anche sulla complessità temporale, che è O(|E| |f|), il che significa che nel caso peggiore, l’algoritmo deve attraversare tutti i lati della rete per ogni (almeno una) unità di flusso contenuta nel massimo da raggiungere.

Quindi, con l’obiettivo di migliorare la versione precedente, che è stata la prima creata per risolvere problemi di questo tipo, il modo di calcolare i percorsi di aumento è stato migliorato. In modo tale che, mentre la versione Ford-Fulkerson utilizzava la ricerca in profondità (DFS), che calcola percorsi casuali per T, la variante migliorata Edmonds-Karp è implementata utilizzando l’algoritmo di ricerca in ampiezza (BFS) per trovare percorsi di aumento. Quindi, con l’obiettivo di scegliere ad ogni iterazione il percorso di aumento con il minor numero possibile di lati, l’algoritmo ha una garanzia di terminazione rispetto a quello precedente, oltre a un cambiamento nella complessità temporale nell’ordine di O(V E²).

Tuttavia, con questi e simili algoritmi, è possibile calcolare non solo il flusso massimo in una rete, ma anche il taglio minimo la cui capacità è uguale al suo valore. La procedura è piuttosto semplice; dopo aver calcolato il flusso massimo in tutti i lati di una rete, secondo il teorema del flusso massimo di taglio, i nodi accessibili da S nella rete residua rimanente costituiscono l’insieme A del taglio che stiamo cercando, mentre i nodi rimanenti costituiscono B e portano al taglio minimo risultante con capacità (A, B).

Infine, va notato che il campo di studio degli algoritmi di flusso massimo è molto più ampio di quanto mostrato qui. Pertanto, se desideri continuare ad apprendere, qui hai una risorsa che tratta questi algoritmi, nonché le loro implementazioni, in modo più dettagliato.

Casi d’uso pratici

Quasi tutti i sistemi con cui interagiamo nella nostra vita hanno il potenziale per essere modellati (almeno in parte) da reti di flusso, che li trasformano in uno strumento cruciale per affrontare problemi complessi di scalabilità. Allo stesso modo, poiché le possibilità sono ampie, qui verranno menzionati solo alcuni casi d’uso che hanno una relazione diretta con i concetti fondamentali.

Innanzitutto, tutti i sistemi di trasporto, dalle reti stradali e i sistemi di trasporto pubblico fino al routing aereo e alla distribuzione delle merci, possono essere rappresentati come reti di flusso. Di conseguenza, possiamo analizzare i modelli di traffico, ottimizzare le rotte e migliorare l’efficienza complessiva. Questo è particolarmente cruciale nella pianificazione urbana, dove gestire il flusso di persone, veicoli e merci è essenziale per prevenire la congestione e garantire un’operatività fluida. Inoltre, non tutti questi casi d’uso sono completamente benefici; ad esempio, le reti di flusso possono anche modellare il sistema ferroviario di un paese, che potrebbe essere preso di mira, in caso di conflitto militare, per attacchi che dovrebbero essere il più strategici possibile. Puoi approfondire ulteriormente questa specifica applicazione in questa risorsa.

Nonostante altre implementazioni trascendentali nelle telecomunicazioni, nella distribuzione di energia o persino nell’assistenza sanitaria, ci concentreremo su una più strettamente associata alle scienze informatiche, in particolare al campo della visione artificiale, che ha ottenuto progressi significativi. Nel campo dell’elaborazione delle immagini, il principale impiego delle reti di flusso si basa sugli algoritmi di segmentazione delle immagini, responsabili di dividere un’immagine in segmenti o regioni che corrispondono a oggetti, soggetti o aree distinte necessarie da individuare, che forse non possono essere distinte dall’occhio umano. In questo contesto, le reti di flusso mettono in mostra la loro abilità modellando le relazioni tra i pixel come una rete, in cui gli archi rappresentano il flusso di valori di probabilità per la similarità/dissimilarità tra pixel adiacenti. Inoltre, vale anche la pena menzionare le applicazioni in ambiti comparabili, come modelli di apprendimento automatico, in cui il concetto di flusso viene utilizzato per ottimizzare specifici compiti di apprendimento, generativi o di classificazione.

Conclusioni

Questo articolo ha coperto solo una piccola parte del dominio matematico delle reti di flusso, dimostrando e semplificando uno dei suoi teoremi fondamentali. Tuttavia, poiché si tratta di un argomento con un vasto numero di applicazioni, in particolare nel sistema di consumo, trasporto e gestione della popolazione mondiale, è utile continuare ad ampliare la teoria e approfondire la conoscenza su queste applicazioni. A tal fine, le risorse più efficaci per osservare formulazioni più avanzate del teorema, nonché per comprendere passo dopo passo gli algoritmi menzionati in questo articolo e apprendere nuovi concetti su determinate applicazioni delle reti di flusso, sono le seguenti:

https://www.cs.upc.edu/~mjserna/docencia/grauA/P20/MaxFlow-fib.pdf

https://ocw.tudelft.nl/wp-content/uploads/Algoritmiek_Introduction_to_Network_Flow.pdf