Operazioni di matrice e vettore nella regressione logistica

'Operazioni matriciali e vettoriali nella regressione logistica'

Regressione Logistica Vettorizzata

La matematica sottostante a qualsiasi algoritmo di Rete Neurale Artificiale (ANN) può essere travolgente da capire. Inoltre, le operazioni di matrice e vettore utilizzate per rappresentare le computazioni di feed-forward e back-propagation durante l’addestramento batch del modello possono contribuire al sovraccarico di comprensione. Mentre le notazioni di matrice e vettore concisi hanno senso, sviscerare tali notazioni fino ai dettagli di funzionamento sottili di tali operazioni di matrice porterebbe maggiore chiarezza. Mi sono reso conto che il modo migliore per capire tali dettagli sottili è considerare un modello di rete minimo. Non ho trovato un algoritmo migliore della Regressione Logistica per esplorare ciò che avviene sotto il cofano perché ha tutti i componenti di un ANN, come input multidimensionali, i pesi della rete, il bias, le operazioni di propagazione in avanti, attivazioni che applicano una funzione non lineare, funzione di perdita e back-propagation basato sui gradienti. Il mio intento per questo blog è condividere le mie note e scoperte sulle operazioni di matrice e vettore che sono fondamentali per il modello di Regressione Logistica.

Breve Sinossi della Regressione Logistica

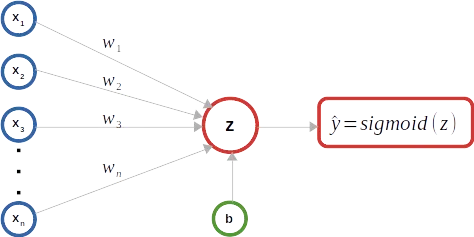
Nonostante il suo nome, la Regressione Logistica è un algoritmo di classificazione e non un algoritmo di regressione. Tipicamente viene utilizzato per la classificazione binaria per prevedere la probabilità che un’istanza appartenga a una delle due classi, ad esempio, prevedere se una email è spam o meno. Pertanto, nella Regressione Logistica, la variabile dipendente o target viene considerata una variabile categorica. Ad esempio, una email che è spam viene rappresentata come 1 e non spam come 0. L’obiettivo principale del modello di Regressione Logistica è stabilire una relazione tra le variabili di input (caratteristiche) e la probabilità della variabile target. Ad esempio, dati le caratteristiche di una email come un insieme di caratteristiche di input, un modello di Regressione Logistica troverebbe una relazione tra tali caratteristiche e la probabilità che la email sia spam. Se ‘Y’ rappresenta la classe di output, come una email che è spam, ‘X’ rappresenta le caratteristiche di input, la probabilità può essere designata come π = Pr( Y = 1 | X, βi), dove βi rappresenta i parametri di regressione logistica che includono i pesi del modello ‘wi’ e un parametro di bias ‘b’. In pratica, una Regressione Logistica prevede la probabilità di Y = 1 dati le caratteristiche di input e i parametri del modello. In modo specifico, la probabilità π è modellata come una funzione logistica a forma di S chiamata funzione Sigmoidale, data da π = e^z/(1 + e^z) o equivalentemente da π = 1/(1 + e^-z), dove z = βi . X. La funzione sigmoidale permette di ottenere una curva liscia compresa tra 0 e 1, rendendola adatta per stimare le probabilità. Fondamentalmente, un modello di Regressione Logistica applica la funzione sigmoidale a una combinazione lineare delle caratteristiche di input per prevedere una probabilità tra 0 e 1. Un approccio comune per determinare la classe di output di un’istanza è la soglia della probabilità prevista. Ad esempio, se la probabilità prevista è maggiore o uguale a 0,5, l’istanza viene classificata come appartenente alla classe 1; altrimenti, viene classificata come classe 0.

Un modello di Regressione Logistica viene addestrato adattando il modello ai dati di addestramento e poi minimizzando una funzione di perdita per regolare i parametri del modello. Una funzione di perdita stima la differenza tra le probabilità previste e quelle effettive della classe di output. La funzione di perdita più comune utilizzata nell’addestramento di un modello di Regressione Logistica è la funzione di Log Loss, anche conosciuta come funzione di Entropia Incrociata Binaria. La formula per la funzione di Log Loss è la seguente:

L = — ( y * ln(p) + (1 — y) * ln(1 — p) )

• DataHour Riduzione delle allucinazioni di ChatGPT dell’80%
• Pic2Word Mappare immagini a parole per il recupero di immagini composte senza training
• I nuovi robot di Amazon stanno portando una rivoluzione dell’automazione.

Dove:

• L rappresenta la Log Loss.
• y è l’etichetta binaria ground-truth (0 o 1).
• p è la probabilità prevista della classe di output.

Un modello di Regressione Logistica regola i suoi parametri minimizzando la funzione di perdita utilizzando tecniche come la discesa del gradiente. Dato un batch di caratteristiche di input e le relative etichette di classe ground-truth, l’addestramento del modello viene effettuato in diverse iterazioni, chiamate epoche. In ogni epoca, il modello esegue operazioni di propagazione in avanti per stimare le perdite e operazioni di propagazione all’indietro per minimizzare la funzione di perdita e regolare i parametri. Tutte queste operazioni in un’epoca utilizzano calcoli di matrici e vettori come illustrato nelle sezioni successive.

Notazioni di Matrici e Vettori

Si prega di notare che ho utilizzato script LaTeX per creare le equazioni matematiche e le rappresentazioni di matrici/vettori incorporate come immagini in questo blog. Se qualcuno fosse interessato agli script LaTeX, non esitate a contattarmi; sarò felice di condividere.

Come mostrato nel diagramma schematico sopra, un classificatore di regressione logistica binaria viene utilizzato come esempio per mantenere le illustrazioni semplici. Come mostrato di seguito, una matrice X rappresenta il numero “m” di istanze di input. Ogni istanza di input comprende un numero “n” di caratteristiche e viene rappresentata come una colonna, un vettore di caratteristiche di input, all’interno della matrice X, rendendola una matrice di dimensioni (n x m). L’esponente superiore (i) rappresenta il numero ordinale del vettore di input nella matrice X. L’indice inferiore ‘j’ rappresenta l’indice ordinale della caratteristica all’interno di un vettore di input. La matrice Y di dimensioni (1 x m) cattura le etichette di verità fondamentale corrispondenti a ciascun vettore di input nella matrice X. I pesi del modello sono rappresentati da un vettore colonna W di dimensioni (n x 1) che comprende “n” parametri di peso corrispondenti a ciascuna caratteristica nel vettore di input. Mentre esiste solo un parametro di bias ‘b’, per illustrare le operazioni di matrice/vettore, viene considerata una matrice B di dimensioni (1 x m) che comprende ‘m’ numero dello stesso parametro di bias b.

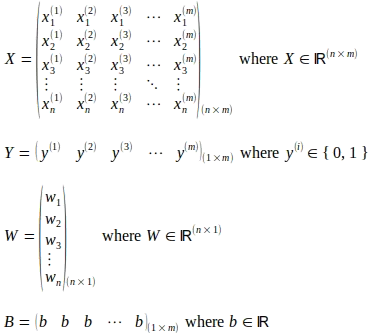
Propagazione in Avanti

Il primo passaggio dell’operazione di propagazione in avanti consiste nel calcolare una combinazione lineare dei parametri del modello e delle caratteristiche di input. La notazione per tale operazione di matrice è mostrata di seguito, dove viene valutata una nuova matrice Z:

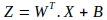
Si noti l’uso della trasposta della matrice dei pesi W. L’operazione sopra nella rappresentazione espansa della matrice è la seguente:

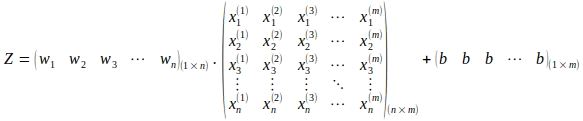
L’operazione di matrice sopra porta al calcolo della matrice Z di dimensioni (1 x m) come mostrato di seguito:

Il passaggio successivo consiste nel derivare le attivazioni applicando la funzione sigmoide alle combinazioni lineari calcolate per ciascun input, come mostrato nell’operazione di matrice seguente. Ciò porta a una matrice di attivazione A di dimensioni (1 x m).

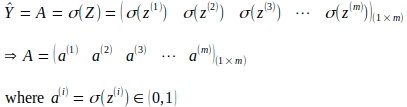
Propagazione all’Indietro

La propagazione all’indietro o back-propagation è una tecnica per calcolare i contributi di ciascun parametro all’errore complessivo o alla perdita causata da previsioni errate alla fine di ogni epoca. I contributi di perdita individuali vengono valutati calcolando i gradienti della funzione di perdita rispetto a (w.r.t) ciascun parametro del modello. Un gradiente o derivata di una funzione è il tasso di variazione o la pendenza di quella funzione rispetto a un parametro considerando gli altri parametri come costanti. Quando viene valutato per un valore o punto specifico del parametro, il segno del gradiente indica in quale direzione la funzione aumenta e l’entità del gradiente indica la ripidezza della pendenza. La funzione di perdita logaritmica come mostrato di seguito è una funzione convessa a forma di ciotola con un unico punto minimo globale. Pertanto, nella maggior parte dei casi, il gradiente della funzione di perdita logaritmica rispetto a un parametro punta nella direzione opposta ai minimi globali. Una volta valutati i gradienti, ciascun valore del parametro viene aggiornato utilizzando il gradiente del parametro, tipicamente utilizzando una tecnica chiamata discesa del gradiente.

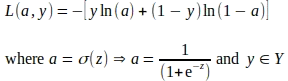
Il gradiente per ciascun parametro viene calcolato utilizzando la regola della catena. La regola della catena consente il calcolo delle derivate di funzioni che sono composte da altre funzioni. Nel caso della regressione logistica, la funzione di perdita logaritmica L è una funzione di attivazione ‘a’ ed etichetta di verità fondamentale ‘y’, mentre ‘a’ stessa è una funzione sigmoide di ‘z’ e ‘z’ è una funzione lineare dei pesi ‘w’ e del bias ‘b’, il che implica che la funzione di perdita L è una funzione composta da altre funzioni come mostrato di seguito.

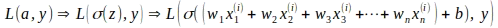
Utilizzando la regola della catena delle derivate parziali, i gradienti dei parametri di peso e bias possono essere calcolati come segue:

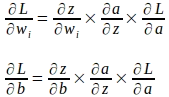
Derivazione dei Gradienti per una Singola Istanza di Input

Prima di esaminare le rappresentazioni matriciali e vettoriali che entrano in gioco come parte dell’aggiornamento dei parametri in un’unica volta, deriviamo prima i gradienti utilizzando una singola istanza di input per comprendere meglio la base di tali rappresentazioni.

Assumendo che ‘a’ e ‘z’ rappresentino i valori calcolati per una singola istanza di input con l’etichetta di verità fondamentale ‘y’, il gradiente della funzione di perdita rispetto a ‘a’ può essere derivato come segue. Si noti che questo gradiente è la prima quantità necessaria per valutare la regola della catena per derivare i gradienti dei parametri successivamente.

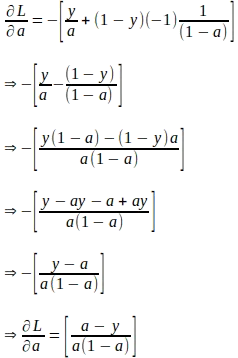
Dato il gradiente della funzione di perdita rispetto a ‘a’, il gradiente della funzione di perdita rispetto a ‘z’ può essere derivato utilizzando la seguente regola della catena:

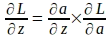
La regola della catena sopra implica che anche il gradiente di ‘a’ rispetto a ‘z’ deve essere derivato. Si noti che ‘a’ viene calcolato applicando la funzione sigmoide a ‘z’. Pertanto, il gradiente di ‘a’ rispetto a ‘z’ può essere derivato utilizzando l’espressione della funzione sigmoide come segue:

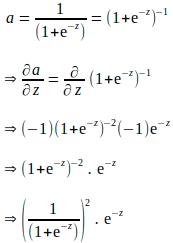
La derivazione sopra è espressa in termini di ‘e’, e sembra che siano necessari ulteriori calcoli per valutare il gradiente di ‘a’ rispetto a ‘z’. Sappiamo che ‘a’ viene calcolato come parte della propagazione in avanti. Pertanto, per eliminare ulteriori calcoli, la derivata sopra può essere completamente espressa in funzione di ‘a’ come segue:

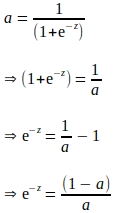
Inserendo i termini sopra espressi in ‘a’, il gradiente di ‘a’ rispetto a ‘z’ è il seguente:

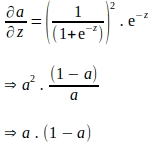
Adesso che abbiamo il gradiente della funzione di perdita rispetto a ‘a’ e il gradiente di ‘a’ rispetto a ‘z’, il gradiente della funzione di perdita rispetto a ‘z’ può essere valutato come segue:

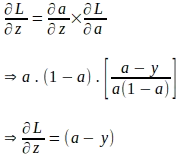
Siamo arrivati ​​lontano nell’elaborazione del gradiente della funzione di perdita rispetto a ‘z’. Dobbiamo ancora valutare i gradienti della funzione di perdita rispetto ai parametri del modello. Sappiamo che ‘z’ è una combinazione lineare dei parametri del modello e delle caratteristiche di un’istanza di input ‘x’ come mostrato di seguito:

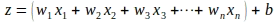
Utilizzando la regola della catena, il gradiente della funzione di perdita rispetto al parametro di peso ‘wi’ viene valutato come mostrato di seguito:

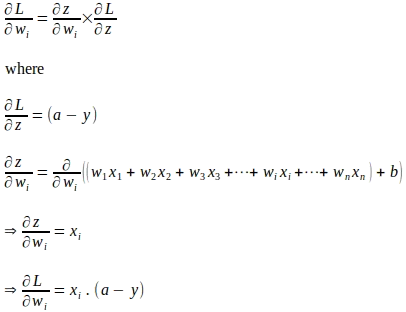
Allo stesso modo, il gradiente della funzione di perdita rispetto a ‘b’ viene valutato come segue:

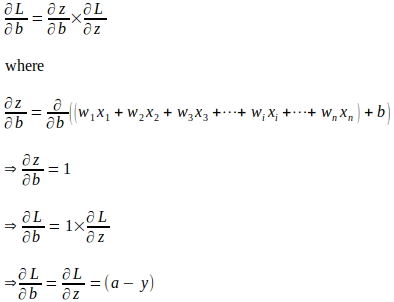
Rappresentazione matriciale e vettoriale degli aggiornamenti dei parametri utilizzando i gradienti

Ora che comprendiamo le formule dei gradienti per i parametri del modello derivati utilizzando una singola istanza di input, possiamo rappresentare le formule in forma matriciale e vettoriale considerando l’intero batch di addestramento. Inizieremo vettorizzando i gradienti della funzione di perdita rispetto a ‘z’ dati dall’espressione seguente:

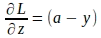
La forma vettoriale di quanto sopra per l’intero numero ‘m’ di istanze è:

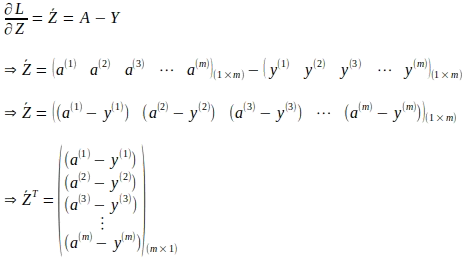
Allo stesso modo, i gradienti della funzione di perdita rispetto ad ogni peso ‘wi’ possono essere vettorizzati. Il gradiente della funzione di perdita rispetto al peso ‘wi’ per una singola istanza è dato da:

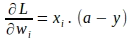
La forma vettoriale di quanto sopra per tutti i pesi in tutte le ‘m’ istanze di input viene calcolata come la media dei gradienti di ‘m’ come segue:

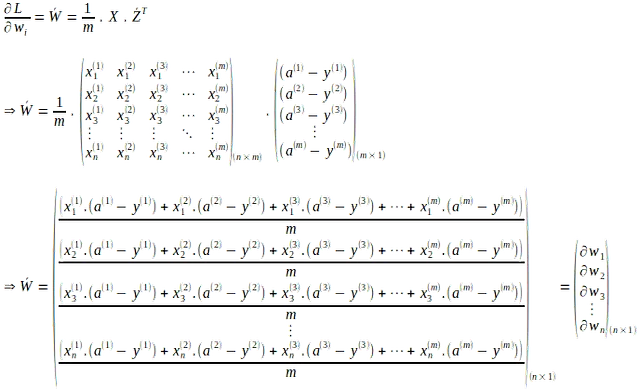
Allo stesso modo, il gradiente risultante della funzione di perdita rispetto a ‘b’ in tutte le ‘m’ istanze di input viene calcolato come la media dei gradienti delle singole istanze come segue:

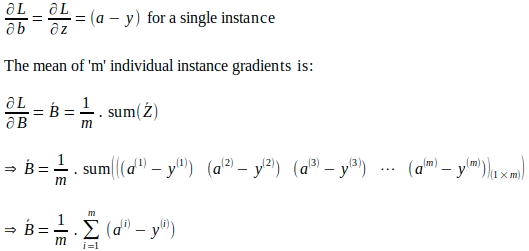
Dato il vettore dei gradienti dei pesi del modello e il gradiente complessivo per il bias, i parametri del modello vengono aggiornati come segue. Gli aggiornamenti dei parametri come mostrato di seguito si basano sulla tecnica chiamata discesa del gradiente, in cui viene utilizzato un tasso di apprendimento. Un tasso di apprendimento è un iperparametro utilizzato nelle tecniche di ottimizzazione come la discesa del gradiente per controllare la dimensione del passo degli aggiustamenti effettuati ad ogni epoca ai parametri del modello in base ai gradienti calcolati. In pratica, un tasso di apprendimento agisce come un fattore di scala che influenza la velocità e la convergenza dell’algoritmo di ottimizzazione.

Conclusioni

Come evidente dalle rappresentazioni matriciali e vettoriali illustrate in questo articolo, la regressione logistica consente a un modello di rete minimo di comprendere i dettagli di funzionamento sottili di tali operazioni matriciali e vettoriali. La maggior parte delle librerie di machine learning racchiude tali dettagli matematici ma invece espone interfacce di programmazione ben definite a un livello superiore, come la propagazione in avanti o all’indietro. Sebbene la comprensione di tutti questi dettagli sottili potrebbe non essere necessaria per sviluppare modelli utilizzando tali librerie, tali dettagli fanno luce sulle intuizioni matematiche dietro tali algoritmi. Tuttavia, tale comprensione sicuramente aiuterà a trasferire le intuizioni matematiche sottostanti ad altri modelli come le reti neurali artificiali (ANN), le reti neurali ricorrenti (RNN), le reti neurali convoluzionali (CNN) e le reti neurali generative avversariali (GAN).