Svelando la Legge dei Grandi Numeri

'Unveiling the Law of Large Numbers' in English.

La LLN è interessante tanto per quello che non dice quanto per quello che dice

Il 24 agosto 1966, un talentuoso drammaturgo di nome Tom Stoppard mise in scena una commedia a Edimburgo, in Scozia. La commedia aveva un titolo curioso, “Rosencrantz e Guildenstern sono morti”. I suoi personaggi principali, Rosencrantz e Guildenstern, sono amici d’infanzia di Amleto (famoso nelle opere di Shakespeare). La commedia si apre con Guildenstern che lancia ripetutamente monete che continuano ad uscire testa. Ogni risultato rende il sacchetto di denaro di Guildenstern più leggero e quello di Rosencrantz più pesante. Mentre il ritmo incessante di teste continua con una spietata persistenza, Guildenstern è preoccupato. Si preoccupa se sta segretamente desiderando che ogni moneta esca testa come una punizione autoinflitta per qualche peccato dimenticato. O se il tempo si è fermato dopo il primo lancio, e lui e Rosencrantz stanno vivendo lo stesso risultato ancora e ancora.

Stoppard fa un lavoro brillante nel mostrare come le leggi della probabilità siano intrecciate nella nostra visione del mondo, nella nostra idea di aspettativa, nel tessuto stesso del pensiero umano. Quando anche il 92° lancio esce testa, Guildenstern chiede se lui e Rosencrantz sono sotto il controllo di una realtà innaturale in cui le leggi della probabilità non operano più.

Le paure di Guildenstern sono ovviamente infondate. Ammesso che la probabilità di ottenere 92 teste di seguito sia inimmaginabilmente piccola. In realtà, è un punto decimale seguito da 28 zeri seguito da 2. Guildenstern ha più probabilità di essere colpito in testa da un meteorite.

Guildenstern deve solo tornare il giorno successivo per lanciare un’altra sequenza di 92 volte la moneta e il risultato sarà quasi certamente molto diverso. Se dovesse seguire questa routine ogni giorno, scoprirà che nella maggior parte dei giorni il numero di teste corrisponderà più o meno al numero di croci. Guildenstern sta vivendo un comportamento affascinante del nostro universo conosciuto come la Legge dei Grandi Numeri.

• Top 15 Software per Big Data da conoscere nel 2023
• Come eseguire la codifica delle etichette in Python?
• PoisonGPT LLM di Hugging Face diffonde notizie false

La Legge dei Grandi Numeri spiegata in modo semplice

La LLN, come viene chiamata, ha due varianti: la debole e la forte. La LLN debole può essere più intuitiva e più facile da comprendere. Ma è anche facile fraintenderla. In questo articolo affronterò la versione debole e lascerò la discussione sulla versione forte per un altro articolo.

La Legge dei Grandi Numeri deboli si occupa della relazione tra la media campionaria e la media della popolazione. Spiegherò cosa dice in modo semplice:

Supponiamo di estrarre un campione casuale di una certa dimensione, diciamo 100, dalla popolazione. A proposito, prendi nota mentale del termine dimensione del campione. La dimensione del campione è il regista, il grande pooh-bah di questa legge. Ora calcola la media di questo campione e mettila da parte. Successivamente, ripeti questo processo molte molte volte. Ciò che otterrai è un insieme di medie imperfette. Le medie sono imperfette perché ci sarà sempre uno “scarto”, una differenza, una deviazione tra esse e la vera media della popolazione. Supponiamo che tu tolleri una certa deviazione. Se selezioni una media campionaria a caso da questo insieme di medie, ci sarà una possibilità che la differenza assoluta tra la media campionaria e la media della popolazione superi la tua tolleranza.

La Legge dei Grandi Numeri deboli afferma che la probabilità che questa deviazione superi il tuo livello di tolleranza si ridurrà a zero man mano che la dimensione del campione aumenta fino all’infinito o fino alla dimensione della popolazione.

Non importa quanto piccolo sia il tuo livello di tolleranza selezionato, man mano che estrai insiemi di campioni di dimensioni sempre maggiori, diventerà sempre meno probabile che la media di un campione scelto a caso dall’insieme superi questa tolleranza.

Un’illustrazione del mondo reale di come funziona la LLN debole

Per vedere come funziona la LLN debole, la metteremo in pratica con un esempio. E per questo, permettetemi, se volete, di portarvi nella fredda e cupa estensione dell’Oceano Atlantico Nordorientale.

Ogni giorno, il Governo dell’Irlanda pubblica un dataset di misurazioni della temperatura dell’acqua prelevate dalla superficie del Nord Est dell’Atlantico settentrionale. Questo dataset contiene centinaia di migliaia di misurazioni della temperatura dell’acqua di superficie indicizzate per latitudine e longitudine. Ad esempio, i dati del 21 giugno 2023 sono i seguenti:

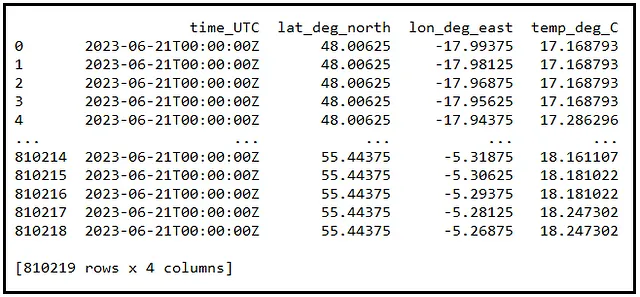
È difficile immaginare come siano fatti ottocentomila valori di temperatura di superficie. Quindi creiamo un grafico a dispersione per visualizzare questi dati. Ho mostrato questo grafico di seguito. Le aree bianche vuote nel grafico rappresentano l’Irlanda e il Regno Unito.

Come studente di statistica, non avrai mai accesso alla “popolazione”. Quindi avrai ragione a criticarmi severamente se dichiaro questa popolazione di 800.000 misurazioni di temperatura come la “popolazione”. Ma sopportami per un po’. Presto vedrai perché, nella nostra ricerca per capire il LLN, ci aiuta considerare questi dati come la “popolazione”.

Quindi supponiamo che questi dati siano – ehm…tosse – la popolazione. La temperatura media dell’acqua di superficie nelle 810.219 posizioni di questa popolazione di valori è di 17,25840 gradi Celsius. 17,25840 è semplicemente la media delle 810K misurazioni di temperatura. Designeremo questo valore come la media della popolazione, μ. Ricorda questo valore. Avrai bisogno di consultarlo spesso.

Ora supponiamo che questa popolazione di 810.219 valori non sia accessibile a te. Invece, hai accesso solo a un piccolo campione di 20 posizioni casuali estratte da questa popolazione. Ecco un tale campione casuale:

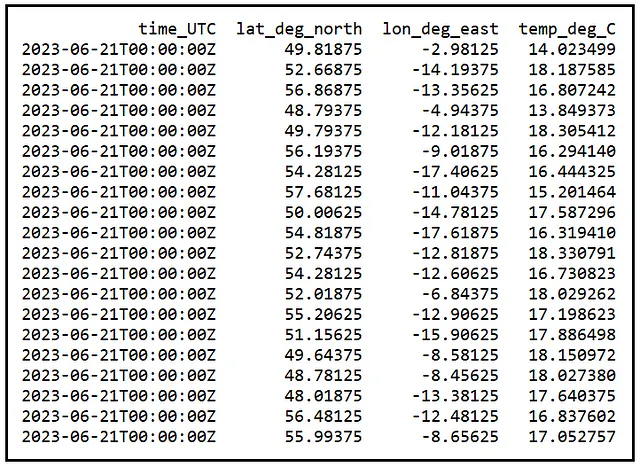
La temperatura media del campione è di 16,9452414 gradi C. Questa è la nostra media del campione X_bar che viene calcolata come segue:

X_bar = (X1 + X2 + X3 + … + X20) / 20

Puoi facilmente estrarre un secondo, un terzo, in effetti qualsiasi numero di tali campioni casuali di dimensione 20 dalla stessa popolazione. Ecco alcuni campioni casuali a titolo illustrativo:

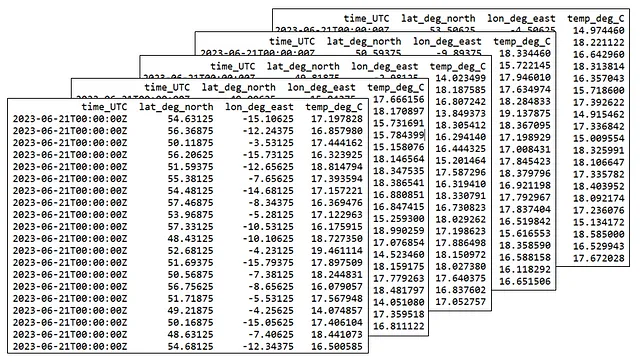
Una breve digressione su cosa sia realmente un campione casuale

Prima di andare avanti, fermiamoci un attimo per ottenere un certo grado di prospettiva sul concetto di campione casuale. Renderà più facile capire come funziona il debole LLN. E per acquisire questa prospettiva, devo presentarti la slot machine del casinò:

La slot machine mostrata sopra contiene tre slot. Ogni volta che abbassi la leva della macchina, la macchina riempie ogni slot con un’immagine selezionata casualmente dalla popolazione di immagini mantenuta internamente come una lista di immagini di frutta. Ora immagina una slot machine con 20 slot chiamati X1 attraverso X20. Supponi che la macchina sia progettata per selezionare valori da una popolazione di 810.219 misurazioni di temperatura. Quando tiri la leva, ognuno dei 20 slot – X1 attraverso X20 – si riempie con un valore selezionato casualmente dalla popolazione di 810.219 valori. Pertanto, X1 attraverso X20 sono variabili casuali che possono contenere qualsiasi valore dalla popolazione. Insieme formano un campione casuale. In altre parole, ogni elemento di un campione casuale è esso stesso una variabile casuale.

X1 attraverso X20 hanno alcune proprietà interessanti:

• Il valore che X1 acquisisce è indipendente dai valori che X2 fino a X20 acquisiscono. Lo stesso si applica a X2, X3, …, X20. Pertanto X1 fino a X20 sono variabili casuali indipendenti.
• Poiché X1, X2, …, X20 possono assumere qualsiasi valore dalla popolazione, la media di ognuno di essi è la media della popolazione, μ. Utilizzando la notazione E() per l’aspettazione, scriviamo questo risultato come segue: E(X1) = E(X2) = … = E(X20) = μ.
• X1 fino a X20 hanno distribuzioni di probabilità identiche.

Pertanto, X1, X2, …, X20 sono variabili casuali indipendenti e identicamente distribuite (i.i.d.).

…e ora torniamo a mostrare come funziona il teorema debole del limite inferiore

Calcoliamo la media (indicata da X_bar) di questo campione di 20 elementi e mettiamola da parte. Ora abbassiamo ancora una volta il braccio della macchina e fuoriuscirà un altro campione casuale di 20 elementi. Calcoleremo la sua media e la metteremo da parte anche questa volta. Se ripetiamo questo processo mille volte, avremo calcolato mille medie campionarie.

Ecco una tabella di 1000 medie campionarie calcolate in questo modo. Le designiamo come X_bar_1 a X_bar_1000:

Ora considera attentamente la seguente affermazione:

Dato che la media campionaria è calcolata da un campione casuale, la media campionaria è essa stessa una variabile casuale.

A questo punto, se stai annuendo saggiamente e ti stai accarezzando il mento, è molto giusto farlo. La consapevolezza che la media campionaria è una variabile casuale è una delle realizzazioni più penetranti che si possono avere in statistica.

Notate anche come ogni media campionaria nella tabella sopra sia a una certa distanza dalla media della popolazione, μ. Tracciamo un istogramma di queste medie campionarie per vedere come sono distribuite intorno a μ:

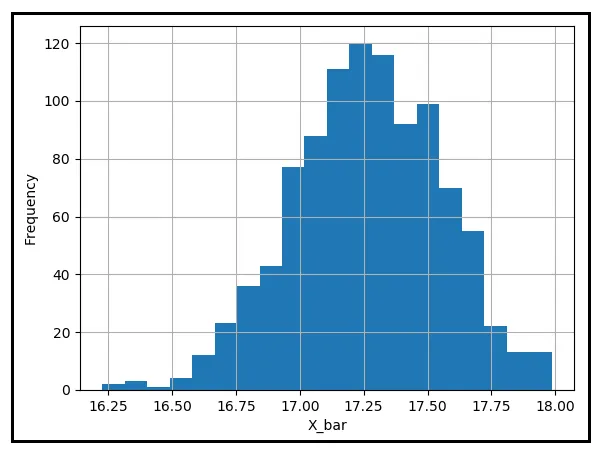
La maggior parte delle medie campionarie sembra essere vicina alla media della popolazione di 17.25840 gradi Celsius. Tuttavia, ce ne sono alcune che sono considerevolmente distanti da μ. Supponiamo che la tua tolleranza per questa distanza sia di 0.25 gradi Celsius. Se immergessi la mano in questo secchio di 1000 medie campionarie, prendessi la media che si trova nel tuo campo di presa e la tirassi fuori. Qual sarà la probabilità che la differenza assoluta tra questa media e μ sia uguale o superiore a 0.25 gradi C? Per stimare questa probabilità, devi contare il numero di medie campionarie che sono almeno a 0.25 gradi di distanza da μ e dividere questo numero per 1000.

Nella tabella sopra, questo conteggio risulta essere 422 e quindi la probabilità P(|X_bar — μ | ≥ 0.25) risulta essere 422/1000 = 0.422

Parcheggiamo questa probabilità per un minuto.

Ora ripeti tutti i passaggi precedenti, ma questa volta utilizza una dimensione del campione di 100 invece di 20. Quindi ecco cosa farai: estrai 1000 campioni casuali ciascuno di dimensione 100, prendi la media di ogni campione, conserva tutte quelle medie, conta quelle che sono almeno a 0.25 gradi C di distanza da μ e dividi questo conteggio per 1000. Se tutto ciò ti è sembrato il lavoro di Ercole, non ti sbagliavi. Quindi prenditi un momento per riprendere fiato. E una volta che sei tutto aggiornato, noterai qui sotto quello che hai ottenuto come frutto dei tuoi sforzi.

La tabella qui di seguito contiene le medie delle 1000 campioni casuali, ognuno delle dimensioni di 100:

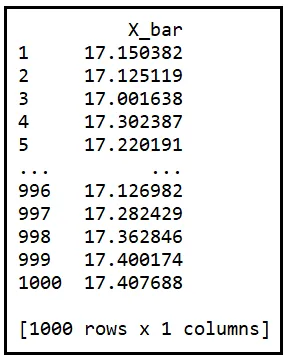
Di queste mille medie, cinquantasei medie si discostano almeno di 0,25 gradi Celsius da μ. Ciò ti dà la probabilità di incontrare una tale media come 56/1000 = 0,056. Questa probabilità è decisamente più piccola rispetto allo 0,422 che abbiamo calcolato in precedenza quando la dimensione del campione era solo 20.

Se ripeti questa sequenza di passi più volte, ogni volta con una diversa dimensione del campione che aumenta incrementando, otterrai una tabella piena di probabilità. Ho fatto questo esercizio per te aumentando la dimensione del campione da 10 a 490 con incrementi di 10. Ecco il risultato:

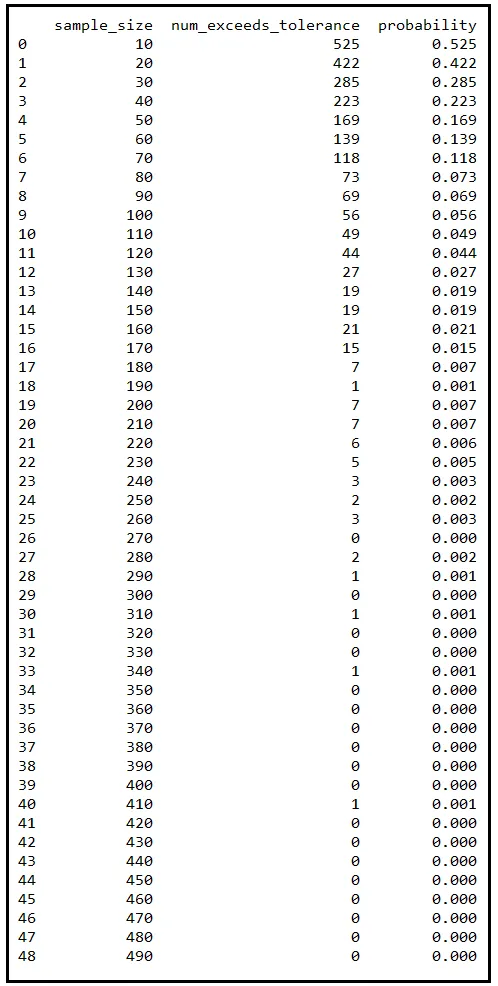
Ogni riga in questa tabella corrisponde a 1000 campioni diversi che ho estratto casualmente dalla popolazione di 810219 misurazioni di temperatura. La colonna sample_size indica la dimensione di ciascuno di questi 1000 campioni. Una volta estratto, ho preso la media di ciascun campione e ho contato quelli che si discostavano almeno di 0,25 gradi Celsius da μ. La colonna num_exceeds_tolerance menziona questo conteggio. La colonna probability è num_exceeds_tolerance / sample_size.

Nota come questo conteggio si attenua rapidamente all’aumentare della dimensione del campione. E così fa anche la corrispondente probabilità P(|X_bar — μ | ≥ 0,25). Quando la dimensione del campione raggiunge 320, la probabilità si è ridotta a zero. Ogni tanto sale a 0,001 ma questo è perché ho estratto un numero finito di campioni. Se ogni volta estraggo 10000 campioni invece di 1000, non solo le occasionali fluttuazioni si appiattiranno ma anche l’attenuazione delle probabilità diventerà più regolare.

Il grafico seguente rappresenta P(|X_bar — μ | ≥ 0,25) in funzione della dimensione del campione. Mette in evidenza come la probabilità scenda a zero all’aumentare della dimensione del campione.

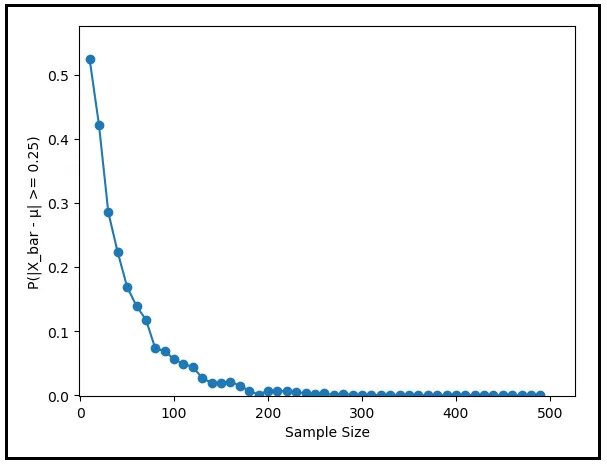
Al posto di 0,25 gradi Celsius, cosa succede se scegli un valore di tolleranza diverso, sia più basso che più alto? La probabilità si abbassa indipendentemente dal livello di tolleranza selezionato? La seguente famiglia di grafici illustra la risposta a questa domanda.

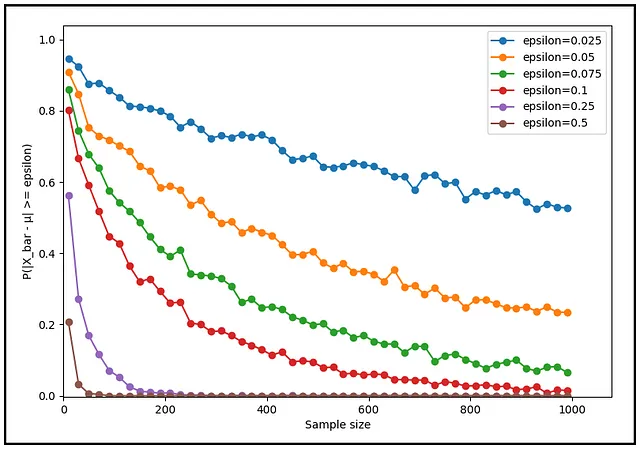
Non importa quanto piccola, quanta piccola sia la tua scelta di tolleranza (ε), la probabilità P(|X_bar — μ | ≥ ε) convergerà sempre a zero all’aumentare della dimensione del campione. Questo è il debole Legge dei Grandi Numeri in azione.

La legge debole dei grandi numeri, enunciata formalmente

Il comportamento della legge debole dei grandi numeri può essere enunciato formalmente come segue:

Sia X1, X2, …, Xn delle variabili casuali indipendenti ed identicamente distribuite che formano insieme un campione casuale di dimensione n. Supponiamo che X_bar_n sia la media di questo campione. Supponiamo inoltre che E(X1) = E(X2) = … = E(Xn) = μ. Allora per ogni numero reale non negativo ε, la probabilità che X_bar_n sia almeno ε lontano da μ tende a zero all’aumentare della dimensione del campione. La seguente esatta equazione cattura questo comportamento:

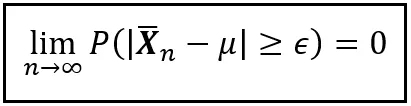
Nel corso dei 310 anni di storia di questa legge, i matematici sono stati in grado di rilassare progressivamente il requisito che X1 attraverso Xn siano indipendenti ed identicamente distribuite pur preservando lo spirito della legge.

Il principio della “convergenza in probabilità”, la notazione “plim” e l’arte di dire cose davvero importanti in poche parole

Lo stile particolare di convergenza verso un certo valore utilizzando la probabilità come mezzo di trasporto è chiamato convergenza in probabilità. In generale, viene enunciato come segue:

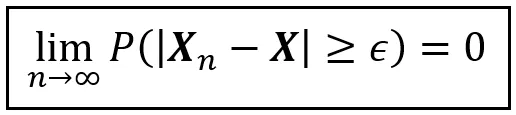
Nell’equazione sopra, X_n e X sono variabili casuali. ε è un numero reale non negativo. L’equazione afferma che al tendere di n all’infinito, X_n converge in probabilità a X.

In tutta l’immensa estensione della statistica, ti imbatterai in una notazione silenziosamente modesta chiamata plim. Si pronuncia ‘p lim’, o ‘plim’ (come la parola ‘prugna’ ma con una ‘i’), o limite di probabilità. plim è il modo abbreviato di dire che una misura come la media converge in probabilità a un valore specifico. Utilizzando plim, la legge debole dei grandi numeri può essere enunciata in modo conciso come segue:

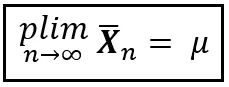
O semplicemente come:

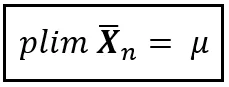
La concisione della notazione non sorprende affatto. I matematici sono attratti dalla concisione come le api dal nettare. Quando si tratta di esprimere verità profonde, la matematica potrebbe essere il campo più efficiente in termini di inchiostro. E all’interno di questo campo ossessionato dall’efficienza, plim occupa una posizione di rilievo. Ti sarà difficile scoprire un concetto altrettanto profondo come plim espresso con una quantità inferiore di inchiostro o elettroni.

Ma non lottare più. Se la bellezza laconica di plim ti ha lasciato desideroso di più, ecco un’altra notazione, forse ancora più efficiente, che trasmette lo stesso significato di plim:

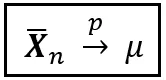
Smentendo alcuni miti sul debole LLN

All’inizio di questo articolo, ho menzionato che il debole teorema dei grandi numeri è degno di nota per ciò che non dice tanto quanto per ciò che dice. Per spiegare cosa intendo con ciò, lasciatemi spiegare. Il debole LLN viene spesso frainteso nel senso che, all’aumentare delle dimensioni del campione, la sua media si avvicina alla media della popolazione o a varie generalizzazioni di tale idea. Come abbiamo visto, tali idee sul debole LLN non hanno alcun attaccamento alla realtà.

Infatti, smentiamo subito un paio di miti riguardanti il debole LLN.

MITO #1: All’aumentare delle dimensioni del campione, la media del campione tende alla media della popolazione.

Questo è probabilmente il fraintendimento più comune del debole LLN. Tuttavia, il debole LLN non fa tale affermazione. Per capire perché, considerate la seguente situazione: siete riusciti ad ottenere un campione molto grande. Mentre ammirate con gioia il vostro successo, dovreste anche porvi le seguenti domande: solo perché il vostro campione è grande, deve anche essere ben bilanciato? Cosa impedisce alla natura di colpirvi con un campione gigante che contiene una quantità altrettanto gigante di distorsione? La risposta è assolutamente nulla! In effetti, non è quello che è successo a Guildenstern con la sua sequenza di 92 teste? Era, dopo tutto, un campione completamente casuale! Se capita di avere una grande distorsione, allora nonostante le grandi dimensioni del campione, la distorsione spazzerà via la media del campione fino ad un punto lontano dal vero valore della popolazione. Al contrario, un piccolo campione può rivelarsi esquisitamente ben bilanciato. Il punto è che, all’aumentare delle dimensioni del campione, la media del campione non è garantita di avanzare obedientemente verso la media della popolazione. La natura non fornisce tali garanzie superflue.

MITO #2: All’aumentare delle dimensioni del campione, praticamente tutto riguardo al campione – la mediana, la varianza, la deviazione standard – converge ai valori della popolazione dello stesso.

Questa frase contiene due miti racchiusi in un pacchetto facile da trasportare. In primo luogo, il debole LLN postula una convergenza in probabilità, non in valore. In secondo luogo, il debole LLN si applica alla convergenza in probabilità solo della media del campione, non di altre statistiche. Il debole LLN non affronta la convergenza di altre misure come la mediana, la varianza o la deviazione standard.

Come sapere se il debole teorema dei grandi numeri funziona?

È una cosa affermare il debole LLN e persino dimostrare come funziona usando dati del mondo reale. Ma come puoi essere sicuro che funzioni sempre? Ci sono circostanze in cui rovinerà il divertimento – situazioni in cui la media del campione semplicemente non converge in probabilità al valore della popolazione? Per saperlo, devi dimostrare il debole LLN e, nel farlo, definire precisamente le condizioni in cui si applicherà.

Casualmente, il debole LLN ha una deliziosa e invitante prova che utilizza come uno dei suoi ingredienti l’infinitamente affascinante Ineguaglianza di Chebyshev. Se questo stimola il tuo appetito, rimani sintonizzato per il mio prossimo articolo sulla prova del debole teorema dei grandi numeri.

Rivedendo Guildenstern

Sarebbe scortese lasciare questo argomento senza lenire le preoccupazioni del nostro amico Guildenstern. Sviluppiamo un’apprezzamento per quanto incredibilmente improbabile sia stato il risultato che ha sperimentato. Simuleremo l’atto di lanciare 92 monete imparziali utilizzando un generatore pseudo-casuale. Teste saranno codificate come 1 e croci come 0. Registriamo il valore medio dei 92 risultati. Il valore medio è la frazione di volte in cui la moneta è uscita testa. Ripeteremo questo esperimento diecimila volte per ottenere diecimila medie di 92 lanci di monete e tracceremo la loro distribuzione di frequenza. Dopo aver completato questo esercizio, otterremo il seguente tipo di istogramma:

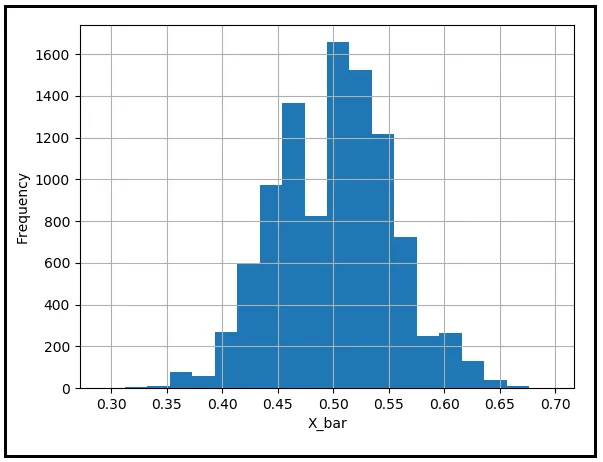
Vediamo che la maggior parte delle medie del campione è raggruppata intorno alla media della popolazione di 0,5. Il risultato di Guildenstern – ottenere 92 teste di fila – è un risultato eccezionalmente improbabile. Pertanto, la frequenza di questo risultato è anche estremamente bassa. Ma contrariamente alle paure di Guildenstern, non c’è nulla di innaturale nel risultato e le leggi della probabilità continuano a operare con il loro solito entusiasmo. Il risultato di Guildenstern si nasconde semplicemente nelle regioni remote della coda sinistra del grafico, in attesa con infinita pazienza di balzare su qualche sfortunato giramonete che ha commesso l’unico errore di essere incredibilmente sfortunato.

Riferimenti e Diritti d’autore

Set di dati

Il set di dati North East Atlantic Real Time Sea Surface Temperature scaricato da DATA.GOV.IE in base a CC BY 4.0

Immagini

Tutte le immagini in questo articolo sono protette da copyright Sachin Date in base a CC-BY-NC-SA, a meno che una fonte e un diritto d’autore diversi non vengano menzionati sotto l’immagine.

Grazie per la lettura! Se ti è piaciuto questo articolo, ti preghiamo di seguirmi per ricevere consigli, guide e consigli di programmazione su regressione e analisi di serie temporali.