Troppe funzionalità? Analizziamo l’Analisi delle Componenti Principali

Too many features? Let's analyze Principal Component Analysis.

Serie di modelli di machine learning fatti in casa

Il repository di supporto è disponibile qui!

La maledizione della dimensionalità è uno dei problemi principali nel machine learning. All’aumentare del numero di features, aumenta anche la complessità del modello. Inoltre, se non ci sono dati sufficienti per l’addestramento, si verifica l’overfitting.

In questo articolo, verrà introdotta l’Analisi delle Componenti Principali (PCA). Inizierò spiegando perché troppe features sono un problema. Poi, spiegherò la matematica dietro la PCA e perché funziona. Inoltre, la PCA verrà suddivisa in passaggi, accompagnati da esempi visivi e frammenti di codice. Inoltre, saranno spiegati i vantaggi e gli svantaggi della PCA. Infine, questi passaggi saranno racchiusi in una classe Python per un uso futuro.

Nota per il lettore: Se non sei interessato alla spiegazione matematica e vuoi solo vedere gli esempi pratici e capire come funziona la PCA, vai alla sezione “PCA in pratica”. Se sei interessato solo alla classe Python, vai a “Implementazione PCA fatta in casa”.

• Padronizzare l’Ingegneria dei Prompt per Sfruttare il Potenziale di ChatGPT
• Oltre i Numeri Il Ruolo Cruciale delle Soft Skills nell’Analisi dei Dati
• Esplorazione delle tendenze e modelli di conflitto Analisi dei dati ACLED di Manipur

Qual è il problema con troppe features?

Diamo un’occhiata allo spazio delle features nella Figura 1. Ci sono pochi esempi per riempire tutto lo spazio, quindi un modello di questi dati potrebbe non generalizzare bene su nuovi esempi non visti.

Cosa succede se aggiungiamo un’altra feature? Diamo un’occhiata al nuovo spazio delle features nella Figura 2. Si può vedere che c’è ancora più spazio vuoto rispetto all’esempio precedente. All’aumentare del numero di features, il modello farà l’overfitting sui dati attuali. Ecco perché ci sono tecniche per ridurre la dimensionalità dei dati e alleviare questo problema. [1]

Qual è lo scopo della PCA?

In poche parole, lo scopo della PCA è estrarre nuove features non correlate di dimensioni inferiori che massimizzano la quantità di informazioni mantenute dai dati originali. La misura delle informazioni in questo contesto è la varianza. Vediamo perché:

Questa tecnica si basa sull’assunzione che il nostro punto dati d-dimensionale x possa essere rappresentato da una combinazione lineare di vettori di una base ortonormale [1]:

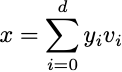
Non preoccuparti, spiegherò da dove vengono i vettori di questa base in seguito. Inoltre, possiamo estrarre una rappresentazione x̂ usando m dei d vettori nella combinazione (m < d):

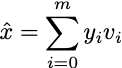
Certo, non otteniamo una rappresentazione esatta poiché ci sono meno caratteristiche, ma almeno cerchiamo di minimizzare la perdita di informazioni. Definiamo l’Errore quadratico medio (MSE) tra l’esempio originale x e l’approssimazione x̂:

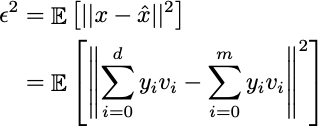
Poiché le sommatorie utilizzano le stesse variabili con tagli diversi, la differenza è solo l’offset:

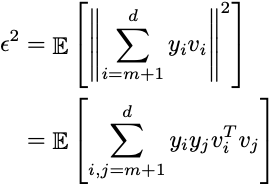
Sappiamo, dalla nostra ipotesi iniziale, che x è la somma di vettori ortonormali. Quindi, il prodotto scalare di questi vettori è zero e ciascuna delle loro norme euclidee è uno. Pertanto:

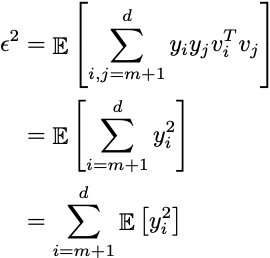
Risolvendo il valore di importanza yi:

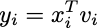
Inserendo tale risultato nella sua aspettativa:

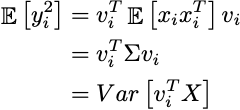
Possiamo vedere che se xi è centrato (media uguale a zero), allora l’aspettativa risulta essere la matrice di covarianza di tutti i dati, e questo risultato non è altro che la varianza nello spazio originale. Scegliendo i giusti vettori vi che massimizzano la varianza, minimizzeremo efficacemente l’errore di rappresentazione.

Da dove proviene questa base ortonormale?

Come già detto, vogliamo ottenere m vettori che massimizzino la varianza:

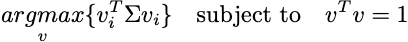
Se prendiamo l’intera matrice dei dati, si può vedere che vi è una direzione di proiezione. I dati verranno proiettati in uno spazio di dimensionalità inferiore.

Se diagonalizziamo la matrice di covarianza Σ utilizzando la decomposizione spettrale otteniamo:

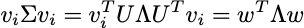
Dove U è una matrice con gli autovettori normalizzati di Σ e Λ è una matrice diagonale che contiene gli autovalori di Σ in ordine decrescente. Ciò è possibile poiché Σ è una matrice reale e simmetrica.

Inoltre, poiché Λ contiene solo valori diversi da zero sulla diagonale, possiamo riscrivere l’equazione precedente come:

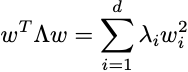
con:

Si noti che i vettori in U e il vettore v sono normalizzati . Pertanto, quando si effettua il prodotto scalare quadrato di ciascun v con a, si ottiene un valore compreso tra [0,1] e quindi w deve essere anch’esso un vettore normalizzato:

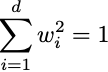
Da qui, emergono proprietà interessanti.

La prima componente principale

Ricordiamo il problema di ottimizzazione. Poiché gli autovalori sono ordinati e w deve essere un vettore normalizzato, la nostra migliore opzione è ottenere il primo autovettore con w = (1,0,0,…). Di conseguenza, il limite superiore viene raggiunto quando:

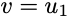
La direzione di proiezione che massimizza la varianza risulta essere l’autovettore associato all’autovalore più grande!

Il resto dei componenti

Una volta impostata la prima componente principale, viene aggiunta una nuova restrizione al problema di ottimizzazione:

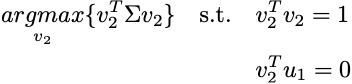
Ciò significa che il nuovo componente v2 deve essere ortogonale al componente precedente, l’autovettore u1, in modo che le informazioni non siano ridondanti. Si può dimostrare che tutti i d componenti corrispondono ai d autovettori normalizzati da Σ associati agli autovalori, in ordine decrescente. Dai un’occhiata a queste note per la dimostrazione formale di questa affermazione [2].

PCA in pratica

Dalla descrizione teorica sopra, si possono descrivere i passaggi necessari per ottenere le componenti principali di un insieme di dati. Il dataset iniziale è un campione casuale della seguente distribuzione normale 2D:

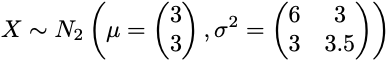
from scipy import statsmean = [3,3]var = [[6, 3],       [3, 3.5]]n = 100data_raw = np.random.multivariate_normal(mean, var, 100)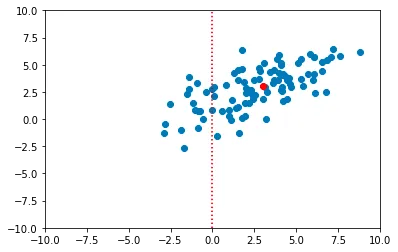

1. Centratura dei dati

Il primo passo è spostare la nuvola all’origine del sistema di coordinate in modo che i dati abbiano media zero. Questo passaggio viene eseguito sottraendo la media campionaria da ogni punto nel dataset.

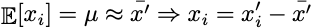
import numpy as npdata_centered = data_raw - np.mean(data_raw, axis=0)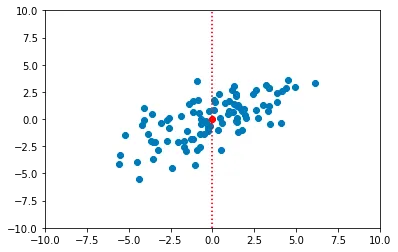

2. Calcolo della matrice di covarianza

La varianza definita sopra è la matrice di covarianza della popolazione Σ. In pratica, quella informazione non è a nostra disposizione poiché abbiamo solo un campione. Pertanto, possiamo approssimare tale parametro utilizzando la covarianza campionaria S.

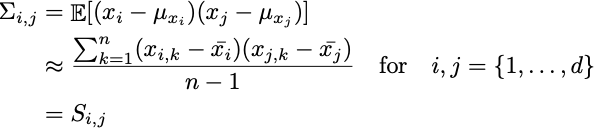
Ricorda che i dati sono già centrati. Quindi:

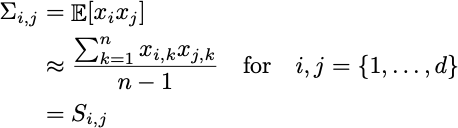
Possiamo scrivere ciò in modo compatto utilizzando moltiplicazioni di matrici. Ciò può anche aiutarci a vettorizzare i calcoli:

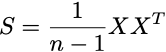
cov_mat = np.matmul(data_centered.T, data_centered)/(len(data_centered) - 1)# > array([[5.62390186, 2.47275007],# >       [2.47275007, 3.19395349]])

La ragione per passare la matrice trasposta come primo argomento nel codice è che nella formulazione matematica della matrice dei dati, le caratteristiche sono nelle righe e i soggetti nelle colonne. Nell’implementazione, accade il contrario poiché in quasi tutti i sistemi, gli eventi, i soggetti, i log, ecc., sono memorizzati nelle righe.

3. Eseguire la decomposizione in autovalori della matrice di covarianza

Gli autovalori e gli autovettori a sono calcolati usando eig() da scipy :

from scipy.linalg import eigheigvals, eigvecs = eigh(cov_mat)# Ordinamento degli autovalori e degli autovettoriindices = eigvals.argsort()[::-1]eigvals, eigvecs = eigvals[indices], eigvecs[:,indices]eigvecs# > array([[-0.82348021,  0.56734499],# >        [-0.56734499, -0.82348021]])

Come spiegato in precedenza, gli autovalori rappresentano la varianza dei componenti principali e gli autovettori sono le direzioni di proiezione:

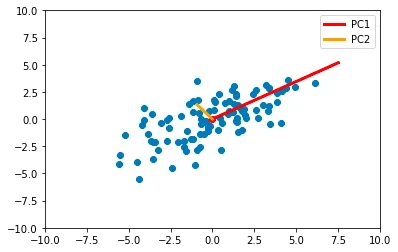
Si può vedere che viene creato un nuovo sistema di coordinate utilizzando le direzioni dei componenti principali. Inoltre, gli autovalori e gli autovettori devono essere memorizzati per trasformare i nuovi dati in seguito.

4. Applicare il determinismo

I coefficienti degli autovettori saranno sempre gli stessi, tranne per il loro segno. PCA può avere più orientamenti validi. Pertanto, dobbiamo imporre un risultato deterministico prendendo la matrice degli autovettori e per ciascuna delle sue colonne, applicando il segno del valore assoluto più grande all’interno di quella colonna.

max_abs_cols = np.argmax(np.abs(eigvecs), axis=0)signs = np.sign(eigvecs[max_abs_cols, range(eigvecs.shape[1])])eigvecs = eigvecs*signseigvecs# > array([[ 0.82348021, -0.56734499],# >      [ 0.56734499,  0.82348021]])

5. Estrarre le nuove caratteristiche

Ogni nuova caratteristica (componente principale) viene estratta eseguendo il prodotto scalare tra ogni punto nello spazio delle caratteristiche originale e l’autovettore:

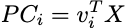
new_features = np.dot(data_centered, eigvecs)

Per questo esempio particolare, dopo aver calcolato i componenti, i nuovi punti nello spazio sono rappresentati come segue:

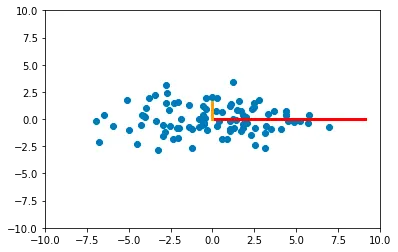
Si noti che questo risultato è essenzialmente una rotazione della nuvola di punti originale in modo che le proprietà siano non correlate.

6. Ridurre la dimensionalità

Fino ad ora, i componenti principali sono stati calcolati completamente per comprenderli, in modo visivo. Ciò che resta è scegliere quanti componenti sono necessari. Ci affidiamo agli autovalori per questo compito, poiché rappresentano la varianza di ciascun componente principale.

Il rapporto della varianza detenuta dal componente i è dato da:

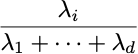
E il rapporto della varianza preservata scegliendo m componenti è dato da:

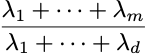
Se visualizziamo la varianza per ogni componente nel nostro esempio, otteniamo quanto segue:

# Varianza di ogni singola componente come barreplt.bar(    [f"PC_{i}" per i in range(1,len(eigvals)+1)],    eigvals/sum(eigvals))# Percentuale detenuta da m componenti come la lineaplt.plot(    [f"PC_{i}" per i in range(1,len(eigvals)+1)],    np.cumsum(eigvals)/sum(eigvals),    color='red')plt.scatter(    [f"PC_{i}" per i in range(1,len(eigvals)+1)],    np.cumsum(eigvals)/sum(eigvals),    color='red')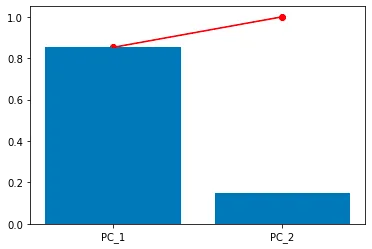

In questo caso, PC1 rappresenta l’80% della varianza dei dati originali, mentre il restante 20% appartiene a PC2. Inoltre, possiamo scegliere di utilizzare solo il primo componente principale, in tal caso i dati apparirebbero così:

Questa è la proiezione dei dati nella direzione del primo autovettore. Al momento non sembra molto utile. Cosa succederebbe invece se scegliessimo dati appartenenti a tre classi? Come apparirebbe la PCA?

PCA su dati multiclasse

Creiamo un dataset con tre classi che possano essere linearmente separabili:

from sklearn.datasets import make_blobsX, y = make_blobs()plt.scatter(X[:,0], X[:,1],c=y)plt.legend()plt.show()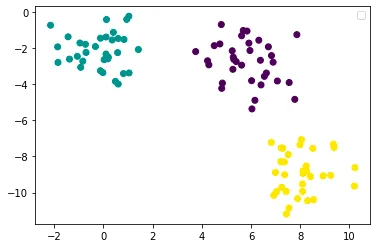

Se applichiamo la PCA ai dati sopra, questo sarebbe il grafico delle componenti principali:

E questo sarebbe il grafico della prima componente (la proiezione dei dati nella direzione dell’autovettore corrispondente all’autovalore più grande):

Funziona! I dati sembrano ancora facilmente separabili da un modello lineare.

Vantaggi e svantaggi

Come tutto nella scienza, non esiste una bacchetta magica. Ecco una lista di vantaggi e svantaggi che dovresti tenere in considerazione prima di utilizzare la PCA con dati reali.

Vantaggi di PCA

1. Riduzione della dimensionalità: PCA consente di ridurre i dati ad alta dimensionalità in uno spazio a dimensionalità inferiore preservando la maggior parte delle informazioni importanti. Ciò può essere utile per la visualizzazione dei dati, l’efficienza computazionale e per affrontare la maledizione della dimensionalità.
2. Decorrelazione: PCA trasforma le variabili originali in un nuovo insieme di variabili non correlate chiamate componenti principali. Questa decorrelazione semplifica l’analisi e può migliorare le prestazioni degli algoritmi di machine learning successivi che assumono l’indipendenza delle caratteristiche.
3. Riduzione del rumore: La rappresentazione a bassa dimensionalità ottenuta tramite PCA tende a filtrare il rumore e concentrarsi sulle variazioni più significative dei dati. Ciò può migliorare il rapporto segnale-rumore e migliorare la robustezza delle analisi successive.

Svantaggi di PCA

1. Assunzione di linearità: PCA assume che le relazioni sottostanti dei dati siano lineari. Se i dati hanno relazioni non lineari complesse, PCA potrebbe non catturare le variazioni più significative e potrebbe fornire risultati subottimali.
2. Interpretabilità: Le componenti principali ottenute da PCA sono combinazioni lineari delle caratteristiche originali. Può essere difficile correlare le componenti principali alle variabili originali e comprendere il loro significato esatto.
3. Sensibilità alla scalatura: PCA è sensibile alla scalatura delle variabili di input. Se le variabili hanno scale diverse, quelle con varianze maggiori possono dominare l’analisi, portando potenzialmente a risultati distorti. La scalatura corretta delle caratteristiche è cruciale per ottenere risultati affidabili con PCA.
4. Outliers: PCA è sensibile agli outliers poiché si concentra sulla cattura della varianza dei dati. Gli outliers possono influenzare significativamente le componenti principali e distorcere i risultati.

Implementazione di PCA fatta in casa

Ora che abbiamo trattato i dettagli dell’Analisi delle Componenti Principali, tutto ciò che resta è creare una classe che incapsula il comportamento sopra citato e che potrebbe essere riutilizzata in problemi futuri.

Per questa implementazione, verrà utilizzata l’interfaccia di scikit-learn, che ha i seguenti metodi:

• fit()
• transform()
• fit_transform()

Costruttore

Non è necessaria alcuna logica complessa. Il costruttore definirà solo il numero di componenti (caratteristiche) che avrà il dato trasformato.

import numpy as npfrom scipy.linalg import eighclass PCA:    """Analisi delle Componenti Principali.    """    def __init__(self, n_components):        """Costruttore della classe PCA.        Parametri:        ===========        n_components: int            Il numero di dimensioni per il dato trasformato.            Deve essere minore o uguale a n_features.        """        self.n_components = n_components        self._fit_instance = False

Il metodo fit

Il metodo fit applicherà i passaggi da 1 a 4 della sezione precedente.

• Centrare il dato
• Calcolare la matrice di covarianza
• Calcolare gli autovalori, gli autovettori e ordinarli
• Imporre il determinismo invertendo i segni degli autovettori

Memorizzerà anche gli autovalori e i vettori, così come la media campionaria, come attributi dell’oggetto per trasformare nuovi dati in seguito.

    def fit(self, X):        """Calcolare gli autovettori per trasformare i dati in seguito        Parametri:        ===========        X: np.array di forma [n_esempi, n_features]            La matrice dei dati                Restituisce:        ===========        Nulla        """        # Adatta la media dei dati e centrare il dato        self.mean = np.mean(X, axis=0)        X_centered = X - self.mean        # Calcola la matrice di covarianza        cov_mat = np.matmul(X_centered.T, X_centered)/(len(X_centered) - 1)        # Calcola gli autovalori, gli autovettori e li ordina        eigenvalues, eigenvectors = eigh(cov_mat)        self.eigenvalues, self.eigenvectors = self._sort_eigen(eigenvalues, eigenvectors)        # Ottieni i rapporti di varianza spiegati        self.explained_variance_ratio = self.eigenvalues/np.sum(self.eigenvalues)                # Impone il determinismo invertendo gli autovettori        self.eigenvectors = self._flip_eigenvectors(self.eigenvectors)[:, :self.n_components]        self._fit_instance = True

Il metodo di trasformazione

Applicherà i passaggi 1, 5 e 6:

• Centrando i nuovi dati utilizzando la media campionaria memorizzata
• Estrazione delle nuove caratteristiche PC
• Riduzione della dimensionalità scegliendo n_components dimensioni.

    def transform(self, X):        """Proietta i dati nelle direzioni dei vettori degli autovalori.        Parametri:        ===========        X: np.array di forma [n_esempi, n_caratteristiche]            La matrice dei dati                Returns:        ===========        pcs: np.array[n_esempi, n_components]            Le nuove caratteristiche non correlate di PCA.        """        if not self._fit_instance:            raise Exception("PCA deve essere calcolato sui dati prima! Chiamare fit()")               X_centralizzato = X - self.media        return np.dot(X_centralizzato, self.vettori_autovalori)

Il metodo fit_transform

Per la semplicità di implementazione. Questo metodo applicherà prima la funzione fit() e successivamente transform(). Sono sicuro che potrete trovare una definizione più intelligente.

def fit_transform(self, X):       """Calcola PCA e trasforma i dati.       """       self.fit(X)       return self.transform(X)

Funzioni di supporto

Questi metodi sono stati definiti come componenti separati, invece di applicare tutti i passaggi nella funzione fit() per rendere il codice più leggibile e mantenibile.

    def _flip_eigenvectors(self, vettori_autovalori):        """Forza il determinismo cambiando i segni dei vettori degli autovalori.        """        colonne_max_abs = np.argmax(np.abs(vettori_autovalori), axis=0)        segni = np.sign(vettori_autovalori[colonne_max_abs, range(vettori_autovalori.shape[1])])        return vettori_autovalori*segni        def _sort_eigen(self, autovalori, vettori_autovalori):        """Ordina gli autovalori in ordine decrescente e i loro corrispondenti vettori degli autovalori.        """        indici = autovalori.argsort()[::-1]        return autovalori[indici], vettori_autovalori[:, indici]

Test della classe

Usiamo l’esempio precedente con la nostra classe PCA:

da pca import PCA# Utilizzando la nostra implementazione di PCApca = PCA(n_components=1)X_trasformato = pca.fit_transform(X)# Tracciamento del primo PCplt.scatter(X_trasformato[:,0], [0]*len(X_trasformato),c=y)plt.legend()plt.show()

Conclusioni

Avere molte caratteristiche con pochi dati può essere dannoso e probabilmente porterà a un overfitting. L’Analisi delle Componenti Principali è uno strumento che può aiutare a risolvere questo problema. È una tecnica di riduzione della dimensionalità che funziona trovando le direzioni di proiezione per i dati in modo che la variabilità originale sia preservata il più possibile e le caratteristiche risultanti siano scorrelate. Inoltre, può essere misurata la varianza spiegata da ciascuna nuova caratteristica, o componente principale. Quindi, l’utente può scegliere quante componenti principali e quanta varianza sono sufficienti per il compito. Infine, assicurati di conoscere i tuoi dati in anticipo, poiché PCA funziona con campioni che possono essere separati linearmente e può essere sensibile agli outlier.

Riferimenti

[1] Fernández, A. Riduzione della dimensionalità. Universidad Autónoma de Madrid. Madrid, Spagna. 2022.

[2] Berrendero, J. R. Regressione lineare con dati ad alta dimensione. Universidad Autónoma de Madrid. Madrid, Spagna. 2022.

Connettiti con me su LinkedIn!