Reti di Convoluzione Grafica Introduzione alle GNN
Reti di Convoluzione Grafica e GNN
Guida passo-passo all’utilizzo di PyTorch Geometric

Graph Neural Networks (GNN) rappresentano una delle architetture più affascinanti e in rapida evoluzione nel panorama del deep learning. Come modelli di deep learning progettati per elaborare dati strutturati come grafi, i GNN offrono una straordinaria versatilità e potenti capacità di apprendimento.
Tra i vari tipi di GNN, i Graph Convolutional Networks (GCN) si sono affermati come il modello più diffuso e ampiamente applicato. I GCN sono innovativi grazie alla loro capacità di sfruttare sia le caratteristiche di un nodo che la sua località per effettuare previsioni, offrendo un modo efficace per gestire dati strutturati come grafi.
In questo articolo, approfondiremo il funzionamento del livello GCN e spiegheremo il suo funzionamento interno. Inoltre, esploreremo la sua applicazione pratica per compiti di classificazione dei nodi, utilizzando PyTorch Geometric come strumento di scelta.
PyTorch Geometric è un’estensione specializzata di PyTorch creata appositamente per lo sviluppo e l’implementazione di GNN. È una libreria avanzata, ma facile da usare, che fornisce una suite completa di strumenti per facilitare l’apprendimento automatico basato su grafi. Per iniziare il nostro percorso, sarà necessaria l’installazione di PyTorch Geometric. Se stai usando Google Colab, PyTorch dovrebbe già essere installato, quindi tutto ciò che devi fare è eseguire alcuni comandi aggiuntivi.
- Amazon introduce riassunti di recensioni generati dall’IA
- CFXplorer Pacchetto Python per la generazione di spiegazioni contro-fattuali
- Soluzione della sfida di promozione delle immagini in ambienti multipli con ArgoCD
Tutto il codice è disponibile su Google Colab e GitHub.
!pip install torch_geometric
import torch
import numpy as np
import networkx as nx
import matplotlib.pyplot as pltOra che PyTorch Geometric è installato, esploriamo il dataset che utilizzeremo in questo tutorial.
🌐 I. Dati di grafo
I grafi sono una struttura essenziale per rappresentare le relazioni tra oggetti. Puoi incontrare dati di grafo in una moltitudine di scenari del mondo reale, come reti sociali, reti informatiche, strutture chimiche delle molecole, elaborazione del linguaggio naturale e riconoscimento delle immagini, per citarne alcuni.
In questo articolo, studieremo il famoso e molto usato dataset del club di karate di Zachary.

Il dataset del club di karate di Zachary rappresenta le relazioni formate all’interno di un club di karate, osservate da Wayne W. Zachary negli anni ’70. Si tratta di una sorta di rete sociale, in cui ogni nodo rappresenta un membro del club e gli archi tra i nodi rappresentano le interazioni che si sono verificate al di fuori dell’ambiente del club.
In questo particolare scenario, i membri del club sono divisi in quattro gruppi distinti. Il nostro compito è assegnare il gruppo corretto a ciascun membro (classificazione dei nodi), in base al loro modello di interazioni.
Importiamo il dataset con la funzione integrata di PyG e cerchiamo di capire l’oggetto Datasets che utilizza.
from torch_geometric.datasets import KarateClub
# Importa il dataset da PyTorch Geometric
dataset = KarateClub()
# Stampa le informazioni
print(dataset)
print('------------')
print(f'Numero di grafi: {len(dataset)}')
print(f'Numero di caratteristiche: {dataset.num_features}')
print(f'Numero di classi: {dataset.num_classes}')
KarateClub()
------------
Numero di grafi: 1
Numero di caratteristiche: 34
Numero di classi: 4Questo dataset ha solo 1 grafo, in cui ogni nodo ha un vettore di caratteristiche di 34 dimensioni e fa parte di una delle quattro classi (i nostri quattro gruppi). In realtà, l’oggetto Datasets può essere visto come una collezione di oggetti Data (grafo).
Possiamo esaminare ulteriormente il nostro grafo unico per saperne di più.
# Stampa il primo elemento
print(f'Grafo: {dataset[0]}')
Grafo: Data(x=[34, 34], edge_index=[2, 156], y=[34], train_mask=[34])L’oggetto Data è particolarmente interessante. Stamparlo offre un buon riassunto del grafo che stiamo studiando:
x=[34, 34]è la matrice delle caratteristiche del nodo con dimensione (numero di nodi, numero di caratteristiche). Nel nostro caso, significa che abbiamo 34 nodi (i nostri 34 membri), ogni nodo è associato a un vettore di caratteristiche di dimensione 34.edge_index=[2, 156]rappresenta la connettività del grafo (come i nodi sono collegati) con dimensione (2, numero di archi diretti).y=[34]sono le etichette vere del nodo. In questo problema, ogni nodo è assegnato a una classe (gruppo), quindi abbiamo un valore per ogni nodo.train_mask=[34]è un attributo opzionale che indica quali nodi devono essere utilizzati per l’addestramento con una lista di dichiarazioniTrueoFalse.
Stampiamo ogni di questi tensori per capire cosa contengono. Iniziamo con le caratteristiche del nodo.
data = dataset[0]
print(f'x = {data.x.shape}')print(data.x)
x = torch.Size([34, 34])tensor([[1., 0., 0., ..., 0., 0., 0.], [0., 1., 0., ..., 0., 0., 0.], [0., 0., 1., ..., 0., 0., 0.], ..., [0., 0., 0., ..., 1., 0., 0.], [0., 0., 0., ..., 0., 1., 0.], [0., 0., 0., ..., 0., 0., 1.]])Qui, la matrice delle caratteristiche del nodo x è una matrice identità: non contiene alcuna informazione rilevante sui nodi. Potrebbe contenere informazioni come età, livello di competenza, ecc. ma questo non è il caso in questo dataset. Significa che dovremo classificare i nostri nodi semplicemente guardando le loro connessioni.
Ora, stampiamo l’indice degli archi.
print(f'edge_index = {data.edge_index.shape}')print(data.edge_index)
edge_index = torch.Size([2, 156])tensor([[ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 3, 3, 3, 3, 3, 3, 4, 4, 4, 5, 5, 5, 5, 6, 6, 6, 6, 7, 7, 7, 7, 8, 8, 8, 8, 8, 9, 9, 10, 10, 10, 11, 12, 12, 13, 13, 13, 13, 13, 14, 14, 15, 15, 16, 16, 17, 17, 18, 18, 19, 19, 19, 20, 20, 21, 21, 22, 22, 23, 23, 23, 23, 23, 24, 24, 24, 25, 25, 25, 26, 26, 27, 27, 27, 27, 28, 28, 28, 29, 29, 29, 29, 30, 30, 30, 30, 31, 31, 31, 31, 31, 31, 32, 32, 32, 32, 32, 32, 32, 32, 32, 32, 32, 32, 33, 33, 33, 33, 33, 33, 33, 33, 33, 33, 33, 33, 33, 33, 33, 33, 33], [ 1, 2, 3, 4, 5, 6, 7, 8, 10, 11, 12, 13, 17, 19, 21, 31, 0, 2, 3, 7, 13, 17, 19, 21, 30, 0, 1, 3, 7, 8, 9, 13, 27, 28, 32, 0, 1, 2, 7, 12, 13, 0, 6, 10, 0, 6, 10, 16, 0, 4, 5, 16, 0, 1, 2, 3, 0, 2, 30, 32, 33, 2, 33, 0, 4, 5, 0, 0, 3, 0, 1, 2, 3, 33, 32, 33, 32, 33, 5, 6, 0, 1, 32, 33, 0, 1, 33, 32, 33, 0, 1, 32, 33, 25, 27, 29, 32, 33, 25, 27, 31, 23, 24, 31, 29, 33, 2, 23, 24, 33, 2, 31, 33, 23, 26, 32, 33, 1, 8, 32, 33, 0, 24, 25, 28, 32, 33, 2, 8, 14, 15, 18, 20, 22, 23, 29, 30, 31, 33, 8, 9, 13, 14, 15, 18, 19, 20, 22, 23, 26, 27, 28, 29, 30, 31, 32]])Nella teoria dei grafi e nell’analisi delle reti, la connettività tra i nodi viene memorizzata utilizzando una varietà di strutture dati. L’edge_index è una di queste strutture dati, in cui le connessioni del grafo vengono memorizzate in due liste (156 archi diretti, che corrispondono a 78 archi bidirezionali). Il motivo di queste due liste è che una lista memorizza i nodi sorgente, mentre la seconda identifica i nodi di destinazione.
Questo metodo è noto come formato coordinate list (COO), che è essenzialmente un modo per memorizzare in modo efficiente una matrice sparsa. Le matrici sparse sono strutture dati che memorizzano in modo efficiente matrici con una maggioranza di elementi nulli. Nel formato COO, vengono memorizzati solo gli elementi diversi da zero, risparmiando memoria e risorse computazionali.
Al contrario, un modo più intuitivo e diretto per rappresentare la connettività del grafo è attraverso una matrice di adiacenza A. Questa è una matrice quadrata in cui ogni elemento Aᵢⱼ specifica la presenza o l’assenza di un arco dal nodo i al nodo j nel grafo. In altre parole, un elemento non nullo Aᵢⱼ implica una connessione dal nodo i al nodo j, mentre uno zero indica l’assenza di una connessione diretta.
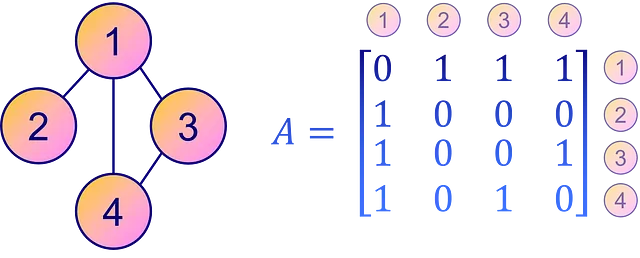
Tuttavia, una matrice di adiacenza non è altrettanto efficiente in termini di spazio come il formato COO per matrici sparse o grafi con meno archi. Tuttavia, per chiarezza e facile interpretazione, la matrice di adiacenza rimane una scelta popolare per rappresentare la connettività del grafo.
La matrice di adiacenza può essere inferita dall’edge_index con una funzione di utilità to_dense_adj().
from torch_geometric.utils import to_dense_adj
A = to_dense_adj(data.edge_index)[0].numpy().astype(int)print(f'A = {A.shape}')print(A)
A = (34, 34)[[0 1 1 ... 1 0 0] [1 0 1 ... 0 0 0] [1 1 0 ... 0 1 0] ... [1 0 0 ... 0 1 1] [0 0 1 ... 1 0 1] [0 0 0 ... 1 1 0]]Con i dati del grafo, è relativamente raro che i nodi siano densamente interconnessi. Come si può vedere, la nostra matrice di adiacenza A è sparsa (riempita di zeri).
In molti grafi reali, la maggior parte dei nodi è connessa solo ad alcuni altri nodi, il che comporta un gran numero di zeri nella matrice di adiacenza. Memorizzare così tanti zeri non è affatto efficiente, motivo per cui il formato COO è adottato da PyG.
Al contrario, le etichette di verità fondamentali sono facili da capire.
print(f'y = {data.y.shape}')print(data.y)
y = torch.Size([34])tensor([1, 1, 1, 1, 3, 3, 3, 1, 0, 1, 3, 1, 1, 1, 0, 0, 3, 1, 0, 1, 0, 1, 0, 0, 2, 2, 0, 0, 2, 0, 0, 2, 0, 0])Le nostre etichette di verità fondamentali memorizzate in y semplicemente codificano il numero di gruppo (0, 1, 2, 3) per ogni nodo, motivo per cui abbiamo 34 valori.
Infine, stampiamo la maschera di allenamento.
print(f'train_mask = {data.train_mask.shape}')print(data.train_mask)
train_mask = torch.Size([34])tensor([ True, False, False, False, True, False, False, False, True, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, True, False, False, False, False, False, False, False, False, False])La maschera di allenamento mostra quali nodi devono essere utilizzati per l’allenamento con affermazioni True. Questi nodi rappresentano l’insieme di addestramento, mentre gli altri possono essere considerati come l’insieme di test. Questa divisione aiuta nella valutazione del modello fornendo dati non visti per il testing.
Ma non abbiamo finito ancora! L’oggetto Data ha molto altro da offrire. Fornisce varie funzioni di utilità che consentono di esaminare diverse proprietà del grafo. Ad esempio:
is_directed()ti dice se il grafo è orientato. Un grafo orientato indica che la matrice di adiacenza non è simmetrica, cioè la direzione degli archi conta nelle connessioni tra i nodi.isolated_nodes()controlla se alcuni nodi non sono connessi al resto del grafo. Questi nodi sono probabilmente una sfida nelle attività come la classificazione a causa della loro mancanza di connessioni.has_self_loops()indica se almeno un nodo è connesso a se stesso. Questo è diverso dal concetto di loop: un loop implica un percorso che inizia e finisce nello stesso nodo, attraversando altri nodi nel mezzo.
Nel contesto del dataset del club di karate di Zachary, tutte queste proprietà restituiscono False. Ciò implica che il grafo non è orientato, non ha nodi isolati e nessuno dei suoi nodi è connesso a se stesso.
print(f'Gli archi sono orientati: {data.is_directed()}')print(f'Il grafo ha nodi isolati: {data.has_isolated_nodes()}')print(f'Il grafo ha loop: {data.has_self_loops()}')
Gli archi sono orientati: FalseIl grafo ha nodi isolati: FalseIl grafo ha loop: FalseInfine, possiamo convertire un grafo da PyTorch Geometric alla popolare libreria di grafi NetworkX utilizzando to_networkx. Questo è particolarmente utile per visualizzare un piccolo grafo con networkx e matplotlib.
Plottiamo il nostro dataset con un colore diverso per ogni gruppo.
from torch_geometric.utils import to_networkx
G = to_networkx(data, to_undirected=True)plt.figure(figsize=(12,12))plt.axis('off')nx.draw_networkx(G, pos=nx.spring_layout(G, seed=0), with_labels=True, node_size=800, node_color=data.y, cmap="hsv", vmin=-2, vmax=3, width=0.8, edge_color="grey", font_size=14 )plt.show()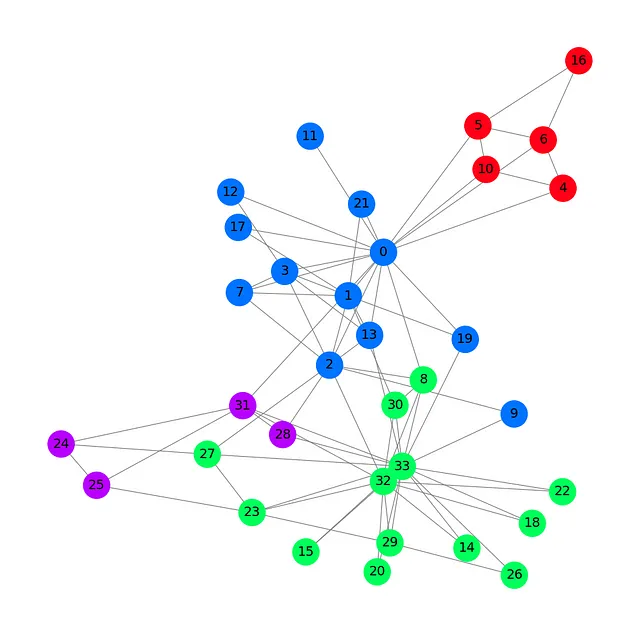
Questo grafico del club di karate di Zachary mostra i nostri 34 nodi, 78 archi (bidirezionali) e 4 etichette con 4 colori diversi. Ora che abbiamo visto gli elementi essenziali del caricamento e della gestione di un dataset con PyTorch Geometric, possiamo introdurre l’architettura delle reti neurali convoluzionali sui grafi.
✉️ II. Reti neurali convoluzionali sui grafi
Questa sezione ha lo scopo di introdurre e costruire il livello di convoluzione sui grafi da zero.
Nelle reti neurali tradizionali, i livelli lineari applicano una trasformazione lineare ai dati in ingresso. Questa trasformazione converte le caratteristiche di input x in vettori nascosti h tramite l’uso di una matrice di pesi 𝐖. Ignorando i bias per il momento, questo può essere espresso come:
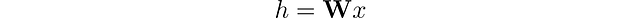
Con i dati dei grafi, viene aggiunto un ulteriore livello di complessità attraverso le connessioni tra i nodi. Queste connessioni sono importanti perché, tipicamente, nelle reti si assume che i nodi simili siano più propensi a essere collegati tra loro rispetto a quelli dissimili, un fenomeno noto come omofilia nella rete.
Possiamo arricchire la rappresentazione del nodo fondendo le sue caratteristiche con quelle dei suoi vicini. Questa operazione viene chiamata convoluzione o aggregazione del vicinato. Rappresentiamo il vicinato del nodo i incluso se stesso come Ñ.
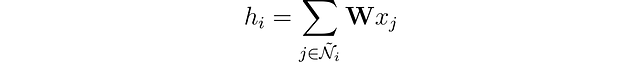
A differenza dei filtri nelle reti neurali convoluzionali (CNN), la nostra matrice di pesi 𝐖 è unica e condivisa tra ogni nodo. Ma c’è un altro problema: i nodi non hanno un numero fisso di vicini come i pixel.
Come affrontiamo i casi in cui un nodo ha solo un vicino e un altro ne ha 500? Se semplicemente sommiamo i vettori delle caratteristiche, l’embedding risultante h sarà molto più grande per il nodo con 500 vicini. Per garantire un intervallo simile di valori per tutti i nodi e la comparabilità tra di essi, possiamo normalizzare il risultato in base al grado dei nodi, dove il grado si riferisce al numero di connessioni che un nodo ha.
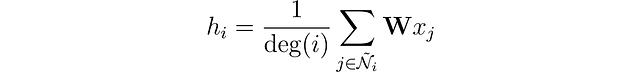
Ci siamo quasi! Introdotto da Kipf et al. (2016), il livello di convoluzione del grafo ha un ultimo miglioramento.
Gli autori hanno osservato che le caratteristiche dei nodi con numerosi vicini si propagano molto più facilmente rispetto a quelle dei nodi più isolati. Per compensare questo effetto, hanno suggerito di assegnare pesi maggiori alle caratteristiche dei nodi con meno vicini, bilanciando così l’influenza su tutti i nodi. Questa operazione è scritta come:
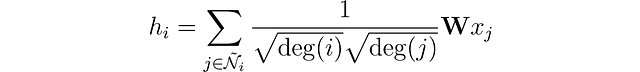
Si noti che quando i e j hanno lo stesso numero di vicini, è equivalente al nostro stesso livello. Ora vediamo come implementarlo in Python con PyTorch Geometric.
🧠 III. Implementazione di un GCN
PyTorch Geometric fornisce la funzione GCNConv, che implementa direttamente il livello di convoluzione del grafo.
In questo esempio, creeremo una rete convoluzionale grafica di base con un singolo livello GCN, una funzione di attivazione ReLU e un livello di output lineare. Questo livello di output restituirà quattro valori corrispondenti alle nostre quattro categorie, con il valore più alto che determina la classe di ciascun nodo.
Nel blocco di codice seguente, definiamo il livello GCN con un livello nascosto tridimensionale.
from torch.nn import Linearfrom torch_geometric.nn import GCNConv
class GCN(torch.nn.Module): def __init__(self): super().__init__() self.gcn = GCNConv(dataset.num_features, 3) self.out = Linear(3, dataset.num_classes) def forward(self, x, edge_index): h = self.gcn(x, edge_index).relu() z = self.out(h) return h, zmodel = GCN()print(model)
GCN( (gcn): GCNConv(34, 3) (out): Linear(in_features=3, out_features=4, bias=True))Se aggiungessimo un secondo livello GCN, il nostro modello non solo aggregerebbe i vettori delle caratteristiche dai vicini di ogni nodo, ma anche dai vicini di questi vicini.
Possiamo impilare diversi livelli di grafo per aggregare valori sempre più distanti, ma c’è un problema: se aggiungiamo troppi livelli, l’aggregazione diventa così intensa che tutti gli embedding finiscono per assomigliarsi. Questo fenomeno è chiamato sovra-smoothing e può essere un vero problema quando si hanno troppi livelli.
Ora che abbiamo definito la nostra GNN, scriviamo un semplice ciclo di addestramento con PyTorch. Ho scelto una perdita di entropia incrociata regolare poiché si tratta di un compito di classificazione multi-classe, con Adam come ottimizzatore. In questo articolo, non implementeremo una divisione tra addestramento/test per mantenere le cose semplici e concentrarci su come imparano le GNN.
Il ciclo di addestramento è standard: cerchiamo di prevedere le etichette corrette e confrontiamo i risultati del GCN con i valori memorizzati in data.y. L’errore viene calcolato dalla perdita di entropia incrociata e retropropagato con Adam per ottimizzare i pesi e i bias della nostra GNN. Infine, stampiamo le metriche ogni 10 epoche.
criterion = torch.nn.CrossEntropyLoss()optimizer = torch.optim.Adam(model.parameters(), lr=0.02)
# Calcola l'accuratezzadef accuracy(pred_y, y): return (pred_y == y).sum() / len(y)# Dati per le animazioniembeddings = []losses = []accuracies = []outputs = []# Ciclo di addestramentofor epoch in range(201): # Azzerare i gradienti optimizer.zero_grad() # Passaggio in avanti h, z = model(data.x, data.edge_index) # Calcola la funzione di perdita loss = criterion(z, data.y) # Calcola l'accuratezza acc = accuracy(z.argmax(dim=1), data.y) # Calcola i gradienti loss.backward() # Regola i parametri optimizer.step() # Memorizza i dati per le animazioni embeddings.append(h) losses.append(loss) accuracies.append(acc) outputs.append(z.argmax(dim=1)) # Stampa le metriche ogni 10 epoche if epoch % 10 == 0: print(f'Epoch {epoch:>3} | Loss: {loss:.2f} | Acc: {acc*100:.2f}%')
Epoch 0 | Loss: 1.40 | Acc: 41.18%Epoch 10 | Loss: 1.21 | Acc: 47.06%Epoch 20 | Loss: 1.02 | Acc: 67.65%Epoch 30 | Loss: 0.80 | Acc: 73.53%Epoch 40 | Loss: 0.59 | Acc: 73.53%Epoch 50 | Loss: 0.39 | Acc: 94.12%Epoch 60 | Loss: 0.23 | Acc: 97.06%Epoch 70 | Loss: 0.13 | Acc: 100.00%Epoch 80 | Loss: 0.07 | Acc: 100.00%Epoch 90 | Loss: 0.05 | Acc: 100.00%Epoch 100 | Loss: 0.03 | Acc: 100.00%Epoch 110 | Loss: 0.02 | Acc: 100.00%Epoch 120 | Loss: 0.02 | Acc: 100.00%Epoch 130 | Loss: 0.02 | Acc: 100.00%Epoch 140 | Loss: 0.01 | Acc: 100.00%Epoch 150 | Loss: 0.01 | Acc: 100.00%Epoch 160 | Loss: 0.01 | Acc: 100.00%Epoch 170 | Loss: 0.01 | Acc: 100.00%Epoch 180 | Loss: 0.01 | Acc: 100.00%Epoch 190 | Loss: 0.01 | Acc: 100.00%Epoch 200 | Loss: 0.01 | Acc: 100.00%Grande! Senza molte sorprese, raggiungiamo una precisione del 100% sul set di addestramento (dataset completo). Ciò significa che il nostro modello ha imparato ad assegnare correttamente ogni membro del club di karate al suo gruppo corretto.
Possiamo produrre una visualizzazione ordinata animando il grafo e osservando l’evoluzione delle predizioni del GNN durante il processo di addestramento.
%%capturefrom IPython.display import HTMLfrom matplotlib import animationplt.rcParams["animation.bitrate"] = 3000
def animate(i): G = to_networkx(data, to_undirected=True) nx.draw_networkx(G, pos=nx.spring_layout(G, seed=0), with_labels=True, node_size=800, node_color=outputs[i], cmap="hsv", vmin=-2, vmax=3, width=0.8, edge_color="grey", font_size=14 ) plt.title(f'Epoch {i} | Loss: {losses[i]:.2f} | Acc: {accuracies[i]*100:.2f}%', fontsize=18, pad=20)fig = plt.figure(figsize=(12, 12))plt.axis('off')anim = animation.FuncAnimation(fig, animate, \ np.arange(0, 200, 10), interval=500, repeat=True)html = HTML(anim.to_html5_video())display(html)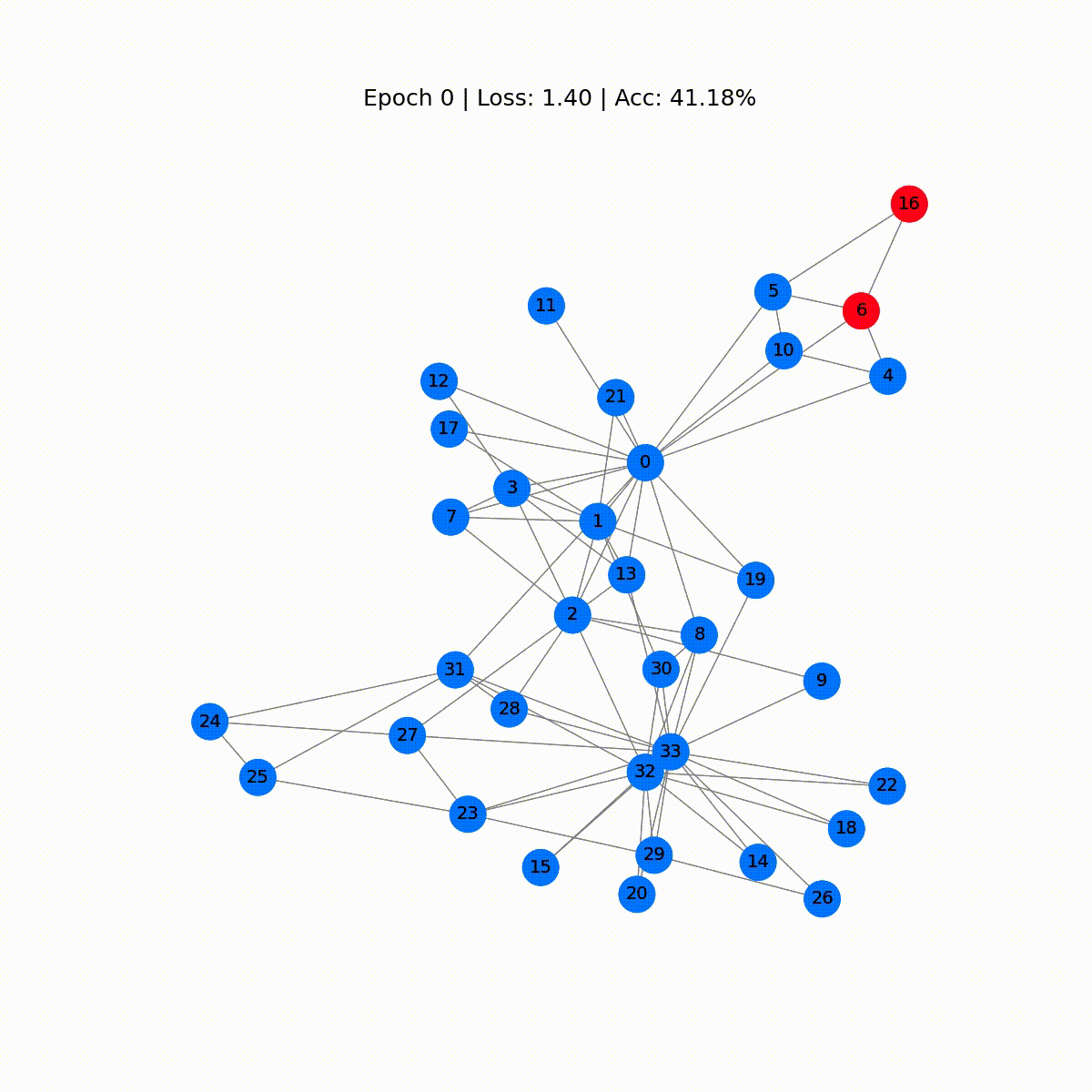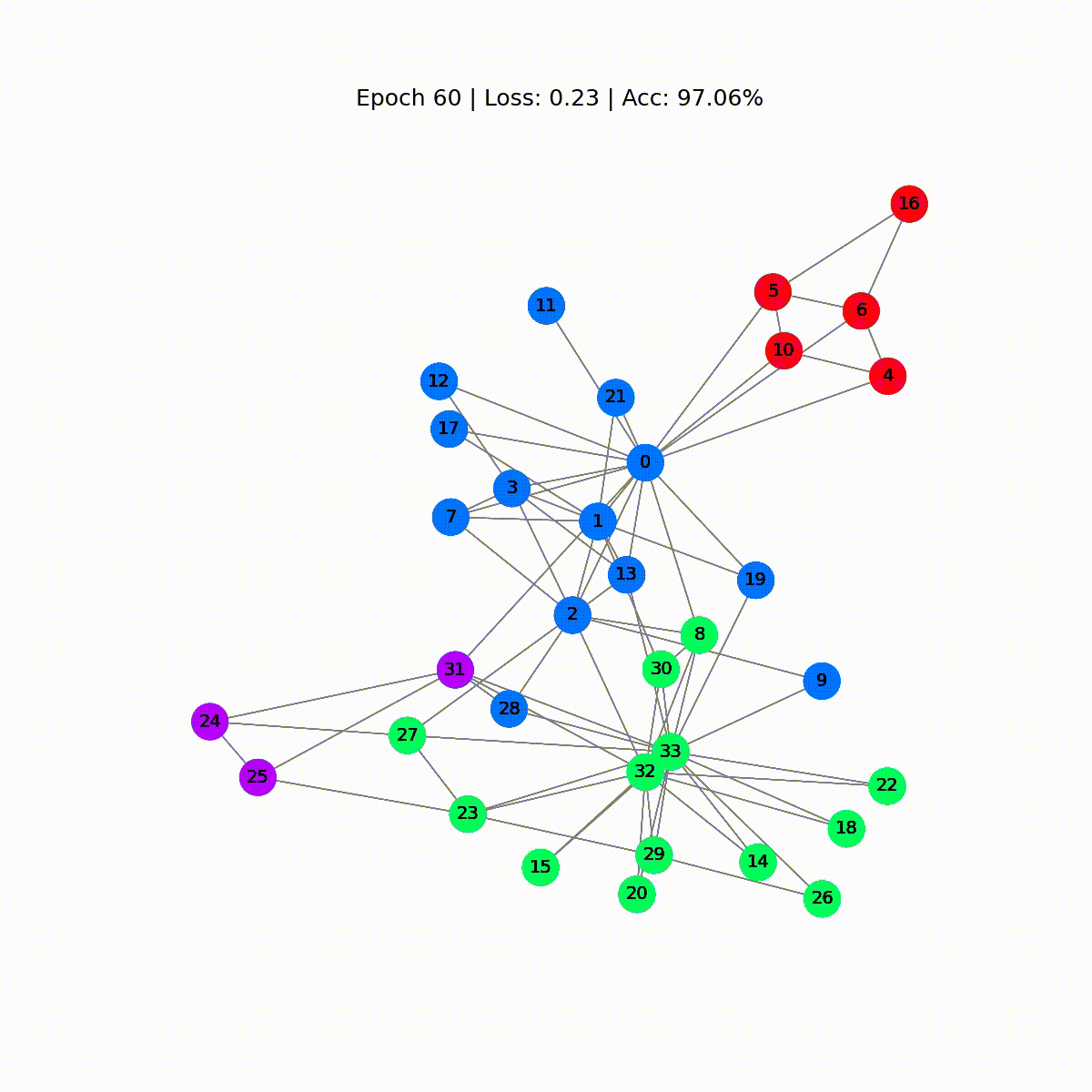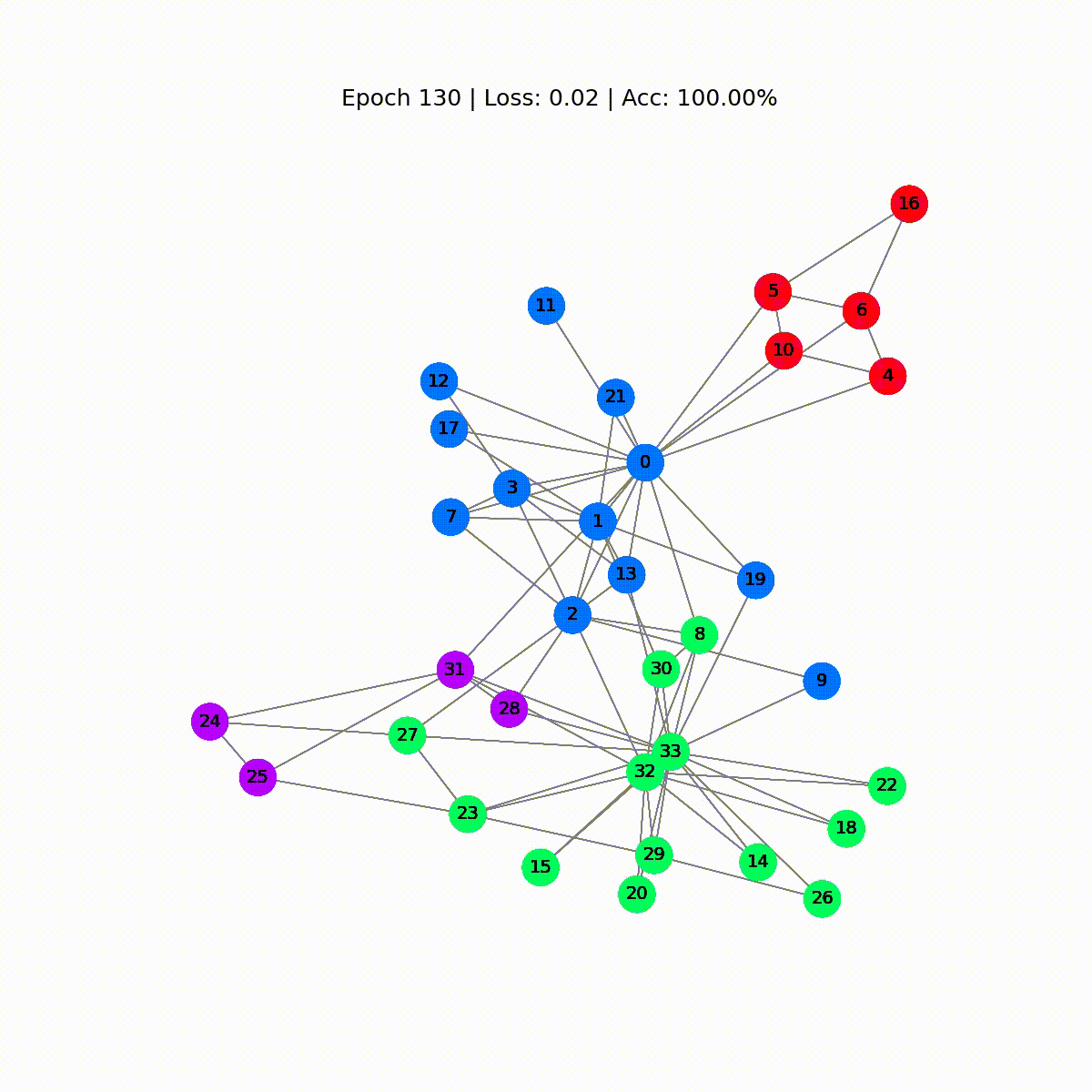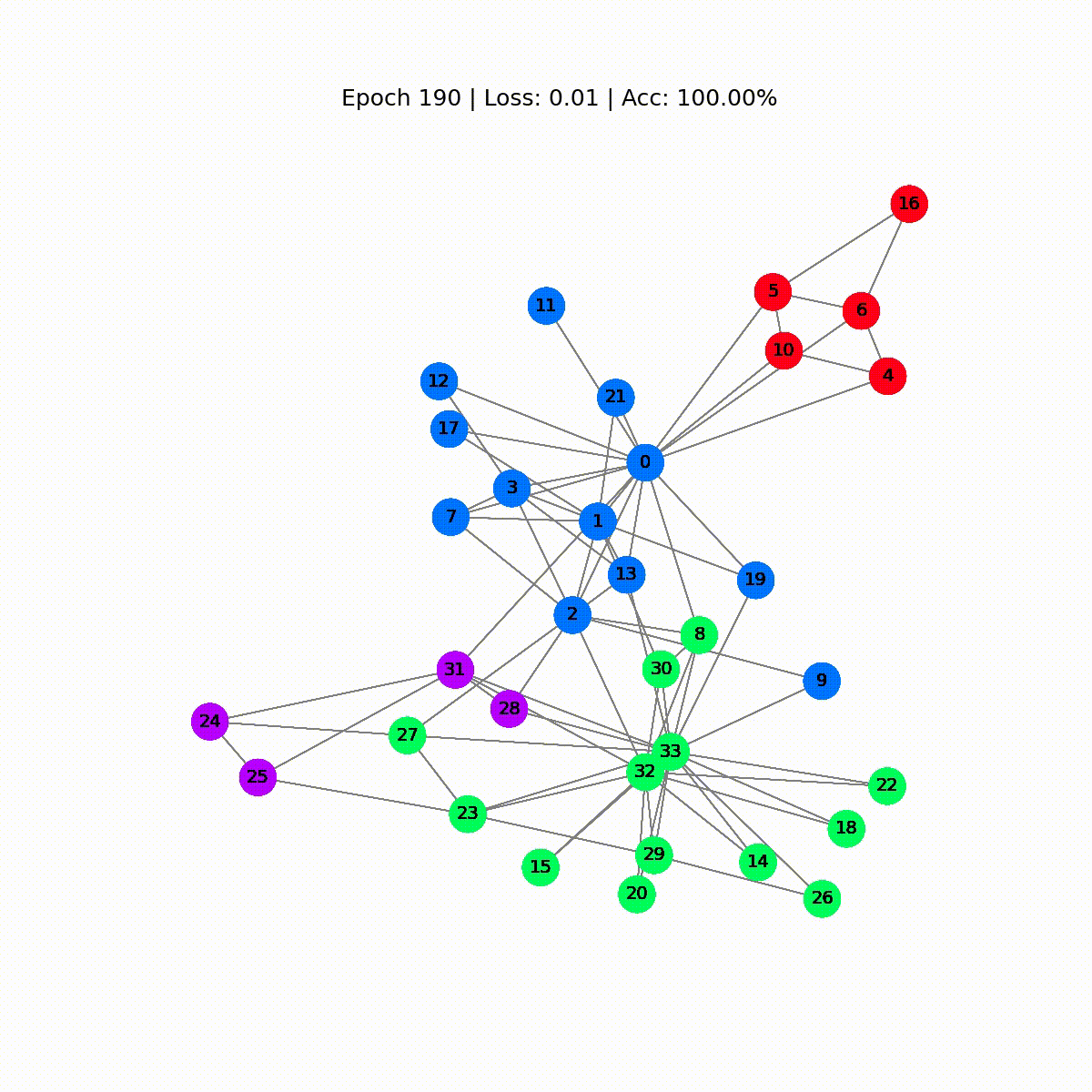
Le prime previsioni sono casuali, ma il GCN etichetta perfettamente ogni nodo dopo un po’ di tempo. Infatti, il grafo finale è lo stesso che abbiamo tracciato alla fine della prima sezione. Ma cosa impara realmente il GCN?
Aggregando le caratteristiche dei nodi vicini, il GNN apprende una rappresentazione vettoriale (o embedding) di ogni nodo nella rete. Nel nostro modello, lo strato finale impara semplicemente come utilizzare queste rappresentazioni per produrre le migliori classificazioni. Tuttavia, gli embeddings sono i veri prodotti dei GNN.
Stampiamo gli embeddings appresi dal nostro modello.
# Stampa gli embeddingsprint(f'Embeddings finali = {h.shape}')print(h)
Embeddings finali = torch.Size([34, 3])tensor([[1.9099e+00, 2.3584e+00, 7.4027e-01], [2.6203e+00, 2.7997e+00, 0.0000e+00], [2.2567e+00, 2.2962e+00, 6.4663e-01], [2.0802e+00, 2.8785e+00, 0.0000e+00], [0.0000e+00, 0.0000e+00, 2.9694e+00], [0.0000e+00, 0.0000e+00, 3.3817e+00], [0.0000e+00, 1.5008e-04, 3.4246e+00], [1.7593e+00, 2.4292e+00, 2.4551e-01], [1.9757e+00, 6.1032e-01, 1.8986e+00], [1.7770e+00, 1.9950e+00, 6.7018e-01], [0.0000e+00, 1.1683e-04, 2.9738e+00], [1.8988e+00, 2.0512e+00, 2.6225e-01], [1.7081e+00, 2.3618e+00, 1.9609e-01], [1.8303e+00, 2.1591e+00, 3.5906e-01], [2.0755e+00, 2.7468e-01, 1.9804e+00], [1.9676e+00, 3.7185e-01, 2.0011e+00], [0.0000e+00, 0.0000e+00, 3.4787e+00], [1.6945e+00, 2.0350e+00, 1.9789e-01], [1.9808e+00, 3.2633e-01, 2.1349e+00], [1.7846e+00, 1.9585e+00, 4.8021e-01], [2.0420e+00, 2.7512e-01, 1.9810e+00], [1.7665e+00, 2.1357e+00, 4.0325e-01], [1.9870e+00, 3.3886e-01, 2.0421e+00], [2.0614e+00, 5.1042e-01, 2.4872e+00],... [2.1778e+00, 4.4730e-01, 2.0077e+00], [3.8906e-02, 2.3443e+00, 1.9195e+00], [3.0748e+00, 0.0000e+00, 3.0789e+00], [3.4316e+00, 1.9716e-01, 2.5231e+00]], grad_fn=<ReluBackward0>)Come puoi vedere, gli embedding non devono avere le stesse dimensioni dei vettori delle caratteristiche. Qui ho scelto di ridurre il numero di dimensioni da 34 (dataset.num_features) a tre per ottenere una bella visualizzazione in 3D.
Plottiamo questi embedding prima che avvenga qualsiasi addestramento, all’epoca 0.
# Ottieni il primo embedding all'epoca = 0
embed = h.detach().cpu().numpy()
fig = plt.figure(figsize=(12, 12))
ax = fig.add_subplot(projection='3d')
ax.patch.set_alpha(0)
plt.tick_params(left=False,
bottom=False,
labelleft=False,
labelbottom=False)
ax.scatter(embed[:, 0], embed[:, 1], embed[:, 2],
s=200, c=data.y, cmap="hsv", vmin=-2, vmax=3)
plt.show()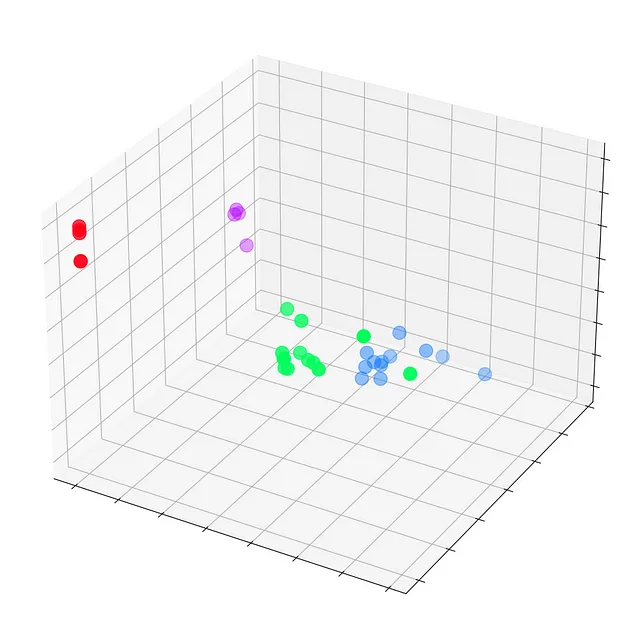
Vediamo ogni nodo del club di karate di Zachary con le loro etichette vere (e non le previsioni del modello). Per ora, sono sparsi ovunque poiché il GNN non è ancora addestrato. Ma se plottiamo questi embedding ad ogni passo del ciclo di addestramento, saremmo in grado di visualizzare ciò che il GNN impara veramente.
Vediamo come evolvono nel tempo, man mano che il GCN diventa sempre migliore nel classificare i nodi.
%%capture
def animate(i):
embed = embeddings[i].detach().cpu().numpy()
ax.clear()
ax.scatter(embed[:, 0], embed[:, 1], embed[:, 2],
s=200, c=data.y, cmap="hsv", vmin=-2, vmax=3)
plt.title(f'Epoca {i} | Loss: {losses[i]:.2f} | Acc: {accuracies[i]*100:.2f}%',
fontsize=18, pad=40)
fig = plt.figure(figsize=(12, 12))
plt.axis('off')
ax = fig.add_subplot(projection='3d')
plt.tick_params(left=False,
bottom=False,
labelleft=False,
labelbottom=False)
anim = animation.FuncAnimation(fig, animate,
np.arange(0, 200, 10), interval=800, repeat=True)
html = HTML(anim.to_html5_video())
display(html)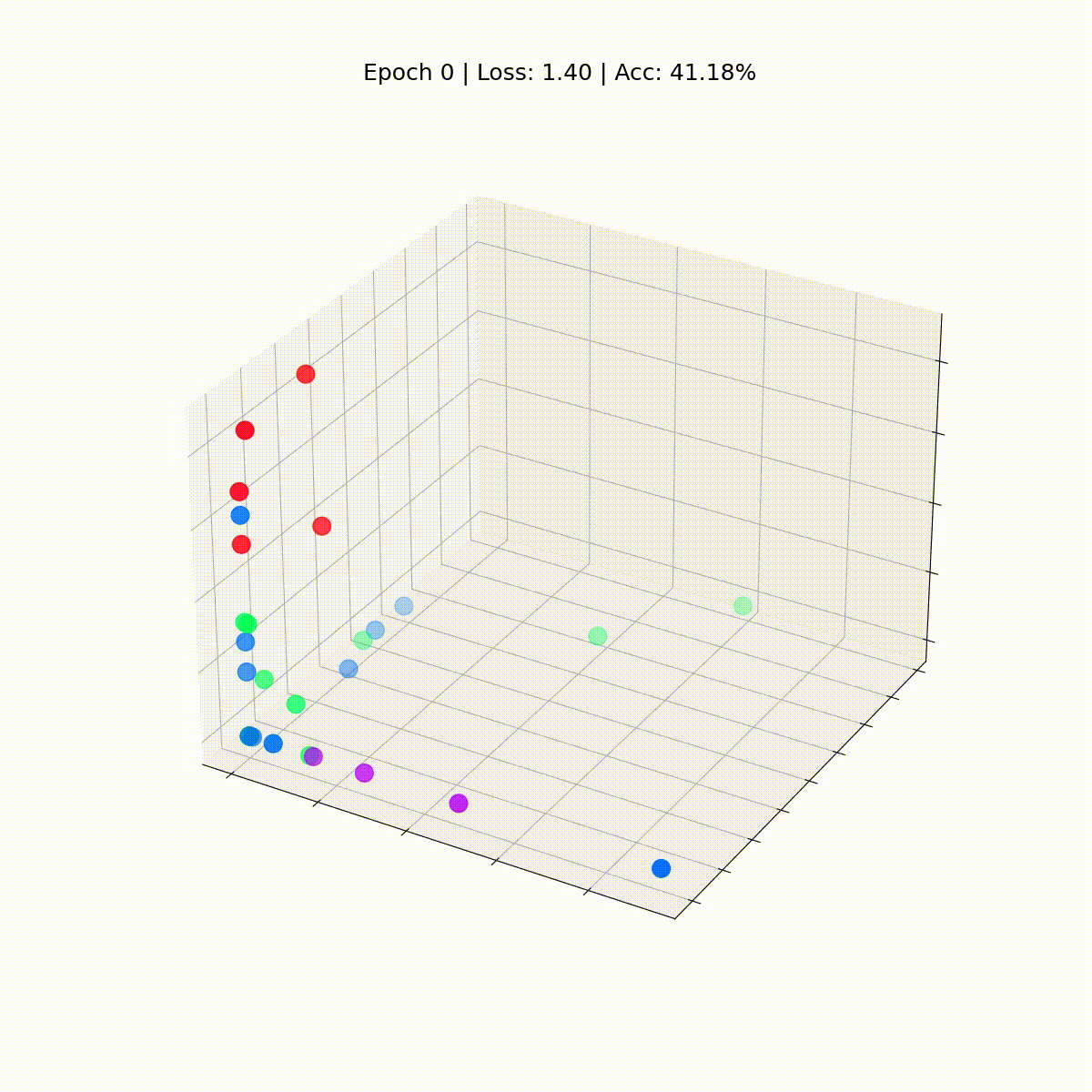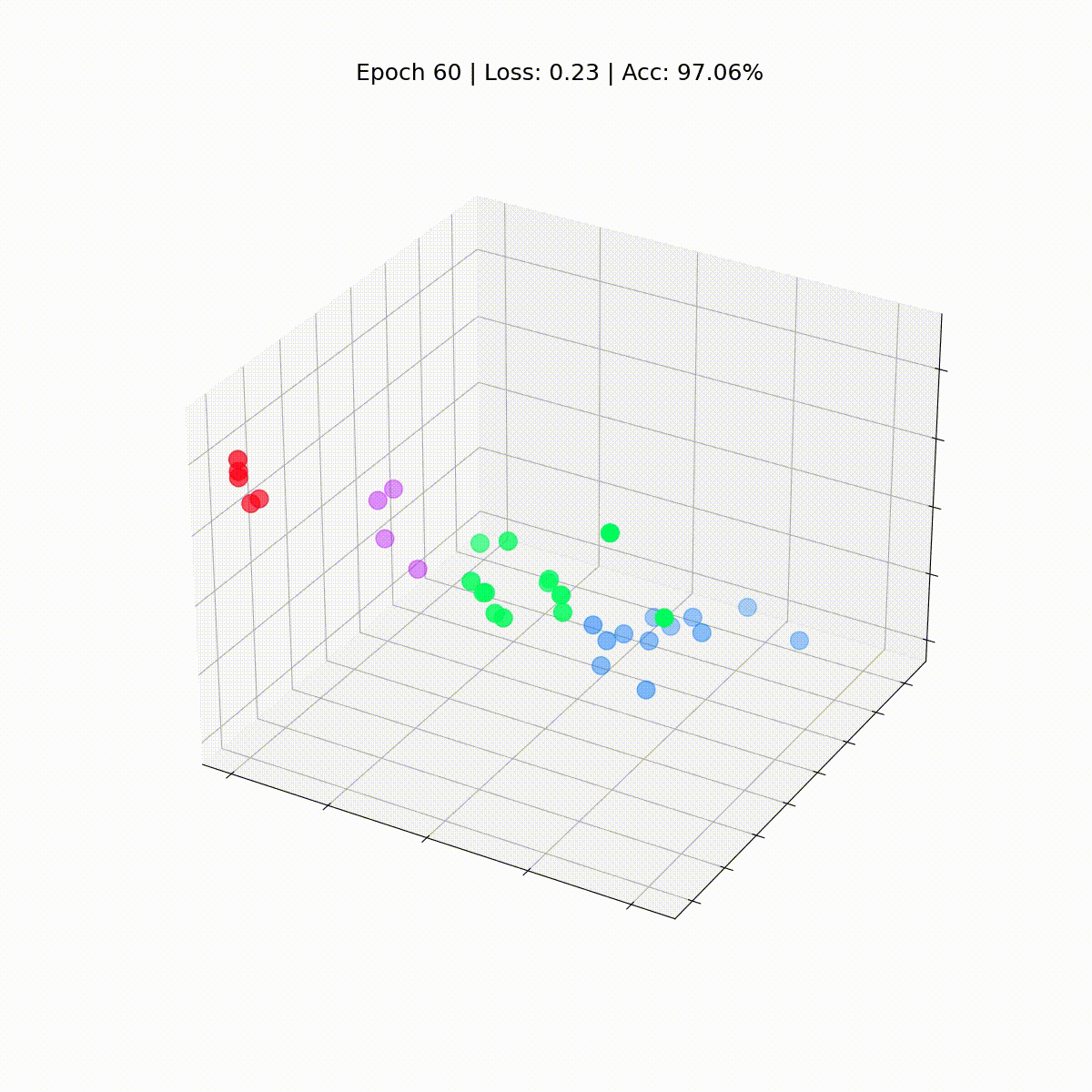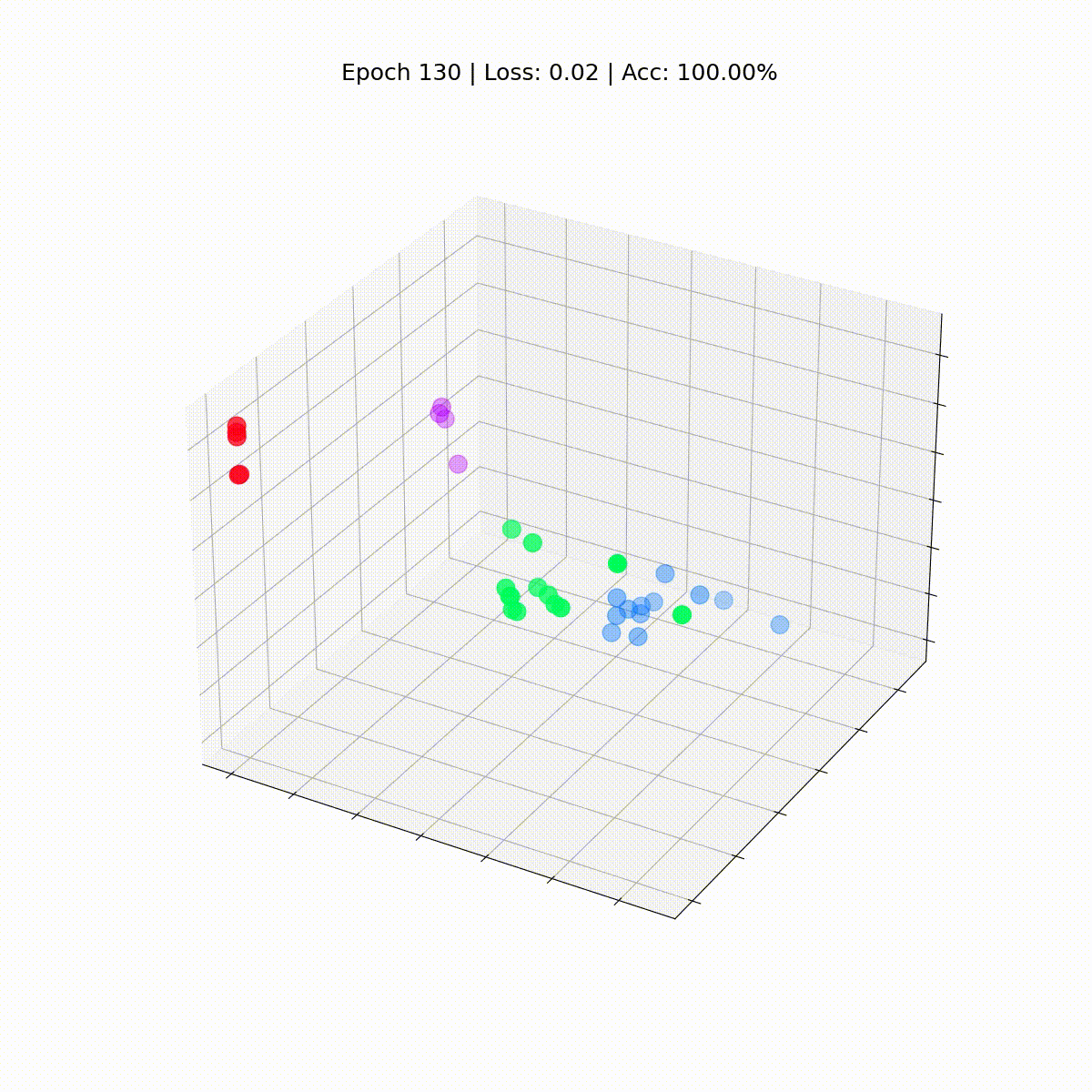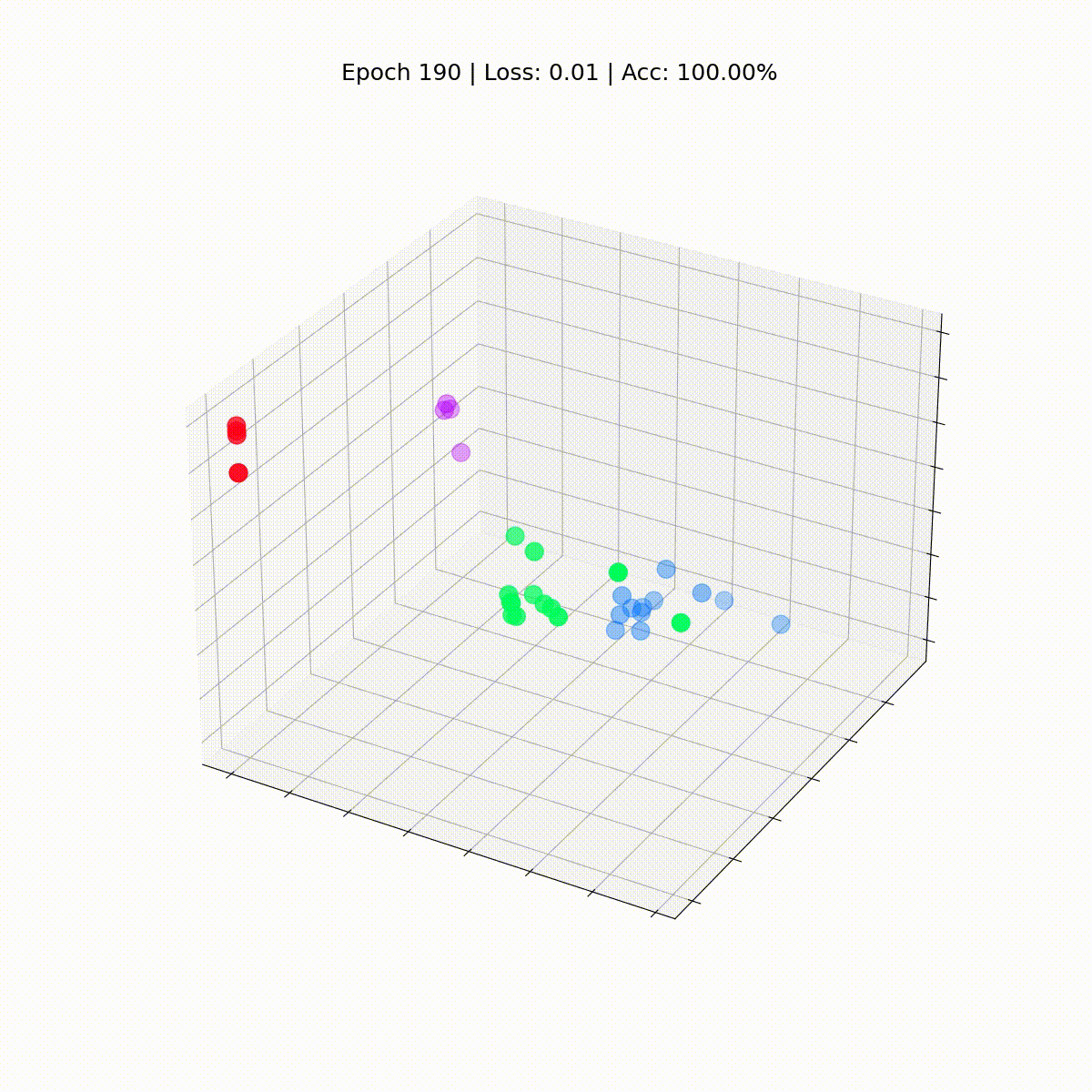
La nostra Graph Convolutional Network (GCN) ha appreso efficacemente degli embedding che raggruppano nodi simili in cluster distinti. Ciò consente al livello lineare finale di distinguerli in classi separate con facilità.
Gli embedding non sono unici per i GNN: si possono trovare ovunque nell’apprendimento profondo. Non devono essere necessariamente in 3D: in realtà, raramente lo sono. Ad esempio, i modelli di linguaggio come BERT producono embedding con 768 o addirittura 1024 dimensioni.
Dimensioni aggiuntive conservano più informazioni su nodi, testo, immagini, ecc., ma creano anche modelli più grandi che sono più difficili da addestrare. Ecco perché mantenere embedding a bassa dimensionalità il più a lungo possibile è vantaggioso.
Conclusioni
Le Graph Convolutional Networks sono un’architettura incredibilmente versatile che può essere applicata in molteplici contesti. In questo articolo, ci siamo familiarizzati con la libreria PyTorch Geometric e gli oggetti come Datasets e Data. Successivamente, abbiamo ricostruito con successo uno strato di convoluzione grafica da zero. Successivamente, abbiamo messo in pratica la teoria implementando un GCN, il che ci ha dato una comprensione degli aspetti pratici e di come interagiscono i singoli componenti. Infine, abbiamo visualizzato il processo di addestramento e ottenuto una chiara prospettiva di ciò che comporta per una tale rete.
Il club di karate di Zachary è un dataset semplice, ma è abbastanza buono per comprendere i concetti più importanti nei dati grafici e nei GNN. Sebbene abbiamo parlato solo della classificazione dei nodi in questo articolo, ci sono altre attività che i GNN possono svolgere: previsione dei collegamenti (ad esempio, per consigliare un amico), classificazione dei grafi (ad esempio, per etichettare le molecole), generazione dei grafi (ad esempio, per creare nuove molecole) e così via.
Oltre al GCN, numerosi strati e architetture GNN sono stati proposti dai ricercatori. Nel prossimo articolo, presenteremo l’architettura Graph Attention Network (GAT), che calcola dinamicamente il fattore di normalizzazione del GCN e l’importanza di ogni connessione con un meccanismo di attenzione.
Se vuoi saperne di più sui grafi neurali, approfondisci il mondo dei GNN con il mio libro, Hands-On Graph Neural Networks.
Prossimo articolo
Capitolo 2: Graph Attention Networks: Self-Attention Explained
Una guida ai GNN con auto-attenzione utilizzando PyTorch Geometric
towardsdatascience.com
Scopri di più sull’apprendimento automatico e supporta il mio lavoro con un solo clic: diventa un membro di VoAGI qui:
Unisciti a VoAGI con il mio link di riferimento – Maxime Labonne
Come membro di VoAGI, una parte della tua quota di iscrizione va agli scrittori che leggi e ottieni accesso completo ad ogni storia…
VoAGI.com
Se sei già un membro, puoi seguirmi su VoAGI.




