Regressione Lineare da Zero con NumPy
Regressione Lineare con NumPy
Motivazione
La regressione lineare è uno degli strumenti più fondamentali nell’apprendimento automatico. Viene utilizzata per trovare una linea retta che si adatta bene ai nostri dati. Anche se funziona solo con modelli semplici a linea retta, capire la matematica alla base ci aiuta a comprendere la discesa del gradiente e i metodi di minimizzazione della perdita. Questi sono importanti per modelli più complessi utilizzati in tutti i compiti di apprendimento automatico e di apprendimento profondo.
- I 5 migliori strumenti di intelligenza artificiale per massimizzare la produttività
- Utilizzo dell’OCR per disegni tecnici complessi
- Una revisione completa di Blockchain in AI
In questo articolo, ci armeremo di pazienza e costruiremo la regressione lineare da zero utilizzando NumPy. Invece di utilizzare implementazioni astratte come quelle fornite da Scikit-Learn, partiremo dalle basi.
Dataset
Generiamo un dataset fittizio utilizzando i metodi di Scikit-Learn. Per ora utilizziamo solo una variabile, ma l’implementazione sarà generale e potrà essere allenata su qualsiasi numero di features.
Il metodo make_regression fornito da Scikit-Learn genera dataset di regressione lineare casuali, con l’aggiunta di rumore gaussiano per aggiungere un po’ di casualità.
X, y = datasets.make_regression(
n_samples=500, n_features=1, noise=15, random_state=4)
Generiamo 500 valori casuali, ognuno con una singola feature. Pertanto, X ha forma (500, 1) e ciascuno dei 500 valori indipendenti di X ha un corrispondente valore y. Quindi, anche y ha forma (500, ).
Visualizzando il dataset, appare come segue:
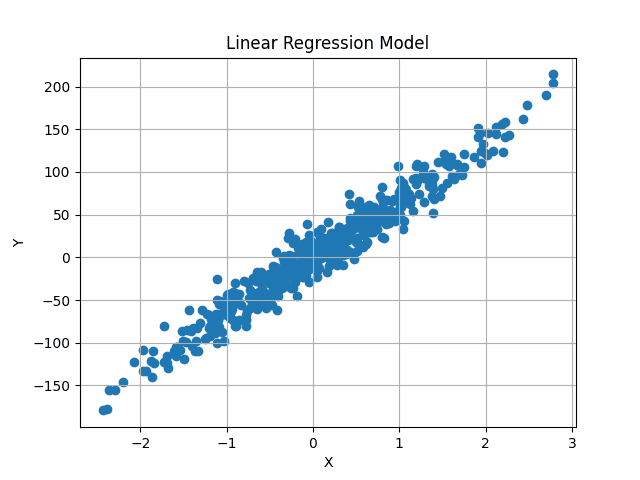
Il nostro obiettivo è trovare una linea di miglior adattamento che passi attraverso il centro di questi dati, minimizzando la differenza media tra i valori y predetti e quelli originali.
Intuizione
L’equazione generale per una linea retta è:
y = m*X + b
X è numerico, a valore singolo. Qui m e b rappresentano la pendenza e l’intercetta y (o bias). Questi sono sconosciuti e valori variabili di questi possono generare linee diverse. Nell’apprendimento automatico, X dipende dai dati, così come i valori y. Abbiamo solo controllo su m e b, che agiscono come i nostri parametri del modello. Cerchiamo di trovare valori ottimali per questi due parametri, che generano una linea che minimizza la differenza tra i valori y previsti e quelli effettivi.
Ciò si estende allo scenario in cui X è multidimensionale. In tal caso, il numero di valori m sarà uguale al numero di dimensioni dei nostri dati. Ad esempio, se i nostri dati hanno tre diverse features, avremo tre diversi valori di m, chiamati pesi.
L’equazione diventerà quindi:
y = w1*X1 + w2*X2 + w3*X3 + b
Questo può quindi estendersi a qualsiasi numero di features.
Ma come sappiamo i valori ottimali del nostro bias e dei nostri pesi? Beh, non lo sappiamo. Ma possiamo trovarlo in modo iterativo utilizzando la discesa del gradiente. Partiamo con valori casuali e li cambiamo leggermente per più passaggi fino ad avvicinarci ai valori ottimali.
Per prima cosa, iniziamo inizializzando la regressione lineare e successivamente approfondiremo il processo di ottimizzazione.
Inizializza la Classe di Regressione Lineare
import numpy as np
class LinearRegression:
def __init__(self, lr: int = 0.01, n_iters: int = 1000) -> None:
self.lr = lr
self.n_iters = n_iters
self.weights = None
self.bias = None
Utilizziamo iperparametri come il tasso di apprendimento e il numero di iterazioni, che verranno spiegati in seguito. I pesi e il bias sono impostati su None perché il numero di parametri dei pesi dipende dalle features di input all’interno dei dati. Non abbiamo ancora accesso ai dati, quindi li inizializziamo a None per ora.
Il Metodo Fit
Nel metodo fit, ci vengono forniti i dati e i loro valori associati. Possiamo ora utilizzare questi per inizializzare i nostri pesi e quindi allenare il modello per trovare i pesi ottimali.
def fit(self, X, y):
num_samples, num_features = X.shape # La forma di X è [N, f]
self.weights = np.random.rand(num_features) # La forma di W è [f, 1]
self.bias = 0
La caratteristica indipendente X sarà un array NumPy con forma (num_samples, num_features). Nel nostro caso, la forma di X sarà (500, 1). Ogni riga dei nostri dati avrà un valore target associato, quindi y avrà anche la forma (500,) o (num_samples).
Estraiamo ciò e inizializziamo casualmente i pesi dati il numero di caratteristiche di input. Quindi ora i nostri pesi sono anche un array NumPy di dimensione (num_features, ). Il bias è un singolo valore inizializzato a zero.
Previsione dei valori di Y
Utilizziamo l’equazione della linea discussa in precedenza per calcolare i valori di y previsti. Tuttavia, anziché un approccio iterativo per sommare tutti i valori, possiamo seguire un approccio vettorizzato per una computazione più veloce. Dato che i pesi e i valori di X sono array NumPy, possiamo usare la moltiplicazione matriciale per ottenere le previsioni.
X ha forma (num_samples, num_features) e i pesi hanno forma (num_features, ). Vogliamo che le previsioni abbiano forma (num_samples, ) corrispondente ai valori y originali. Pertanto, possiamo moltiplicare X per i pesi, ovvero (num_samples, num_features) x (num_features, ) per ottenere previsioni di forma (num_samples, ).
Il valore di bias viene aggiunto alla fine di ogni previsione. Ciò può essere implementato semplicemente in una sola riga.
# La forma di y_pred dovrebbe essere N, 1
y_pred = np.dot(X, self.weights) + self.bias
Tuttavia, queste previsioni sono corrette? Ovviamente no. Stiamo utilizzando valori inizializzati casualmente per i pesi e il bias, quindi le previsioni saranno anche casuali.
Come otteniamo i valori ottimali? Discesa del Gradiente.
Funzione di Loss e Discesa del Gradiente
Ora che abbiamo sia le previsioni che i valori target di y, possiamo trovare la differenza tra entrambi i valori. L’Errore Quadratico Medio (MSE) viene utilizzato per confrontare numeri reali. L’equazione è la seguente:
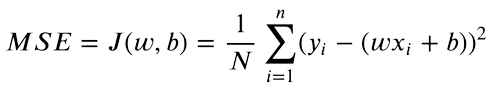
Ci interessa solo la differenza assoluta tra i nostri valori. Una previsione superiore al valore originale è tanto sbagliata quanto una previsione inferiore. Quindi eleviamo al quadrato la differenza tra il valore target e le previsioni, per convertire le differenze negative in positive. Inoltre, questo penalizza una differenza maggiore tra i target e le previsioni, poiché le differenze più grandi elevate al quadrato contribuiranno di più alla perdita finale.
Perché le nostre previsioni siano il più vicine possibile ai target originali, cerchiamo ora di minimizzare questa funzione. La funzione di loss sarà minima quando il gradiente è zero. Poiché possiamo ottimizzare solo i valori dei pesi e del bias, prendiamo le derivate parziali della funzione MSE rispetto ai valori dei pesi e del bias.
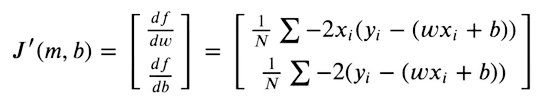
Quindi ottimizziamo i nostri pesi dati i valori del gradiente, utilizzando la Discesa del Gradiente.
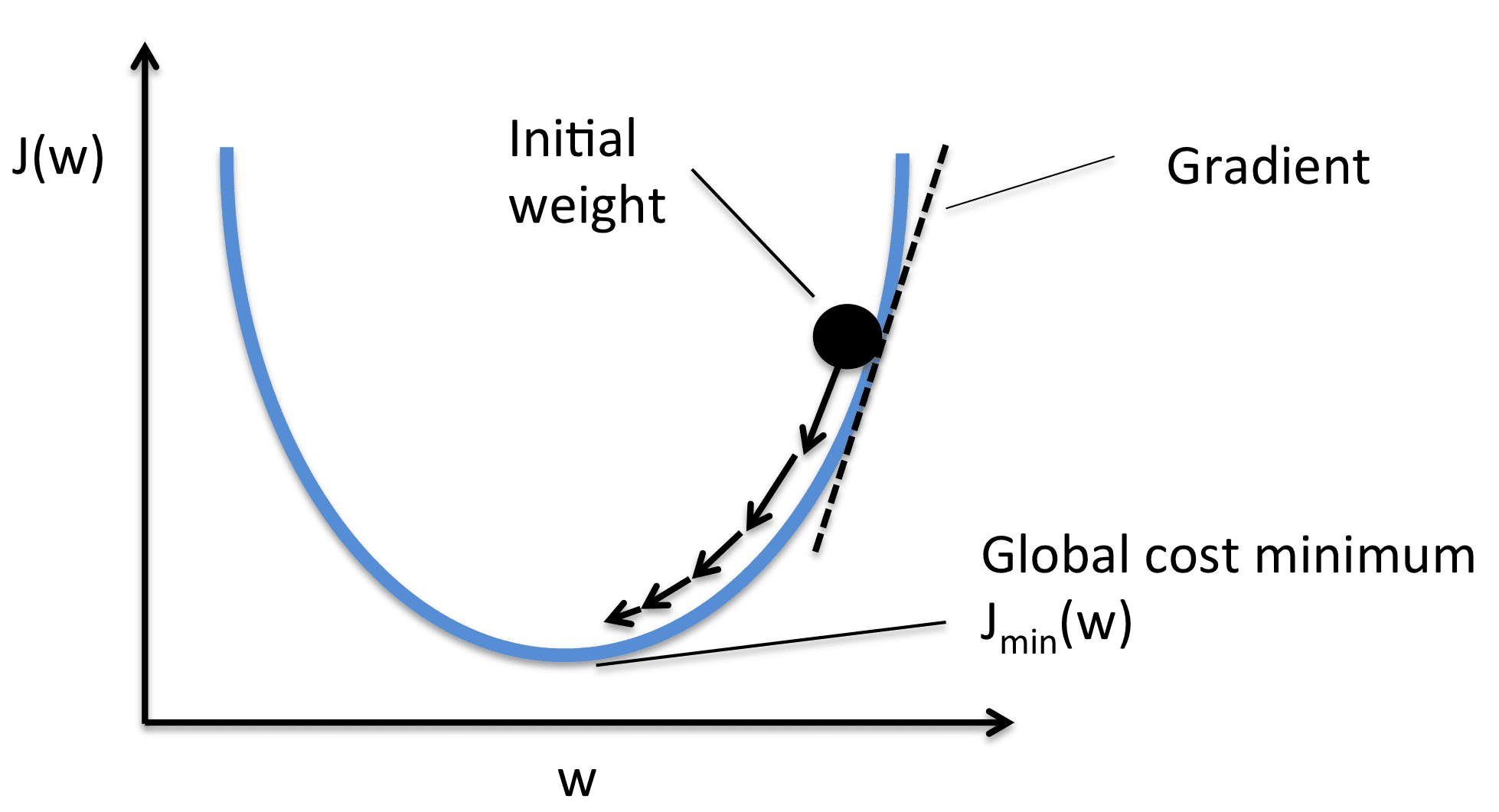
Prendiamo il gradiente rispetto a ciascun valore dei pesi e quindi li spostiamo all’opposto del gradiente. Ciò spinge la perdita verso il minimo. Come mostrato nell’immagine, il gradiente è positivo, quindi diminuiamo il peso. Ciò spinge J(W) o la perdita verso il valore minimo. Pertanto, le equazioni di ottimizzazione sono le seguenti:
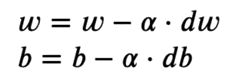
Il tasso di apprendimento (o alpha) controlla i passi incrementali mostrati nell’immagine. Facciamo solo una piccola modifica nel valore, per un movimento stabile verso il minimo.
Implementazione
Se semplifichiamo l’equazione derivata utilizzando manipolazioni algebriche di base, diventa molto semplice da implementare.
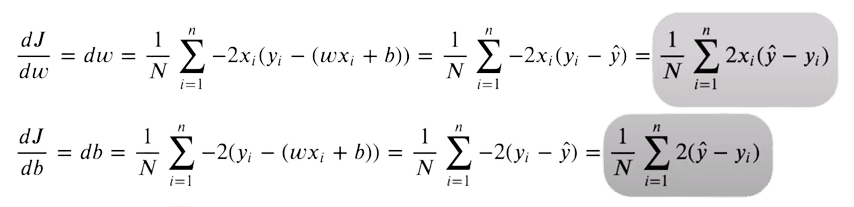
Per la derivata, implementiamo questo usando due righe di codice:
# X -> [ N, f ]
# y_pred -> [ N ]
# dw -> [ f ]
dw = (1 / num_samples) * np.dot(X.T, y_pred - y)
db = (1 / num_samples) * np.sum(y_pred - y)
dw ha di nuovo forma (num_features, ). Quindi abbiamo un valore di derivata separato per ogni peso. Li ottimizziamo separatamente. db ha un singolo valore.
Per ottimizzare i valori ora, spostiamo i valori nella direzione opposta del gradiente utilizzando una semplice sottrazione.
self.weights = self.weights - self.lr * dw
self.bias = self.bias - self.lr * db
Di nuovo, questo è solo un singolo passo. Facciamo solo una piccola modifica ai valori inizializzati casualmente. Ora eseguiamo ripetutamente gli stessi passaggi per convergere verso un minimo.
Il loop completo è il seguente:
for i in range(self.n_iters):
# y_pred la forma dovrebbe essere N, 1
y_pred = np.dot(X, self.weights) + self.bias
# X -> [N,f]
# y_pred -> [N]
# dw -> [f]
dw = (1 / num_samples) * np.dot(X.T, y_pred - y)
db = (1 / num_samples) * np.sum(y_pred - y)
self.weights = self.weights - self.lr * dw
self.bias = self.bias - self.lr * db
Predizione
Prevediamo allo stesso modo in cui abbiamo fatto durante l’addestramento. Tuttavia, ora abbiamo il set ottimale di pesi e bias. I valori previsti dovrebbero ora essere vicini ai valori originali.
def predict(self, X):
return np.dot(X, self.weights) + self.bias
Risultati
Con pesi e bias inizializzati casualmente, le nostre previsioni erano le seguenti:
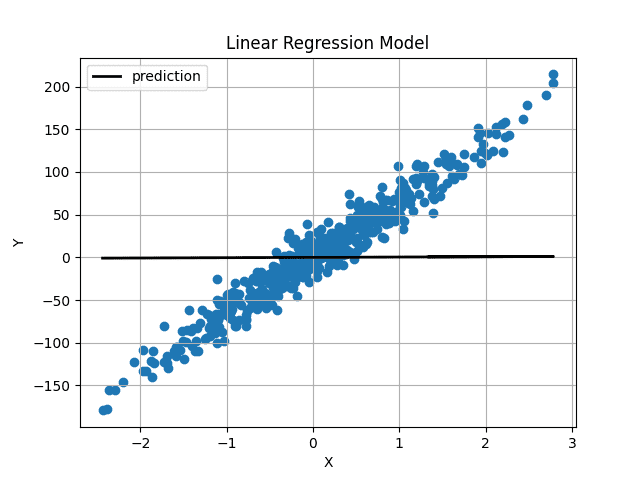Immagine dell’autore I pesi e il bias sono stati inizializzati molto vicini a 0, quindi otteniamo una linea orizzontale. Dopo aver addestrato il modello per 1000 iterazioni, otteniamo questo:
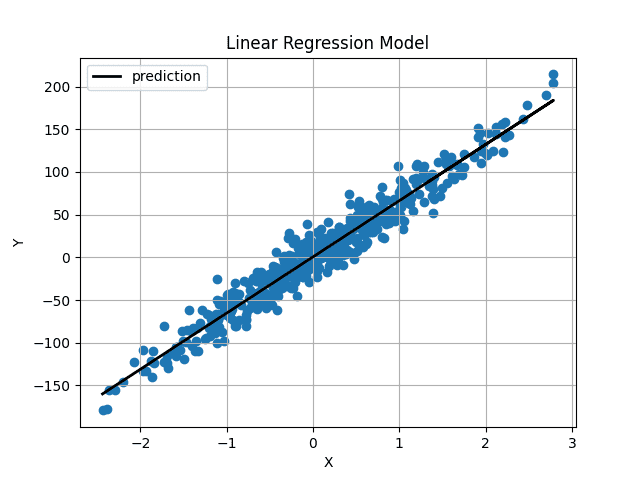Immagine dell’autore
La linea prevista passa proprio attraverso il centro dei nostri dati e sembra essere la linea migliore possibile.
Conclusione
Hai ora implementato la regressione lineare da zero. Il codice completo è anche disponibile su GitHub.
import numpy as np
class LinearRegression:
def __init__(self, lr: int = 0.01, n_iters: int = 1000) -> None:
self.lr = lr
self.n_iters = n_iters
self.weights = None
self.bias = None
def fit(self, X, y):
num_samples, num_features = X.shape # X forma [N, f]
self.weights = np.random.rand(num_features) # W forma [f, 1]
self.bias = 0
for i in range(self.n_iters):
# y_pred la forma dovrebbe essere N, 1
y_pred = np.dot(X, self.weights) + self.bias
# X -> [N,f]
# y_pred -> [N]
# dw -> [f]
dw = (1 / num_samples) * np.dot(X.T, y_pred - y)
db = (1 / num_samples) * np.sum(y_pred - y)
self.weights = self.weights - self.lr * dw
self.bias = self.bias - self.lr * db
return self
def predict(self, X):
return np.dot(X, self.weights) + self.biasMuhammad Arham è un ingegnere di Deep Learning che lavora in Visione Artificiale e Elaborazione del Linguaggio Naturale. Ha lavorato sul deployment e l’ottimizzazione di diverse applicazioni di AI generativa che hanno raggiunto le classifiche globali in Vyro.AI. È interessato alla costruzione e all’ottimizzazione di modelli di machine learning per sistemi intelligenti e crede nel miglioramento continuo.
