Simulazione 105 Modellazione del Pendolo Doppio con Integrazione Numerica

Pendulum Simulation 105 Double Pendulum Modeling with Numerical Integration

Modellare un sistema caotico

Il pendolo è un sistema di fisica classica con cui siamo tutti familiari. Che si tratti di un orologio a pendolo o di un bambino su un’altalena, abbiamo visto il moto regolare e periodico del pendolo. Un singolo pendolo è ben definito nella fisica classica, ma il pendolo doppio (un pendolo attaccato all’estremità di un altro pendolo) è letteralmente caos. In questo articolo, approfondiremo la nostra comprensione intuitiva dei pendoli e modelleremo il caos del pendolo doppio. La fisica è interessante e i metodi numerici necessari sono uno strumento essenziale nell’arsenale di chiunque.

In questo articolo:

• Impareremo il moto armonico e modelleremo il comportamento di un singolo pendolo
• Impareremo i fondamenti della teoria del caos
• Modelleremo il comportamento caotico di un pendolo doppio numericamente

Moto Armonico e Pendolo Singolo

Moto Armonico Semplice

Descriviamo il movimento oscillante periodico di un pendolo come moto armonico. Il moto armonico si verifica quando c’è un movimento in un sistema che viene bilanciato da una forza di ripristino proporzionale nella direzione opposta a tale movimento. Vediamo un esempio di ciò nella figura 2, dove una massa su una molla viene tirata verso il basso a causa della gravità, ma questo mette energia nella molla che poi si ritorce e tira la massa verso l’alto. Accanto al sistema a molla, vediamo l’altezza della massa che gira in un cerchio chiamato diagramma dei fasori, che illustra ulteriormente il moto regolare del sistema.

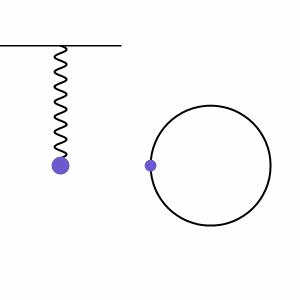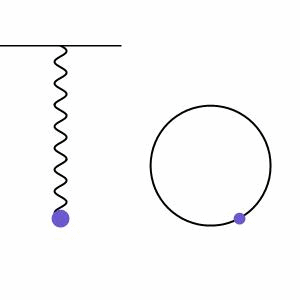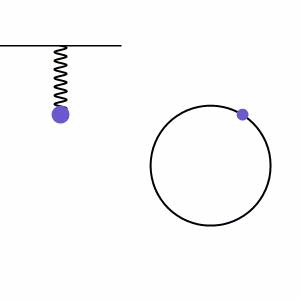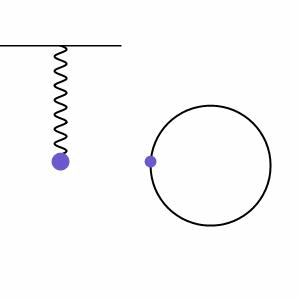
Il moto armonico può essere smorzato (diminuzione dell’ampiezza a causa delle forze di attrito) o forzato (aumento dell’ampiezza a causa di una forza esterna aggiunta), ma inizieremo con il caso più semplice di moto armonico indefinito senza forze esterne che agiscono su di esso (moto non smorzato). Questo tipo di moto è una buona approssimazione per modellare un pendolo singolo che oscilla ad un angolo piccolo/bassa ampiezza. In questo caso possiamo modellare il moto con l’equazione 1 qui sotto.

• Dominare il Test A/B Un Esempio di Business del Mondo Reale [Parte 1]
• OpenAI registra una diminuzione del traffico di quasi il 20% in 3 mesi
• Sviluppo di un sistema autonomo di chatbot duali per la sintesi di articoli di ricerca

Possiamo facilmente inserire questa funzione nel codice e simulare un pendolo semplice nel tempo.

def simple_pendulum(theta_0, omega, t, phi):    theta = theta_0*np.cos(omega*t + phi)    return theta#parametri del nostro sistematheta_0 = np.radians(15) #gradi in radianti.g = 9.8 #m/s^2l = 1.0 #momega = np.sqrt(g/l)phi = 0 #per angoli piccolitime_span = np.linspace(0,20,300) #simulazione per 20s diviso in 300 intervalli temporali.theta = []for t in time_span:    theta.append(simple_pendulum(theta_0, omega, t, phi))#Convertire nuovamente in coordinate cartesianex = l*np.sin(theta)y = -l*np.cos(theta) #negativo per assicurarsi che il pendolo sia rivolto verso il basso

Moto Completo del Pendolo con Meccanica Lagrangiana

Un semplice pendolo ad angolo ridotto è un buon punto di partenza, ma vogliamo andare oltre e modellare il movimento di un pendolo completo. Poiché non possiamo più utilizzare approssimazioni ad angolo ridotto, è meglio modellare il pendolo utilizzando la meccanica lagrangiana. Questo è uno strumento essenziale in fisica che ci porta a guardare le forze in un sistema per guardare l’energia in un sistema. Stiamo cambiando il nostro punto di vista da forza motrice vs forza di ripristino a energia cinetica vs energia potenziale.

Il Lagrangiano è la differenza tra energia cinetica ed energia potenziale data nell’equazione 2.

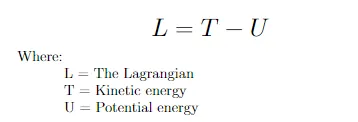
Sostituendo il Cinetico e il Potenziale di un pendolo dati nell’equazione 3 si ottiene il Lagrangiano per un pendolo visto nell’equazione 4

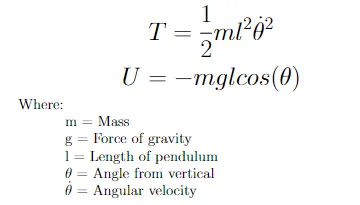
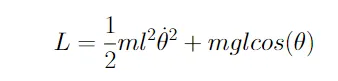
Con il Lagrangiano per un pendolo descriviamo ora l’energia del nostro sistema. C’è un ultimo passo matematico da compiere per trasformarlo in qualcosa su cui possiamo costruire una simulazione. Dobbiamo tornare al riferimento dinamico/forza orientata dal riferimento energetico utilizzando l’equazione di Euler-Lagrange. Utilizzando questa equazione possiamo utilizzare il Lagrangiano per ottenere l’accelerazione angolare del nostro pendolo.

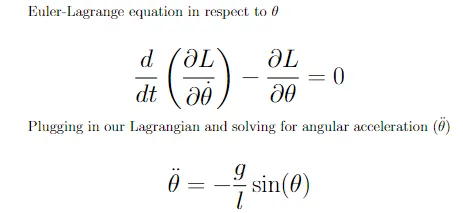
Dopo aver eseguito i calcoli, otteniamo l’accelerazione angolare che possiamo utilizzare per ottenere la velocità angolare e l’angolo stesso. Ciò richiederà un’integrazione numerica che verrà illustrata nella nostra simulazione completa del pendolo. Anche per un singolo pendolo, la dinamica non lineare significa che non esiste una soluzione analitica per risolvere theta, quindi la necessità di una soluzione numerica. L’integrazione è piuttosto semplice (ma potente), utilizziamo l’accelerazione angolare per aggiornare la velocità angolare e la velocità angolare per aggiornare theta aggiungendo la prima quantità alla seconda e moltiplicando il tutto per un certo intervallo di tempo. Questo ci fornisce un’approssimazione dell’area sotto la curva accelerazione/velocità. Più piccolo è l’intervallo di tempo, più accurata è l’approssimazione.

def pendolo_completo(g,l,theta,theta_velocità, intervallo_temporale):    #Integrazione numerica    accelerazione_angolare = -(g/l)*np.sin(theta) #Ottieni accelerazione    theta_velocità += intervallo_temporale*accelerazione_angolare #Aggiorna velocità con accelerazione    theta += intervallo_temporale*theta_velocità #Aggiorna angolo con velocità angolare    return theta, theta_velocitàg = 9.8 #m/s^2l = 1.0 #mtheta = [np.radians(90)] #theta_0theta_velocità = 0 #Inizia con velocità 0intervallo_temporale = 20/300 #Definisci un intervallo di tempotempo_span = np.linspace(0,20,300) #simula per 20s suddivisi in 300 intervalli di tempoper t in tempo_span:    theta_nuovo, theta_velocità = pendolo_completo(g,l,theta[-1], theta_velocità, intervallo_temporale)    theta.append(theta_nuovo)#Converti nuovamente in coordinate cartesiane x = l*np.sin(theta)y = -l*np.cos(theta)

Abbiamo simulato un pendolo completo, ma questo è ancora un sistema ben definito. È ora il momento di entrare nel caos del doppio pendolo.

Caos e il Pendolo Doppio

Il caos, nel senso matematico, si riferisce a sistemi altamente sensibili alle loro condizioni iniziali. Anche piccoli cambiamenti nell’inizio del sistema porteranno a comportamenti molto diversi man mano che il sistema si evolve. Questo descrive perfettamente il movimento del pendolo doppio. A differenza del pendolo singolo, non è un sistema ben comportato e si evolverà in modo molto diverso anche con piccoli cambiamenti nell’angolo di partenza.

Per modellare il movimento del pendolo doppio, useremo lo stesso approccio lagrangiano come prima (vedi derivazione completa).

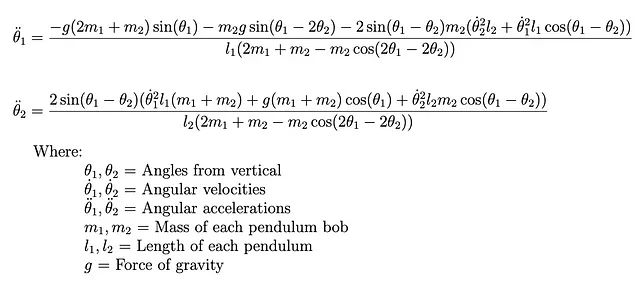
Utilizzeremo anche lo stesso schema di integrazione numerica come prima quando implementiamo questa equazione nel codice e troviamo theta.

#Get theta1 acceleration def theta1_acceleration(m1,m2,l1,l2,theta1,theta2,theta1_velocity,theta2_velocity,g):    mass1 = -g*(2*m1 + m2)*np.sin(theta1)    mass2 = -m2*g*np.sin(theta1 - 2*theta2)    interaction = -2*np.sin(theta1 - theta2)*m2*np.cos(theta2_velocity**2*l2 + theta1_velocity**2*l1*np.cos(theta1 - theta2))    normalization = l1*(2*m1 + m2 - m2*np.cos(2*theta1 - 2*theta2))        theta1_ddot = (mass1 + mass2 + interaction)/normalization        return theta1_ddot#Get theta2 accelerationdef theta2_acceleration(m1,m2,l1,l2,theta1,theta2,theta1_velocity,theta2_velocity,g):    system = 2*np.sin(theta1 - theta2)*(theta1_velocity**2*l1*(m1 + m2) + g*(m1 + m2)*np.cos(theta1) + theta2_velocity**2*l2*m2*np.cos(theta1 - theta2))    normalization = l1*(2*m1 + m2 - m2*np.cos(2*theta1 - 2*theta2))        theta2_ddot = system/normalization    return theta2_ddot#Update theta1def theta1_update(m1,m2,l1,l2,theta1,theta2,theta1_velocity,theta2_velocity,g,time_step):    #Numerical Integration    theta1_velocity += time_step*theta1_acceleration(m1,m2,l1,l2,theta1,theta2,theta1_velocity,theta2_velocity,g)    theta1 += time_step*theta1_velocity    return theta1, theta1_velocity#Update theta2def theta2_update(m1,m2,l1,l2,theta1,theta2,theta1_velocity,theta2_velocity,g,time_step):    #Numerical Integration    theta2_velocity += time_step*theta2_acceleration(m1,m2,l1,l2,theta1,theta2,theta1_velocity,theta2_velocity,g)    theta2 += time_step*theta2_velocity    return theta2, theta2_velocity#Run full double pendulumdef double_pendulum(m1,m2,l1,l2,theta1,theta2,theta1_velocity,theta2_velocity,g,time_step,time_span):    theta1_list = [theta1]    theta2_list = [theta2]        for t in time_span:        theta1, theta1_velocity = theta1_update(m1,m2,l1,l2,theta1,theta2,theta1_velocity,theta2_velocity,g,time_step)        theta2, theta2_velocity = theta2_update(m1,m2,l1,l2,theta1,theta2,theta1_velocity,theta2_velocity,g,time_step)        theta1_list.append(theta1)        theta2_list.append(theta2)        x1 = l1*np.sin(theta1_list) #Pendulum 1 x    y1 = -l1*np.cos(theta1_list) #Pendulum 1 y    x2 = l1*np.sin(theta1_list) + l2*np.sin(theta2_list) #Pendulum 2 x    y2 = -l1*np.cos(theta1_list) - l2*np.cos(theta2_list) #Pendulum 2 y        return x1,y1,x2,y2

#Definisci i parametri del sistema g = 9.8 #m/s^2m1 = 1 #kgm2 = 1 #kgl1 = 1 #ml2 = 1 #mtheta1 = np.radians(90)theta2 = np.radians(45)theta1_velocity = 0 #m/stheta2_velocity = 0 #m/stheta1_list = [theta1]theta2_list = [theta2]time_step = 20/300time_span = np.linspace(0,20,300)x1,y1,x2,y2 = double_pendulum(m1,m2,l1,l2,theta1,theta2,theta1_velocity,theta2_velocity,g,time_step,time_span)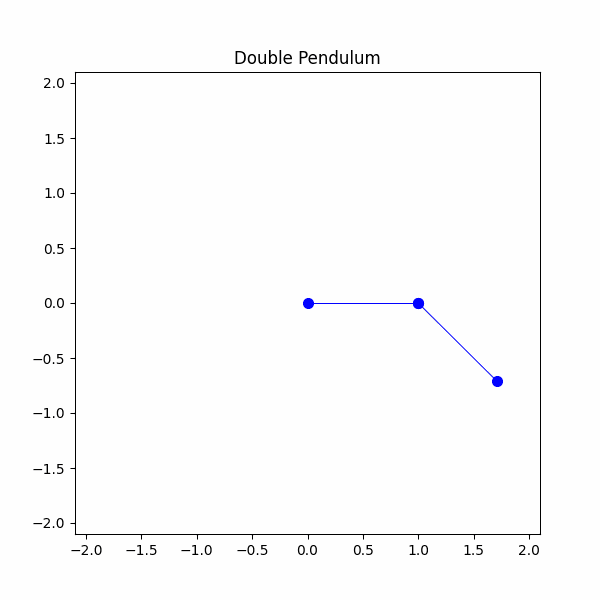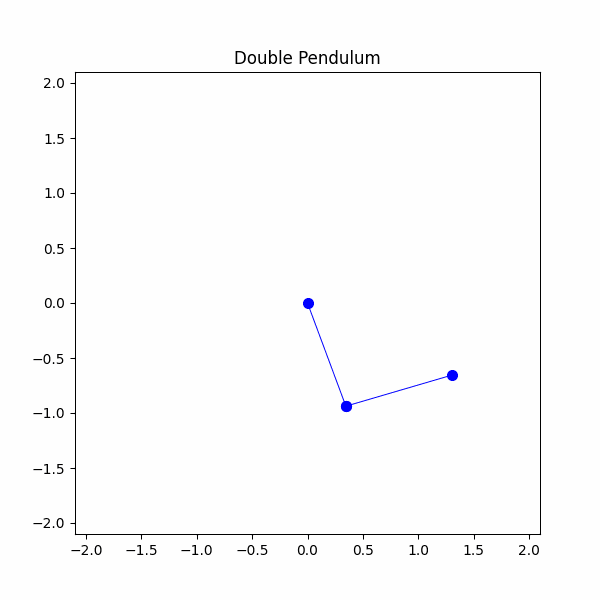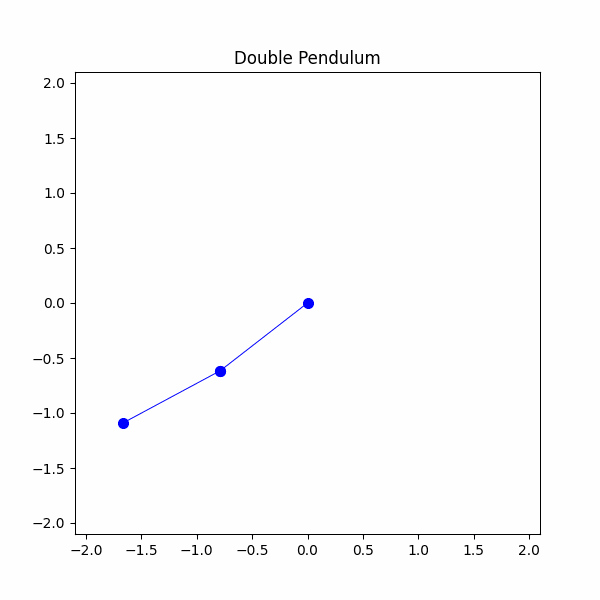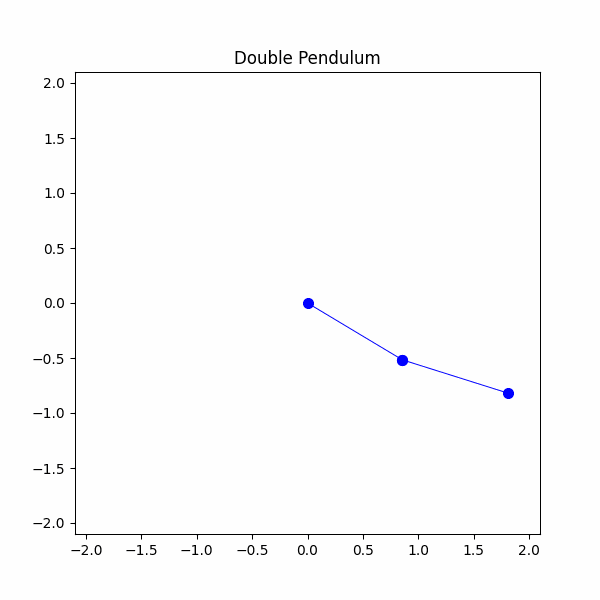

Ci siamo finalmente riusciti! Abbiamo modellato con successo un pendolo doppio, ma ora è il momento di osservare un po’ di caos. La nostra simulazione finale sarà di due pendoli doppi con condizioni iniziali leggermente diverse. Imposteremo un pendolo per avere un theta 1 di 90 gradi e l’altro per avere un theta 1 di 91 gradi. Vediamo cosa succede.

Possiamo vedere che entrambi i pendoli iniziano con traiettorie simili ma si divergono rapidamente. Questo è ciò che intendiamo quando parliamo di caos, anche una differenza di 1 grado nell’angolo si traduce in un comportamento finale molto diverso.

Conclusioni

In questo articolo abbiamo imparato il movimento del pendolo e come modellarlo. Abbiamo iniziato dal modello di moto armonico più semplice e siamo arrivati al pendolo doppio complesso e caotico. Lungo il percorso abbiamo imparato sulla Lagrangiana, il caos e l’integrazione numerica.

Il pendolo doppio è il più semplice esempio di un sistema caotico. Questi sistemi esistono ovunque nel nostro mondo, dalle dinamiche di popolazione, al clima e persino al biliardo. Possiamo applicare le lezioni apprese dal pendolo doppio ogni volta che incontriamo sistemi caotici.

Punti chiave

• I sistemi caotici sono molto sensibili alle condizioni iniziali e si evolveranno in modi molto diversi anche con piccoli cambiamenti all’inizio.
• Quando si tratta di un sistema, specialmente un sistema caotico, c’è un altro punto di riferimento da cui guardarlo che rende più facile lavorarci? (Come il riferimento di forza al riferimento di energia)
• Quando i sistemi diventano troppo complicati, dobbiamo implementare soluzioni numeriche per risolverli. Queste soluzioni sono semplici ma potenti e offrono buone approssimazioni al comportamento reale.

Riferimenti

Tutte le figure utilizzate in questo articolo sono state create dall’autore o provengono da Math Images e sono coperte dalla GNU Free Documentation License 1.2

Tutto – Sì, Tutto – È un oscillatore armonico

Gli studenti universitari di fisica potrebbero scherzare dicendo che l’universo è fatto di oscillatori armonici, ma non sono lontani dalla verità.

www.wired.com

Classical Mechanics, John Taylor https://neuroself.files.wordpress.com/2020/09/taylor-2005-classical-mechanics.pdf

Codice completo

Pendolo Semplice

def makeGif(x,y,name):    !mkdir frames        counter=0    images = []    for i in range(0,len(x)):        plt.figure(figsize = (6,6))        plt.plot([0,x[i]],[0,y[i]], "o-", color = "b", markersize = 7, linewidth=.7 )        plt.title("Pendolo")        plt.xlim(-1.1,1.1)        plt.ylim(-1.1,1.1)        plt.savefig("frames/" + str(counter)+ ".png")        images.append(imageio.imread("frames/" + str(counter)+ ".png"))        counter += 1        plt.close()    imageio.mimsave(name, images)    !rm -r framesdef simple_pendulum(theta_0, omega, t, phi):    theta = theta_0*np.cos(omega*t + phi)    return theta#parametri del nostro sistematheta_0 = np.radians(15) #gradi in radianti g = 9.8 #m/s^2l = 1.0 #momega = np.sqrt(g/l)phi = 0 #per angoli piccolitime_span = np.linspace(0,20,300) #simulazione per 20s suddivisa in 300 intervalli di tempotheta = []for t in time_span:    theta.append(simple_pendulum(theta_0, omega, t, phi))x = l*np.sin(theta)y = -l*np.cos(theta) #negativo per assicurarsi che il pendolo sia rivolto verso il basso

Pendolo

def pendolo_completo(g,l,theta,theta_velocità, step_temporale):    theta_accelerazione = -(g/l)*np.sin(theta)    theta_velocità += step_temporale*theta_accelerazione    theta += step_temporale*theta_velocità    return theta, theta_velocitàg = 9.8 #m/s^2l = 1.0 #mtheta = [np.radians(90)] #theta_0theta_velocità = 0step_temporale = 20/300intervallo_temporale = np.linspace(0,20,300) #simula per 20s diviso in 300 intervalli temporalifor t in intervallo_temporale:    theta_nuovo, theta_velocità = pendolo_completo(g,l,theta[-1], theta_velocità, step_temporale)    theta.append(theta_nuovo)#Converti di nuovo in coordinate cartesiane x = l*np.sin(theta)y = -l*np.cos(theta)#Usa la stessa funzione del pendolo semplice creaGif(x,y,"pendolo.gif")

Doppio Pendolo

def accelerazione_theta1(m1,m2,l1,l2,theta1,theta2,theta1_velocità,theta2_velocità,g):    massa1 = -g*(2*m1 + m2)*np.sin(theta1)    massa2 = -m2*g*np.sin(theta1 - 2*theta2)    interazione = -2*np.sin(theta1 - theta2)*m2*np.cos(theta2_velocità**2*l2 + theta1_velocità**2*l1*np.cos(theta1 - theta2))    normalizzazione = l1*(2*m1 + m2 - m2*np.cos(2*theta1 - 2*theta2))        theta1_ddot = (massa1 + massa2 + interazione)/normalizzazione        return theta1_ddotdef accelerazione_theta2(m1,m2,l1,l2,theta1,theta2,theta1_velocità,theta2_velocità,g):    sistema = 2*np.sin(theta1 - theta2)*(theta1_velocità**2*l1*(m1 + m2) + g*(m1 + m2)*np.cos(theta1) + theta2_velocità**2*l2*m2*np.cos(theta1 - theta2))    normalizzazione = l1*(2*m1 + m2 - m2*np.cos(2*theta1 - 2*theta2))        theta2_ddot = sistema/normalizzazione    return theta2_ddotdef aggiorna_theta1(m1,m2,l1,l2,theta1,theta2,theta1_velocità,theta2_velocità,g,step_temporale):        theta1_velocità += step_temporale*accelerazione_theta1(m1,m2,l1,l2,theta1,theta2,theta1_velocità,theta2_velocità,g)    theta1 += step_temporale*theta1_velocità    return theta1, theta1_velocitàdef aggiorna_theta2(m1,m2,l1,l2,theta1,theta2,theta1_velocità,theta2_velocità,g,step_temporale):        theta2_velocità += step_temporale*accelerazione_theta2(m1,m2,l1,l2,theta1,theta2,theta1_velocità,theta2_velocità,g)    theta2 += step_temporale*theta2_velocità    return theta2, theta2_velocitàdef doppio_pendolo(m1,m2,l1,l2,theta1,theta2,theta1_velocità,theta2_velocità,g,step_temporale,intervallo_temporale):    lista_theta1 = [theta1]    lista_theta2 = [theta2]        for t in intervallo_temporale:        theta1, theta1_velocità = aggiorna_theta1(m1,m2,l1,l2,theta1,theta2,theta1_velocità,theta2_velocità,g,step_temporale)        theta2, theta2_velocità = aggiorna_theta2(m1,m2,l1,l2,theta1,theta2,theta1_velocità,theta2_velocità,g,step_temporale)        lista_theta1.append(theta1)        lista_theta2.append(theta2)        x1 = l1*np.sin(lista_theta1)    y1 = -l1*np.cos(lista_theta1)    x2 = l1*np.sin(lista_theta1) + l2*np.sin(lista_theta2)    y2 = -l1*np.cos(lista_theta1) - l2*np.cos(lista_theta2)        return x1,y1,x2,y2

#Definisci i parametri del sistema, esegui il doppio pendolog = 9.8 #m/s^2m1 = 1 #kgm2 = 1 #kgl1 = 1 #ml2 = 1 #mtheta1 = np.radians(90)theta2 = np.radians(45)theta1_velocità = 0 #m/stheta2_velocità = 0 #m/stheta1_list = [theta1]theta2_list = [theta2]step_temporale = 20/300intervallo_temporale = np.linspace(0,20,300)for t in intervallo_temporale:    theta1, theta1_velocità = aggiorna_theta1(m1,m2,l1,l2,theta1,theta2,theta1_velocità,theta2_velocità,g,step_temporale)    theta2, theta2_velocità = aggiorna_theta2(m1,m2,l1,l2,theta1,theta2,theta1_velocità,theta2_velocità,g,step_temporale)        theta1_list.append(theta1)    theta2_list.append(theta2)    x1 = l1*np.sin(theta1_list)y1 = -l1*np.cos(theta1_list)x2 = l1*np.sin(theta1_list) + l2*np.sin(theta2_list)y2 = -l1*np.cos(theta1_list) - l2*np.cos(theta2_list)

#Crea Gif!mkdir frames    counter=0immagini = []for i in range(0,len(x1)):    plt.figure(figsize = (6,6))    plt.figure(figsize = (6,6))    plt.plot([0,x1[i]],[0,y1[i]], "o-", color = "b", markersize = 7, linewidth=.7 )    plt.plot([x1[i],x2[i]],[y1[i],y2[i]], "o-", color = "b", markersize = 7, linewidth=.7 )    plt.title("Doppio Pendolo")    plt.xlim(-2.1,2.1)    plt.ylim(-2.1,2.1)    plt.savefig("frames/" + str(counter)+ ".png")    immagini.append(imageio.imread("frames/" + str(counter)+ ".png"))    counter += 1    plt.close()imageio.mimsave("doppio_pendolo.gif", immagini)!rm -r frames