Ricerca di similarità, Parte 6 Proiezioni casuali con LSH Forest
LSH Forest Random Projections for Similarity Search, Part 6
Comprendere come hashare i dati e rifletterne la similarità attraverso la costruzione di iperpiani casuali

La ricerca di similarità è un problema in cui, dato un query, l’obiettivo è trovare i documenti più simili ad esso tra tutti i documenti del database.
Introduzione
Nella scienza dei dati, la ricerca di similarità appare spesso nel dominio del NLP, nei motori di ricerca o nei sistemi di raccomandazione dove è necessario recuperare i documenti o gli elementi più rilevanti per una query. Esistono molteplici modi per migliorare le prestazioni di ricerca in volumi massivi di dati.
Nella parte precedente, abbiamo esaminato il principale paradigma di LSH che consiste nel trasformare i vettori di input in valori hash di dimensioni inferiori, preservando al contempo le informazioni sulla loro similarità. Per ottenere i valori hash (firme) sono state utilizzate le funzioni minhash. In questo articolo, proietteremo casualmente i dati di input per ottenere vettori binari analoghi.
- Frequentista vs Statistica Bayesiana in Data Science
- Ricercatori del CMU propongono GILL un metodo di intelligenza artificiale per fondere LLM con modelli di codifica e decodifica delle immagini.
- Incontra MultiDiffusion Un framework AI unificato che consente la generazione di immagini versatile e controllabile utilizzando un modello di diffusione testo-immagine pre-addestrato.
Ricerca di similarità, Parte 5: Locality Sensitive Hashing (LSH)
Esplora come le informazioni sulla similarità possono essere incorporate nella funzione di hash
towardsdatascience.com
Idea
Considera un gruppo di punti in uno spazio ad alta dimensione. È possibile costruire un iperpiano casuale che funge da parete e separa ciascun punto in due sottogruppi: positivo e negativo. Ad ogni punto sul lato positivo viene assegnato il valore “1” e ad ogni punto sul lato negativo viene assegnato il valore “0”.
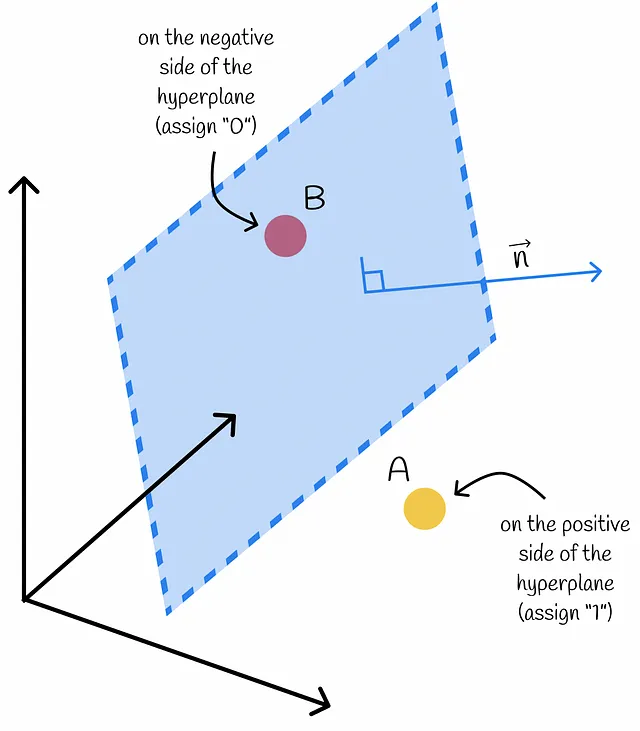
Come si può determinare il lato di un iperpiano per un certo vettore? Utilizzando il prodotto interno! Tornando all’essenza dell’algebra lineare, il segno del prodotto scalare tra un vettore dato e il vettore normale all’iperpiano determina su quale lato si trova il vettore. In questo modo, ogni vettore del dataset può essere separato in uno dei due lati.
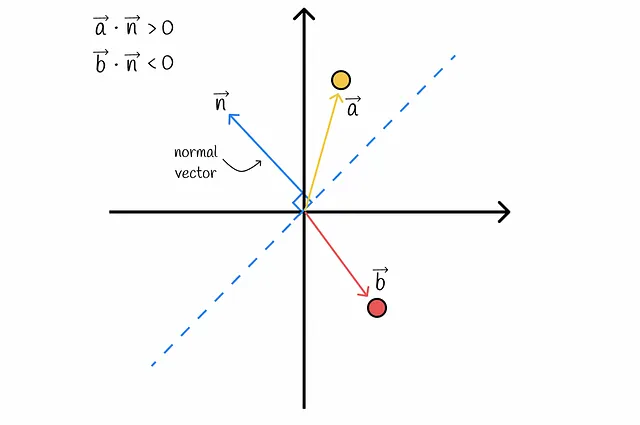
Ovviamente, codificare ogni vettore del dataset con un singolo valore binario non è sufficiente. Dovrebbero essere costruiti diversi iperpiani casuali, in modo che ogni vettore possa essere codificato con tanti valori di 0 e 1 in base alla sua posizione relativa a un iperpiano specifico. Se due vettori hanno lo stesso codice binario, ciò indica che nessuno degli iperpiani costruiti potrebbe averli separati in regioni diverse. Pertanto, è probabile che siano molto vicini l’uno all’altro nella realtà.
Per trovare il vicino più vicino per una determinata query, è sufficiente codificare la query con 0 e 1 nello stesso modo, controllando la sua posizione relativa a tutti gli iperpiani. Il vettore binario trovato per la query può essere confrontato con tutti gli altri vettori binari ottenuti per i vettori del dataset. Questo può essere fatto linearmente utilizzando la distanza di Hamming.
La distanza di Hamming tra due vettori è il numero di posizioni in cui i loro valori sono diversi.

I vettori binari con le distanze di Hamming più basse rispetto alla query vengono presi come candidati e quindi confrontati completamente con la query iniziale.
Perché gli iperpiani vengono costruiti casualmente?
Nella fase attuale, sembra logico chiedersi perché gli iperpiani vengono costruiti in modo casuale e non in modo deterministico, cioè potrebbero essere definite regole personalizzate per separare i punti del dataset. Ci sono due motivi principali dietro a questo:
- Innanzitutto, l’approccio deterministico non è in grado di generalizzare l’algoritmo e può portare all’overfitting.
- In secondo luogo, la casualità consente di formulare affermazioni probabilistiche sulle prestazioni dell’algoritmo che non dipendono dai dati di input. Per un approccio deterministico, ciò non funzionerebbe perché potrebbe funzionare bene su alcuni dati e avere una scarsa prestazione su altri. Un buon esempio di ciò è l’algoritmo di quick-sort deterministico che funziona in media in tempo O(n * log n). Tuttavia, funziona in tempo O(n²) su un array ordinato come scenario peggiore. Se qualcuno ha conoscenza del flusso di lavoro dell’algoritmo, queste informazioni possono essere utilizzate per danneggiare in modo significativo l’efficienza del sistema fornendo sempre i dati peggiori. Ecco perché è molto più preferibile un quick-sort casuale. La stessa situazione si verifica con gli iperpiani casuali.
Perché le proiezioni casuali LSH vengono chiamate anche “alberi”?
Il metodo delle proiezioni casuali viene talvolta chiamato LSH Tree. Questo perché il processo di assegnazione del codice hash può essere rappresentato sotto forma di un albero decisionale in cui ogni nodo contiene una condizione che indica se un vettore si trova sul lato negativo o positivo di un iperpiano corrente.
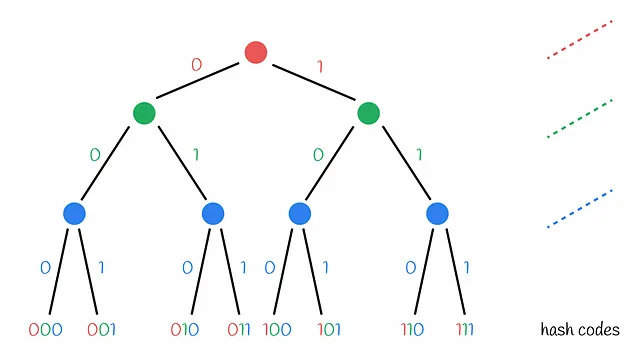
Foresta di iperpiani
Gli iperpiani vengono costruiti in modo casuale. Questo può comportare una situazione in cui separano male i punti del dataset, come mostrato nella figura sottostante.

Tecnicamente, non è un grosso problema quando due punti hanno lo stesso codice hash ma sono lontani l’uno dall’altro. Nel passaggio successivo dell’algoritmo, questi punti vengono presi come candidati e confrontati completamente, in questo modo l’algoritmo può eliminare i casi di falsi positivi. La situazione è più complicata con i falsi negativi: quando due punti hanno diversi codici hash ma in realtà sono vicini l’uno all’altro.
Perché non utilizzare lo stesso approccio con gli alberi decisionali dell’apprendimento automatico classico che vengono combinati in foreste casuali per migliorare la qualità complessiva delle previsioni? Se un stimatore commette un errore, gli altri stimatori possono produrre previsioni migliori e ridurre l’errore di previsione finale. Utilizzando questa idea, il processo di costruzione di iperpiani casuali può essere ripetuto in modo indipendente. I valori hash risultanti possono essere aggregati per una coppia di vettori in modo simile a quanto fatto con i valori minhash nel capitolo precedente:
Se una query ha lo stesso codice hash almeno una volta con un altro vettore, allora vengono considerati candidati.
Utilizzando questo meccanismo è possibile ridurre il numero di falsi negativi.
Trade-off tra qualità e velocità
È importante scegliere un numero appropriato di iperpiani da eseguire sul dataset. Più iperpiani vengono scelti per suddividere i punti del dataset, meno collisioni ci sono e più tempo ci vuole per calcolare i codici hash e più memoria per memorizzarli. In parole precise, se un dataset è composto da n vettori e lo dividiamo in k iperpiani, allora in media ogni possibile codice hash verrà assegnato a n / 2ᵏ vettori.
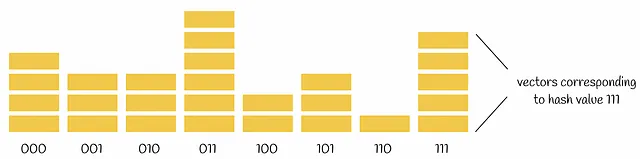
Complessità
Allenamento
La fase di allenamento di LSH Forest consiste in due parti:
- Generazione di k iperpiani. Questa è una procedura relativamente veloce poiché un singolo iperpiano in uno spazio d-dimensionale può essere generato in O(d) di tempo.
- Assegnazione dei codici hash a tutti i vettori del dataset. Questo passaggio potrebbe richiedere tempo, soprattutto per dataset di grandi dimensioni. Ottenere un singolo codice hash richiede O(dk) di tempo. Se un dataset è composto da n vettori, la complessità totale diventa O(ndk).
Il processo sopra descritto viene ripetuto diverse volte per ogni albero nella foresta.
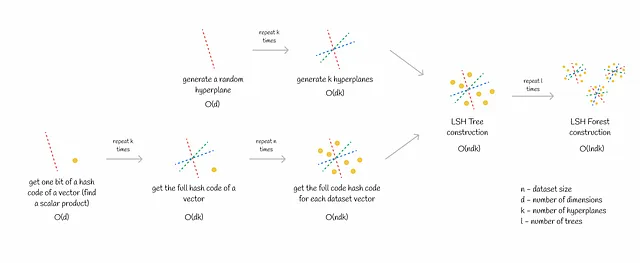
Inferenza
Uno dei vantaggi di LSH Forest è la sua inferenza veloce che include due passaggi:
- Ottenere il codice hash di una query. Questo è equivalente al calcolo di k prodotti scalari che richiedono O(dk) di tempo (d – dimensionalità).
- Trovare i vicini più vicini alla query nello stesso bucket (vettori con lo stesso codice hash) calcolando distanze precise ai candidati. Il calcolo della distanza procede linearmente per O(d). Ogni bucket contiene in media n / 2ᵏ vettori. Pertanto, il calcolo della distanza per tutti i potenziali candidati richiede O(dn / 2ᵏ) di tempo.
La complessità totale è O(dk + dn / 2ᵏ).
Come al solito, il processo sopra descritto viene ripetuto diverse volte per ogni albero nella foresta.
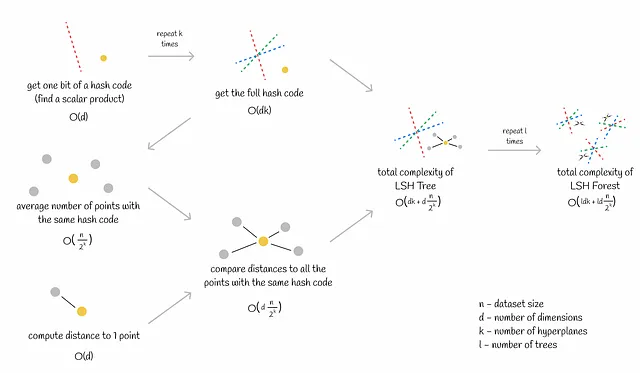
Quando il numero di iperpiani k è scelto in modo tale che n ~ 2ᵏ (cosa possibile nella maggior parte dei casi), la complessità totale dell’inferenza diventa O(ldk) (l è il numero di alberi). Fondamentalmente, questo significa che il tempo di calcolo non dipende dalle dimensioni del dataset! Questa sottigliezza porta a una scalabilità efficiente della ricerca di similarità per milioni o addirittura miliardi di vettori.
Tasso di errore
Nella parte precedente dell’articolo su LSH, abbiamo discusso come trovare la probabilità che due vettori vengano scelti come candidati in base alla similarità delle loro firme. Qui useremo quasi la stessa logica per trovare la formula per LSH Forest.
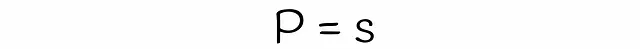

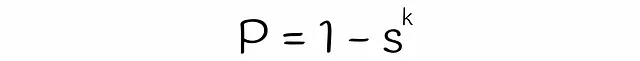
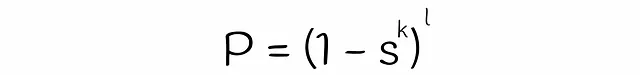
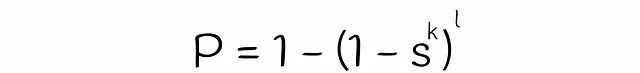
Fino ad ora abbiamo quasi ottenuto la formula per stimare la probabilità che due vettori siano candidati. L’unica cosa che manca è stimare il valore della variabile s nell’equazione. Nell’algoritmo classico LSH, s è uguale all’indice di Jaccard o alla similarità delle firme di due vettori. D’altra parte, per stimare s per LSH forest, verrà utilizzata la teoria dell’algebra lineare.
Francamente parlando, s è la probabilità che due vettori a e b abbiano lo stesso bit. Questa probabilità è equivalente alla probabilità che un iperpiano casuale separi questi vettori dallo stesso lato. Visualizziamolo:
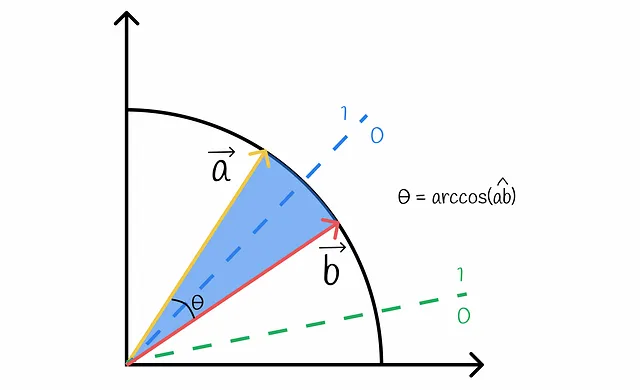
Dalla figura, è chiaro che un iperpiano separa i vettori a e b in due lati diversi solo nel caso in cui passi tra di loro. Tale probabilità q è proporzionale all’angolo tra i vettori che può essere facilmente calcolato:
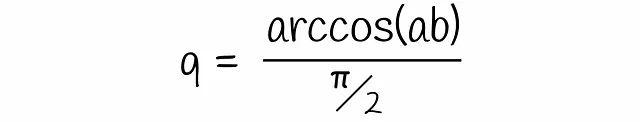
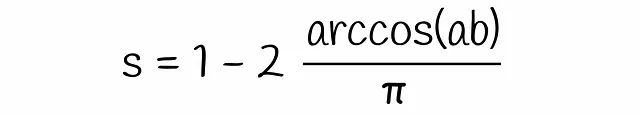
Inserendo questa equazione in quella ottenuta in precedenza si arriva alla formula finale:

Visualizzazione
Con l’ultima formula ottenuta, visualizziamo la probabilità che due vettori siano candidati in base alla loro similarità del coseno per un diverso numero di iperpiani k e alberi l.

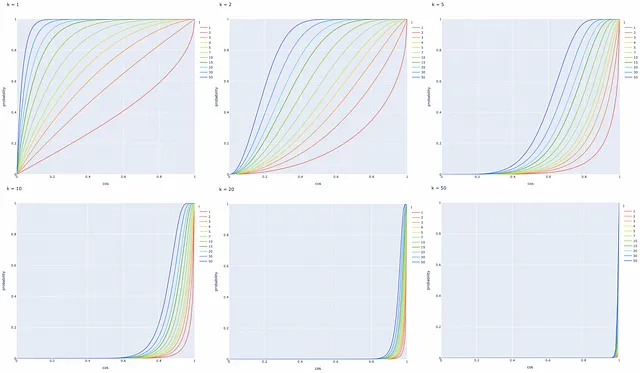
Possiamo fare diverse osservazioni utili, basate sui grafici:
- Una coppia di vettori con una similarità cosinale di 1 diventa sempre candidata.
- Una coppia di vettori con una similarità cosinale di 0 non diventa mai candidata.
- La probabilità P che due vettori siano candidati aumenta (cioè più falsi positivi) quando il numero di iperpiani k diminuisce o il numero di alberi LSH l aumenta. La dichiarazione inversa è vera.
Per riassumere, LSH è un algoritmo molto flessibile: è possibile regolare i diversi valori k e l in base a un problema specifico e ottenere la curva di probabilità che soddisfi i requisiti del problema.
Esempio
Guardiamo l’esempio seguente. Immaginiamo che siano costruiti 5 alberi con l = 5 e k = 10 iperpiani. Oltre a ciò, ci sono due vettori con una similarità cosinale del 0.8. Nella maggior parte dei sistemi, una simile similarità cosinale indica che i vettori sono molto simili tra loro. Sulla base dei risultati delle sezioni precedenti, si scopre che questa probabilità è solo del 2.5%! Ovviamente, è un risultato molto basso per una similarità cosinale così alta. Utilizzando questi parametri di l = 5 e k = 10 si ottiene un elevato numero di falsi negativi! La linea verde qui sotto rappresenta la probabilità in questo caso.
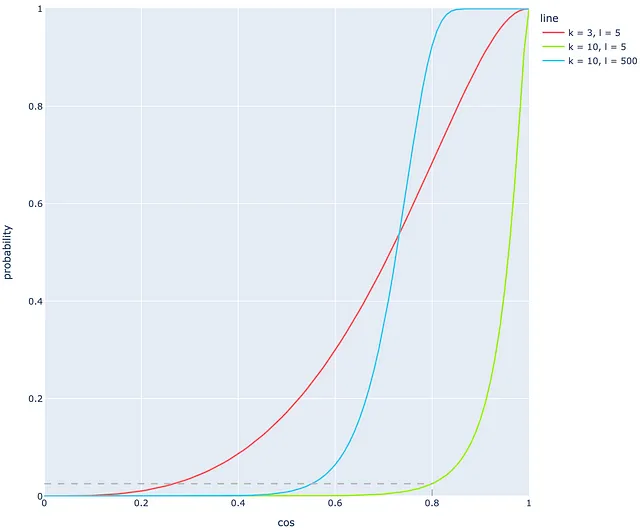
Questo problema può essere risolto regolando valori migliori per k e l per spostare la curva verso sinistra.
Ad esempio, se k viene ridotto a 3 (linea rossa), lo stesso valore di similarità cosinale del 0.8 corrisponderà a una probabilità del 68%, che è migliore rispetto prima. A prima vista, sembra che la linea rossa si adatti molto meglio alla situazione rispetto a quella verde, ma è importante tenere presente che l’utilizzo di valori piccoli di k (come nel caso della linea rossa) porta a un elevato numero di collisioni. Per questo motivo, a volte è preferibile regolare il secondo parametro, ovvero il numero di alberi l.
A differenza di k, di solito è necessario un numero molto elevato di alberi l per ottenere una forma di linea simile. Nella figura, la linea blu viene ottenuta dalla linea verde cambiando il valore di l da 10 a 500. La linea blu si adatta chiaramente meglio rispetto a quella verde, ma è ancora lontana dall’essere perfetta: a causa di una forte pendenza tra i valori di similarità cosinale di 0.6 e 0.8, la probabilità è quasi uguale a 0 per cosine di 0.3-0.5, il che è sfavorevole. Questa piccola probabilità per una similarità di documenti di 0.3-0.5 dovrebbe essere normalmente più alta nella vita reale.
Sulla base dell’ultimo esempio, è evidente che anche un numero molto elevato di alberi (che richiede molti calcoli) porta comunque a molti falsi negativi! Questo è il principale svantaggio del metodo delle proiezioni casuali:
Anche se potrebbe essere possibile ottenere una curva di probabilità perfetta, ciò richiederebbe molti calcoli o comporterebbe molti collisioni. In caso contrario, si ottiene un alto tasso di falsi negativi.
Implementazione di Faiss
Faiss (Facebook AI Search Similarity) è una libreria Python scritta in C++ utilizzata per la ricerca ottimizzata di similarità. Questa libreria presenta diversi tipi di indici, che sono strutture dati utilizzate per memorizzare ed eseguire query in modo efficiente.
Sulla base delle informazioni presenti nella documentazione di Faiss, scopriremo come costruire un indice LSH.
L’algoritmo delle proiezioni casuali è implementato in Faiss all’interno della classe IndexLSH. Anche se gli autori di Faiss utilizzano una tecnica leggermente diversa chiamata “rotazioni casuali”, essa presenta comunque somiglianze con quanto descritto in questo articolo. La classe implementa solo un singolo albero LSH. Se vogliamo utilizzare una foresta LSH, è sufficiente creare diversi alberi LSH e aggregare i loro risultati.
Il costruttore della classe IndexLSH richiede due argomenti:
- d: il numero di dimensioni
- nbits: il numero di bit necessari per codificare un singolo vettore (il numero di bucket possibili è pari a 2ⁿᵇᶦᵗˢ)
Le distanze restituite dal metodo search() sono distanze di Hamming rispetto al vettore di query.
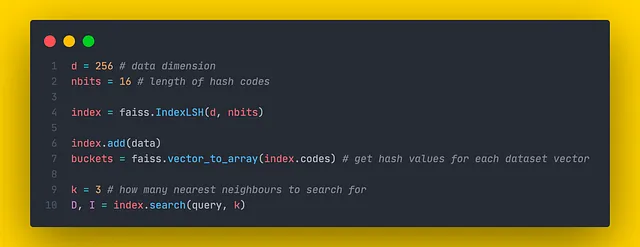
Inoltre, Faiss consente di ispezionare i valori hash codificati per ogni vettore del dataset chiamando il metodo faiss.vector_to_array(index.codes).
Dato che ogni vettore del dataset è codificato da nbits valori binari, il numero di byte necessari per memorizzare un singolo vettore è uguale a:

Lemma di Johnson-Lindenstrauss
Il lemma di Johnson-Lindenstrauss è un favoloso lemma relativo alla riduzione della dimensionalità. Sebbene possa essere difficile comprendere appieno la sua formulazione originale, può essere formulato in parole semplici:
Scegliendo un sottoinsieme casuale e proiettando i dati originali su di esso, si preservano le distanze reciproche corrispondenti tra i punti.
Per essere più precisi, avendo un dataset di n punti, è possibile rappresentarli in uno spazio di O(logn) dimensioni in modo tale che le distanze relative tra i punti saranno quasi preservate. Se un vettore è codificato da ~logn valori binari nel metodo LSH, allora il lemma può essere applicato. Inoltre, LSH crea iperpiani in modo casuale proprio come richiesto dal lemma.
Ciò che è anche incredibile del lemma di Johnson-Lindenstrauss è il fatto che il numero di dimensioni di un nuovo dataset non dipende dalla dimensionalità del dataset originale! In pratica, questo lemma non funziona bene per dimensioni molto piccole.
Conclusioni
Abbiamo esaminato un potente algoritmo per la ricerca di similarità. Basato su un’idea semplice di separare i punti tramite iperpiani casuali, di solito si comporta e scala molto bene su grandi dataset. Inoltre, offre una buona flessibilità consentendo di scegliere un numero appropriato di iperpiani e alberi.
I risultati teorici del lemma di Johnson-Lindenstrauss rafforzano l’uso dell’approccio delle proiezioni casuali.
Risorse
- LSH Forest: Indici di auto-ottimizzazione per la ricerca di similarità
- Il lemma di Johnson-Lindenstrauss
- Documentazione di Faiss
- Repository di Faiss
- Riepilogo degli indici di Faiss
Tutte le immagini, se non diversamente specificato, sono dell’autore.





