Informazione ed Entropia

Info ed Entropia

Cosa, Perché e Come spiegato

Usa l’entropia e non potrai mai perdere un dibattito, disse von Neumann a Shannon perché nessuno sa davvero cosa sia l’entropia.

— William Poundstone

Iniziamo con un po’ di storia.

Nel 1948, un matematico di nome Claude E. Shannon pubblicò un articolo intitolato “Una teoria matematica della comunicazione”, che introdusse un concetto fondamentale nell’Apprendimento Automatico: l’entropia.

• Mappare gli ingorghi Analisi del traffico utilizzando la teoria dei grafi
• Nuovo modello di testo-immagine di Metas – Spiegazione del paper CM3leon
• Il Chief Scientist di NVIDIA, Bill Dally, terrà il discorso principale a Hot Chips

Mentre l’entropia misura il disordine in fisica, il suo significato cambia nella teoria dell’informazione. Tuttavia, entrambi misurano il disordine o l’incertezza.

Approfondiamo la nozione di “Informazione”.

I. Informazione di Shannon

Secondo l’articolo, possiamo quantificare l’informazione che un evento trasmette, che può essere interpretata come la misura del “sorprendente”. Significa che il contenuto informativo rappresenta essenzialmente l’entità della sorpresa contenuta in un evento.

Prendiamo un esempio: Immagina che qualcuno ti dica: “Gli animali hanno bisogno di acqua per sopravvivere”. Quanto saresti sorpreso nel sentire questa frase?

Non saresti sorpreso affatto perché è un fatto ben noto e costantemente vero. In questo scenario, la quantità di sorpresa equivale a 0 e di conseguenza, l’informazione trasmessa sarebbe anche 0.

Ma cosa succederebbe se qualcuno dicesse: “Ho ottenuto croce lanciando una moneta”? Beh, questo evento (ottenere croce) non è garantito, vero? C’è sempre una possibilità del 50-50 che l’esito possa essere testa o croce. Di conseguenza, sentire questa affermazione potrebbe suscitare un certo livello di sorpresa. Qui sta una correlazione affascinante tra probabilità e sorpresa. Quando un evento è assolutamente certo (con una probabilità di 1), la misura della sorpresa diminuisce (diventa 0). Al contrario, man mano che la probabilità diminuisce, ovvero l’evento diventa meno probabile, il senso di sorpresa aumenta. Questa è la relazione inversa tra probabilità e sorpresa.

Matematicamente,

dove p(x) è la probabilità di un evento x.

Sappiamo che l’informazione non è altro che una quantità di sorpresa. E poiché stiamo cercando di fare un po’ di matematica qui, possiamo sostituire la parola “sorprendente” con “informazione”.

Cosa succederebbe se facessi informazione = 1/p(x)?

Esaminiamo questo in alcuni casi limite:

Quando p(x) = 0, informazione = 1/0 = ∞ (infinito/non definito). Questo risultato si allinea con la nostra intuizione: un evento che era considerato impossibile ma è comunque accaduto produrrebbe sorpresa/informazione infinita o non definita. (Uno scenario impossibile) ➟ ✅

Quando p(x)=1, informazione = 1/1 = 1, il che contraddice la nostra osservazione. Idealmente, puntiamo a 0 sorprese nel caso di un evento assolutamente probabile.

➟ ❌

Fortunatamente, la funzione logaritmica è utile. (In tutto questo post, useremo costantemente il log₂ indicato come log.)

Informazione = log ( 1/p(x) ) = log(1) — log( p(x) ) = 0 — log( p(x) )

Informazione = -log( p(x) )

Esaminiamo questa nuova equazione in alcuni casi limite:

quando p(x) = 0 , informazione = -log( 0 )= ∞ ➟ ✅

quando p(x) = 1, informazione = -log(1) = 0, che è effettivamente l’outcome desiderato poiché un evento assolutamente probabile non dovrebbe comportare sorpresa/informazione ➟ ✅

Quindi, per misurare la quantità di sorpresa o informazione trasmessa da un evento, possiamo utilizzare la formula:

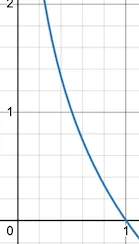
Questa funzione -log restituisce 0 quando x = 1 (il che significa che quando la probabilità è 1, l’informazione è 0). Man mano che x diminuisce, il valore corrispondente di y aumenta rapidamente. Quando x = 0, l’informazione diventa infinita o non definita. Questa curva cattura accuratamente la nostra comprensione intuitiva dell’informazione.

E per una serie di eventi, diventa

Che non è altro che la somma delle informazioni su ciascun evento. L’unità di informazione è ‘bits’. Ecco un altro punto di vista intuitivo:

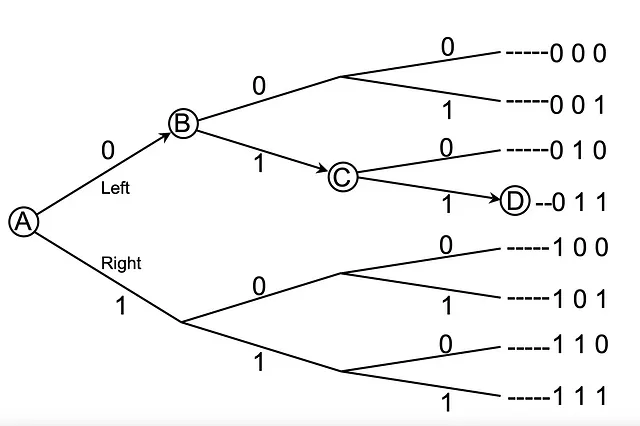
Immagina di essere al punto A e di voler raggiungere il punto D. Tuttavia, non hai idea dei percorsi e non hai visibilità dei punti adiacenti. Inoltre, non puoi tornare indietro.

Mentre sei ad A, hai due scelte Sinistra(0) e Destra(1). Ti invio un singolo bit, 0, un bit di informazione che ti aiuta a scegliere tra 2 opzioni (seconda colonna). Al tuo arrivo a B, ti fornisco un valore di bit pari a 1, per un totale di 2 bit, che ti permette di scegliere tra 2 * 2 = 4 opzioni (terza colonna). Quando ti sposti verso C, ti invio un altro 1, per un totale di 3 bit. Questo ti aiuta a scegliere tra 2 * 2 * 2 = 8 opzioni (ultima colonna). E interessante notare che 1 è il logaritmo di 2, 2 è il logaritmo di 4 e 3 è il logaritmo di 8.

‘n’ bit di informazione ci permettono di scegliere tra ‘m’ opzioni.

Ad esempio, 8 = 2 ³ (dove m = 8 rappresenta gli esiti possibili totali e n = 3 rappresenta il numero di bit)

In generale,

m = 2ⁿ

Questa è l’equazione per l’informazione (numero di bit utili).

L’intuizione di base dietro la teoria dell’informazione è che apprendere che si è verificato un evento improbabile è più informativo che apprendere che si è verificato un evento probabile.

— Pagina 73, Deep Learning, 2016.

II. Entropia

Consideriamo uno scenario in cui vogliamo generare numeri casuali da una lista data [1, 2, 3, 4] utilizzando la distribuzione di probabilità.

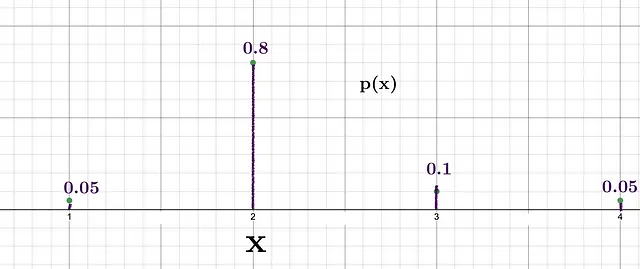
Possiamo vedere che la probabilità di ottenere 2 è la più alta, il che significa che il livello di sorpresa nel caso in cui si ottenga 2 sarebbe relativamente inferiore rispetto alla sorpresa nel caso in cui si ottenga 3, che ha una probabilità di 0.1. Le informazioni di Shannon per questi due eventi sono:

• Informazione per 2 = -log(0.8) = 0.32 bits
• Informazione per 3 = -log(0.1) = 3.32 bits

Notare che ogni volta che generiamo un numero, le informazioni ottenute variano.

Supponiamo di effettuare questo processo di generazione 100 volte seguendo la distribuzione fornita. Per calcolare le informazioni totali, dobbiamo sommare le informazioni individuali ottenute in ogni istanza.

Numero di osservazioni che generano 1 = 0,05 * 100 = 5,

Numero di osservazioni che generano 2 = 0,8 * 100 = 80

Numero di osservazioni che generano 3 = 0,1 * 100 = 10

Numero di osservazioni che generano 4 = 0,05 * 100 = 5

Ora calcoliamo le informazioni totali fornite dalle 100 generazioni.

Informazioni ottenute generando 1 per 5 volte = — log(0,05) * 5 = 21,6 bit

Informazioni ottenute generando 2 per 80 volte = — log(0,8) * 80 = 25,8 bit

Informazioni ottenute generando 3 per 10 volte = — log(0,1) * 10 = 23,2 bit

Informazioni ottenute generando 4 per 5 volte = — log(0,05) * 5 = 21,6 bit

Informazioni totali = 92,2 bit

Quindi, le informazioni totali fornite dalle 100 osservazioni sono 92,2 bit.

Non sarebbe bello se calcolassimo le informazioni per osservazione (in media)?

Informazione media della distribuzione sopra = 92,2 / 100 (perché abbiamo avuto 100 osservazioni)

Informazione media = 0,922 bit

YESSS, questa è la quantità che chiamiamo ENTROPIA.

Niente di straordinario qui, è solo una quantità media (prevista) di informazioni fornite da una distribuzione di probabilità. Ora deriviamo una formula per l’Entropia.

p(x) × N dà il numero di occorrenze dell’evento x quando vengono effettuate N osservazioni totali.

Quindi, l’equazione generale finale è

Dove H è l’entropia, ed E è l’aspettativa.

Potete seguirmi mentre continuerò a scrivere su IA e Matematica.

Riferimenti

[1] C. E. SHANNON, “A Mathematical Theory of Communication”, 1948

[2] Josh Stramer, “Entropy (for data science) Clearly Explained!!!”, Youtube, 2022

[3] James V Stone, “Information Theory: A Tutorial Introduction”, 2018