Una guida per principianti per comprendere le prestazioni dei test A/B attraverso simulazioni Monte Carlo

Guida per principianti sulle prestazioni dei test A/B tramite simulazioni Monte Carlo

Questo tutorial esplora come le covariate influenzano la precisione del test A/B in un esperimento randomizzato. Un test A/B correttamente randomizzato calcola il miglioramento confrontando il risultato medio nei gruppi di trattamento e di controllo. Tuttavia, l’influenza delle caratteristiche diverse dal trattamento sul risultato determina le proprietà statistiche del test A/B. Ad esempio, l’omissione delle caratteristiche influenti nel calcolo del miglioramento del test può portare a una stima molto imprecisa del miglioramento, anche se converge al valore reale all’aumentare della dimensione del campione.

Imparerai cosa sono RMSE, bias e dimensione di un test e comprenderai le performance di un test A/B attraverso la generazione di dati simulati e l’esecuzione di esperimenti Monte Carlo. Questo tipo di lavoro è utile per capire come le proprietà del Processo di Generazione dei Dati (DGP) influenzino le performance del test A/B e ti aiuterà a portare questa comprensione nell’esecuzione di test A/B su dati del mondo reale. Prima di tutto, discutiamo alcune proprietà statistiche di un estimatore.

Proprietà statistiche di un estimatore

Errore quadratico medio (RMSE)

RMSE (Root Mean Square Error): RMSE è una misura frequentemente utilizzata delle differenze tra i valori previsti da un modello o un estimatore e i valori osservati. È la radice quadrata delle medie delle differenze quadrate tra la previsione e l’osservazione effettiva. La formula per il RMSE è:

RMSE = sqrt[(1/n) * Σ(osservato – previsione)²]

• Crea il tuo assistente di analisi dati con gli agenti di Langchain
• Può l’IA davvero aiutarti a superare i colloqui?
• Knowledge Graph Il Cambiamento di Gioco in AI e Data Science

Il RMSE attribuisce un peso relativamente alto agli errori grandi perché vengono elevati al quadrato prima di essere mediati, il che significa che il RMSE dovrebbe essere più utile quando gli errori grandi sono indesiderabili.

Bias

In statistica, il bias di un estimatore è la differenza tra il valore atteso di questo estimatore e il vero valore del parametro stimato. Un estimatore o una regola di decisione con bias zero viene chiamato non distorto; altrimenti, si dice che l’estimatore è distorto. In altre parole, si ha un bias quando un algoritmo impara in modo coerente la stessa cosa errata, non riuscendo a vedere la corretta relazione sottostante.

Ad esempio, se stai cercando di prevedere i prezzi delle case in base alle caratteristiche della casa e le tue previsioni sono costantemente $100.000 al di sotto del prezzo effettivo, il tuo modello è distorto.

Dimensione

Nell’ipotesi di test nella statistica, “dimensione del test” si riferisce al livello di significatività del test, spesso indicato con la lettera greca α (alfa). Il livello di significatività, o dimensione del test, è una soglia che una statistica di test deve superare per respingere un’ipotesi.

Rappresenta la probabilità di respingere l’ipotesi nulla quando questa è in realtà vera, che è un tipo di errore noto come errore di tipo I o falso positivo.

Ad esempio, se un test è impostato con un livello di significatività del 5% (α = 0,05), significa che c’è un rischio del 5% di respingere l’ipotesi nulla quando questa è vera. Questo livello, 0,05, è una scelta comune per α, anche se possono essere utilizzati altri livelli, come 0,01 o 0,10, a seconda del contesto e del campo di studio.

Più piccola è la dimensione del test, più forte è la prova richiesta per respingere l’ipotesi nulla, riducendo la probabilità di un errore di tipo I ma potenzialmente aumentando la possibilità di un errore di tipo II (non riuscire a respingere l’ipotesi nulla quando questa è falsa). Il bilanciamento tra gli errori di tipo I e di tipo II è una considerazione importante nella progettazione di qualsiasi test statistico.

Dimensione empirica

La dimensione empirica nel contesto del test delle ipotesi tramite simulazioni Monte Carlo si riferisce alla proporzione di volte in cui l’ipotesi nulla viene erroneamente respinta nelle simulazioni quando l’ipotesi nulla è vera. Questa è essenzialmente una versione simulata del tasso di errore di tipo I.

Ecco un processo generale su come si farebbe questo:

1. Imposta la tua ipotesi nulla e scegli un livello di significatività per il tuo test (ad esempio, α = 0,05).

2. Genera un gran numero di campioni assumendo che l’ipotesi nulla sia vera. Il numero di campioni è di solito molto grande, come 10.000 o 100.000, per garantire la stabilità dei risultati.

3. Per ogni campione, effettua il test delle ipotesi e registra se l’ipotesi nulla è stata respinta (puoi registrarlo come 1 per la respinta e 0 per il mancato rifiuto).

4. Calcola la dimensione empirica come la proporzione di simulazioni in cui l’ipotesi nulla è stata respinta. Questo stima la probabilità di respingere l’ipotesi nulla quando è vera secondo la procedura di test data.

Il codice seguente mostra come implementare questo.

import numpy as np
from scipy.stats import ttest_1samp
import random
random.seed(10)

def calculate_empirical_size(num_simulations: int, sample_size: int, true_mean: float, significance_level: float) -> float:
    """
    Simula un insieme di campioni e conduce un test di ipotesi su ognuno, quindi calcola la dimensione empirica.
    Parametri:
    num_simulations (int): Il numero di simulazioni da eseguire.
    sample_size (int): La dimensione di ogni campione simulato.
    true_mean (float): La vera media nell'ipotesi nulla.
    significance_level (float): Il livello di significatività per i test di ipotesi.
    Restituisce:
    float: La dimensione empirica, ovvero la proporzione di test in cui l'ipotesi nulla è stata rifiutata.
    """
    import numpy as np
    from scipy.stats import ttest_1samp
    
    # Inizializza il contatore per i rifiuti dell'ipotesi nulla
    rejections = 0
    
    # Esegue le simulazioni
    np.random.seed(0)  # per riproducibilità
    for _ in range(num_simulations):
        sample = np.random.normal(loc=true_mean, scale=1, size=sample_size)
        t_stat, p_value = ttest_1samp(sample, popmean=true_mean)
        if p_value < significance_level:
            rejections += 1

    # Calcola la dimensione empirica
    empirical_size = rejections / num_simulations
    return empirical_size

calculate_empirical_size(1000, 1000, 0, 0.05)

Per ciascuna delle 1000 simulazioni, viene estratto un campione casuale di dimensione 1000 da una distribuzione normale con media 0 e deviazione standard 1. Viene quindi condotto un test t per campioni singoli per verificare se la media del campione differisce significativamente dalla vera media (0 in questo caso). Se il valore p del test è inferiore al livello di significatività (0,05), l’ipotesi nulla viene rifiutata.

La dimensione empirica viene calcolata come il numero di volte in cui l’ipotesi nulla viene rifiutata (il numero di falsi positivi) diviso per il numero totale di simulazioni. Questo valore dovrebbe essere vicino al livello di significatività nominale in un test ben calibrato. In questo caso, la funzione restituisce la dimensione empirica, che dà un’idea di quante volte è possibile rifiutare erroneamente l’ipotesi nulla quando è effettivamente vera nelle applicazioni reali, assumendo le stesse condizioni della simulazione.

A causa delle variazioni casuali, la dimensione empirica potrebbe non coincidere esattamente con il livello di significatività nominale, ma dovrebbero essere vicine se la dimensione del campione è sufficientemente grande e le ipotesi del test sono soddisfatte. Questa differenza tra la dimensione empirica e quella nominale è il motivo per cui vengono condotti studi di simulazione come questo, per vedere quanto bene la dimensione nominale corrisponde alla realtà.

<h2 id="

Esperimenti senza covariate nel DGP

Di seguito simuliamo dati che seguono un DGP in cui l’outcome è influenzato solo dal trattamento e da un errore casuale.

y_i = tau*T_i+e_i

Se l’outcome è influenzato solo dal trattamento, le stime del parametro dell’effetto del trattamento sono precise anche per dimensioni campionarie relativamente piccole e convergono rapidamente al vero valore del parametro all’aumentare della dimensione campionaria. Nel codice sottostante, il valore del parametro tau è impostato a 2.

tau = 2corr = .5p = 10p0 = 0 # numero di covariate utilizzate nel DGPNrange = range(10,1000,2) # ciclo sui valori di N(nvalues,tauhats,sehats,lb,ub) = fn_run_experiments(tau,Nrange,p,p0,corr)caption = """Stime del parametro dell'effetto del trattamento     per un esperimento randomizzato senza covariate"""fn_plot_with_ci(nvalues,tauhats,tau,lb,ub,caption)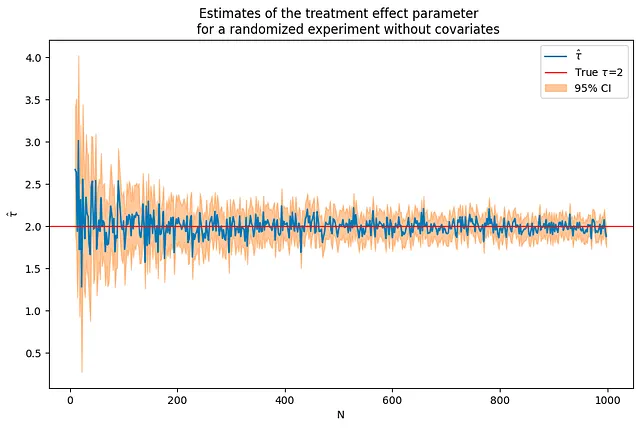

Per una determinata dimensione campionaria, verifica che questo sia lo stesso di eseguire una regressione con un’intercetta.

Puoi verificare che ottieni gli stessi risultati eseguendo una regressione OLS dell’outcome su un’intercetta e il trattamento.

N = 100Yexp,T = fn_generate_data(tau,N,10,0,corr)Yt = Yexp[np.where(T==1)[0],:]Yc = Yexp[np.where(T==0)[0],:]tauhat,se_tauhat = fn_tauhat_means(Yt,Yc)# n_values = n_values + [N]# tauhats = tauhats + [tauhat]lb = lb + [tauhat-1.96*se_tauhat]ub = ub + [tauhat+1.96*se_tauhat]print(f"Stima del parametro e errore standard ottenuti calcolando la differenza tra le medie:{tauhat:.5f},{se_tauhat:.5f}")const = np.ones([N,1])model = sm.OLS(Yexp,np.concatenate([T,const],axis = 1))res = model.fit()print(f"Stima del parametro e errore standard ottenuti eseguendo una regressione OLS con un'intercetta:{res.params[0]:.5f},{ res.HC1_se[0]:.5f}")

Stima del parametro e errore standard ottenuti calcolando la differenza tra le medie:1.91756,0.21187Stima del parametro e errore standard ottenuti eseguendo una regressione OLS con un'intercetta:1.91756,0.21187

Esegui iterazioni di Monte Carlo in R e calcola il bias, l’RMSE e la dimensione

Adesso eseguirai simulazioni di Monte Carlo in cui aumenti la dimensione campionaria ciclando su una lista di valori per il parametro N. Calcolerai l’RMSE, il bias e la dimensione empirica del test per ogni iterazione.

Questo script Python conduce una simulazione sperimentale per studiare come la dimensione campionaria (N) influisce sul bias, sull’RMSE e sulla dimensione delle performance del test A/B quando non vengono considerate covariate. Vediamo passo dopo passo:

1. estDict = {} inizializza un dizionario vuoto per memorizzare i risultati sperimentali.

2. R=2000 imposta il numero di ripetizioni per l’esperimento a 2000.

3. for N in [10,50,100,500,1000] cicla su diverse dimensioni campionarie.

4. All’interno di questo ciclo, tauhats=[], sehats=[] vengono inizializzate come liste vuote per memorizzare gli effetti del trattamento stimati tauhat e i loro errori standard corrispondenti se_tauhat per ogni esperimento.

5. for r in tqdm(range(R)): cicla su R esperimenti, con una barra di avanzamento fornita da tqdm.

6. Yexp,T = fn_generate_data(tau,N,10,0,corr) genera dati sintetici per ogni esperimento con un effetto del trattamento predefinito tau, un numero di osservazioni N, 10 covariate, nessuna covariata con coefficienti non nulli e una correlazione predefinita.

7. Yt=Yexp[np.where(T==1)[0],:]e Yc=Yexp[np.where(T==0)[0],;] separano i dati sintetici in gruppi trattati e di controllo.

8. tauhat,se_tauhat=fn_tauhat_means(Yt,Yc) calcola la stima dell’effetto del trattamento e il suo errore standard.

9. tauhats=tauhats+[tauhat]e sehats=sehats+[se_tauhat] aggiungono la stima dell’effetto del trattamento e il suo errore standard alle liste corrispondenti.

10. estDict[N]={‘tauhat':np.array(tauhats).reshape([len(tauahts),1]),’sehat':np.array(sehats).reshape([len(sehats),1])} memorizza le stime nel dizionario con la dimensione del campione come chiave.

11. tau0 = tau*np.ones([R,1]) crea un array di dimensione R con tutti gli elementi uguali al vero effetto del trattamento.

12. Per ogni dimensione del campione in estDict, lo script calcola e stampa il bias, il RMSE e la dimensione della stima dell’effetto del trattamento utilizzando la funzione fn_bias_rmse_size().

Come previsto, il bias e il RMSE diminuiscono all’aumentare della dimensione del campione, e la dimensione si avvicina alla dimensione reale, 0.05.

estDict = {}R = 2000for N in [10,50,100,500,1000]:    tauhats = []    sehats = []    for r in tqdm(range(R)):        Yexp,T = fn_generate_data(tau,N,10,0,corr)        Yt = Yexp[np.where(T==1)[0],:]        Yc = Yexp[np.where(T==0)[0],:]        tauhat,se_tauhat = fn_tauhat_means(Yt,Yc)        tauhats = tauhats + [tauhat]        sehats = sehats + [se_tauhat]    estDict[N] = {        'tauhat':np.array(tauhats).reshape([len(tauhats),1]),        'sehat':np.array(sehats).reshape([len(sehats),1])    }    tau0 = tau*np.ones([R,1])for N, results in estDict.items():    (bias,rmse,size) = fn_bias_rmse_size(tau0,results['tauhat'],                                         results['sehat'])    print(f'N={N}: bias={bias}, RMSE={rmse}, size={size}')

100%|██████████| 2000/2000 [00:00<00:00, 3182.81it/s]100%|██████████| 2000/2000 [00:00<00:00, 2729.99it/s]100%|██████████| 2000/2000 [00:00<00:00, 2238.62it/s]100%|██████████| 2000/2000 [00:04<00:00, 479.67it/s]100%|██████████| 2000/2000 [02:16<00:00, 14.67it/s]N=10: bias=0.038139125088721144, RMSE=0.6593256331782233, size=0.084N=50: bias=0.002694446014687934, RMSE=0.29664599979723183, size=0.0635N=100: bias=-0.0006785229668018156, RMSE=0.20246779253127453, size=0.0615N=500: bias=-0.0009696751953095926, RMSE=0.08985542730497854, size=0.062N=1000: bias=-0.0011137216061364087, RMSE=0.06156258265280801, size=0.047

Esperimenti con le variabili covariate nel DGP

Successivamente, aggiungerai le variabili covariate al DGP. Ora l’outcome di interesse dipende non solo dal trattamento ma anche da altre variabili X. Il codice sottostante simula dati con 50 covariate incluse nel DGP. Utilizzando le stesse dimensioni del campione e il parametro dell’effetto del trattamento della simulazione precedente senza covariate, è possibile vedere che questa volta le stime sono molto più rumorose, ma convergono comunque alla soluzione corretta.

y_i = tau*T_i + beta*x_i + e_i

Il grafico sottostante confronta le stime dei due DGP – puoi vedere quanto più rumorose siano le stime quando vengono introdotti i covariati nel DGP.

tau = 2corr = .5p = 100p0 = 50 # numero di covarianti utilizzate nel DGP Nrange = range(10,1000,2) # iterazione sui valori di N (nvalues_x,tauhats_x,sehats_x,lb_x,ub_x) = fn_run_experiments(tau,Nrange,p,p0,corr)caption = """Stime del parametro dell'effetto del trattamento per un esperimento randomizzato con X nel DGP ma nessun X incluso nell'estimatore"""fn_plot_with_ci(nvalues_x,tauhats_x,tau,lb_x,ub_x,caption)# esegui nuovamente l'esperimento senza covariantip0 = 0 # numero di covarianti utilizzate nel DGP Nrange = range(10,1000,2) # iterazione sui valori di N (nvalues_x0,tauhats_x0,sehats_x0,lb_x0,ub_x0) = fn_run_experiments(tau,Nrange,p,p0,corr)fig = plt.figure(figsize = (10,6))plt.title("""Stime del parametro dell'effetto del trattamento per un esperimento randomizzato con X nel DGP ma nessun X incluso nell'estimatore, zoom per N grandi""")plt.plot(nvalues_x[400:],tauhats_x[400:],label = '$\hat{\\tau}^{(x)}$')plt.plot(nvalues_x[400:],tauhats_x0[400:],label = '$\hat{\\tau}$',color = 'green')plt.legend()fig = plt.figure(figsize = (10,6))plt.title("""Stime dell'effetto del trattamento dal DGP con e senza covarianti, zoom per N grandi""")plt.plot(nvalues_x[400:],tauhats_x[400:],label = '$\hat{\\tau}^{(x)}$')plt.plot(nvalues_x[400:],tauhats_x0[400:],label = '$\hat{\\tau}$',color = 'green')plt.legend()

100%|██████████| 495/495 [00:41<00:00, 12.06it/s]100%|██████████| 495/495 [00:42<00:00, 11.70it/s]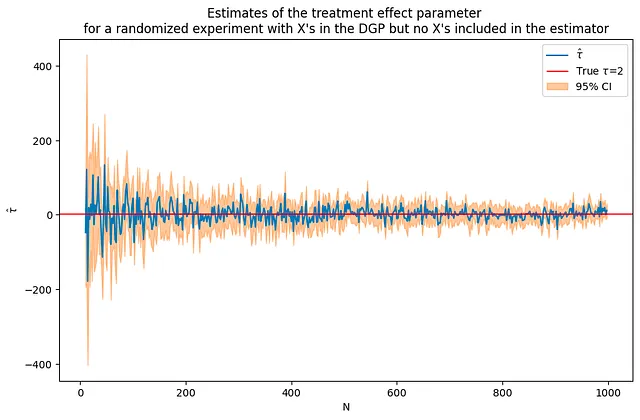

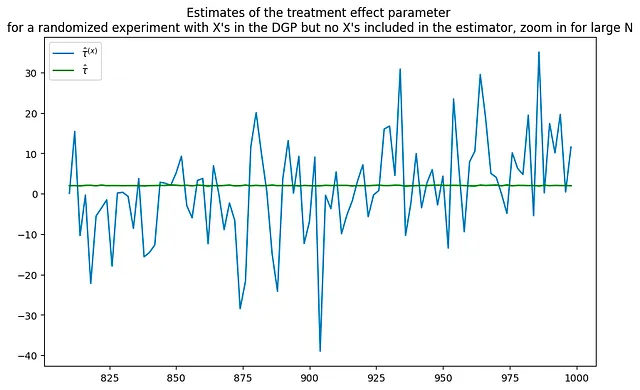
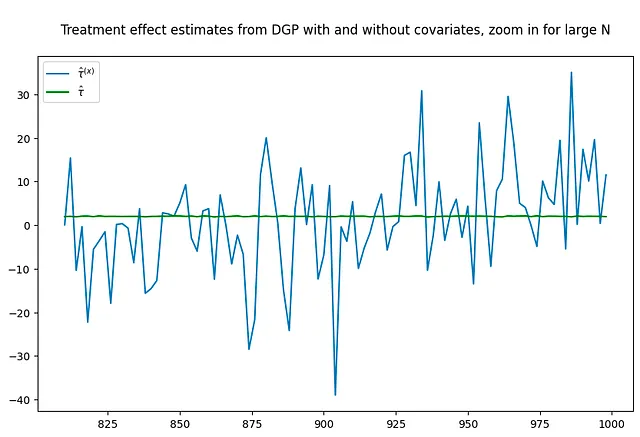
Ripetere l’esperimento con una dimensione del campione molto più grande allevia il problema? Non necessariamente. Nonostante l’aumento della dimensione del campione, le stime appaiono ancora abbastanza rumorose.

tau = 2corr = .5p = 100p0 = 50 # numero di covarianti utilizzate nel DGP Nrange = range(1000,50000,10000) # iterazione sui valori di N (nvalues_x2,tauhats_x2,sehats_x2,lb_x2,ub_x2) = fn_run_experiments(tau,Nrange,p,p0,corr)fn_plot_with_ci(nvalues_x2,tauhats_x2,tau,lb_x2,ub_x2,caption)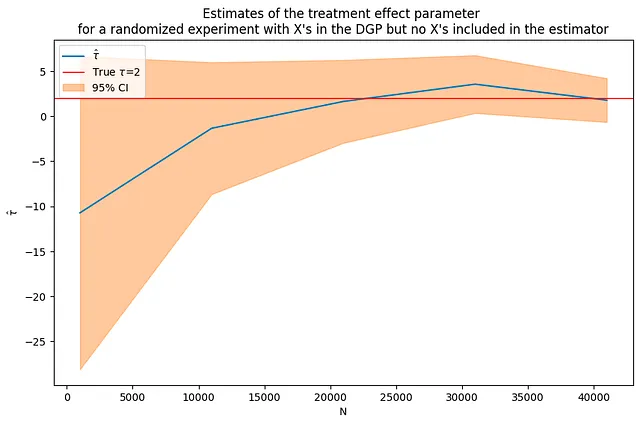

DGP con X – aggiunta di covarianti alla regressione

In questa parte, userai lo stesso DGP di prima:

y_i = tau*T_i + beta*x_i + e_i

Ora includerai queste covarianti X nel modello di regressione. Troverai che questo migliora significativamente la precisione delle stime. Tuttavia, tieni presente che questo è un po’ una “frode” – in questo caso, hai incluso le covarianti corrette fin dall’inizio.

In uno scenario reale, potrebbe non essere noto quali covariate siano quelle “giuste” da includere, e potrebbe essere necessario sperimentare con diversi modelli e covariate.

tau = 2corr = .5p = 100p0 = 50 # numero di covariate utilizzate nel DGPNrange = range(100,1000,2) # ciclo sui valori di N# abbiamo bisogno di iniziare con più osservazioni rispetto a pflagX = 1(nvalues2,tauhats2,sehats2,lb2,ub2) = fn_run_experiments(tau,Nrange,p,p0,corr,flagX)caption = """Stime del parametro dell'effetto del trattamento per un esperimento randomizzato con X nel DGP, stime ottenute utilizzando la regressione con le giuste X"""fn_plot_with_ci(nvalues2,tauhats2,tau,lb2,ub2,caption)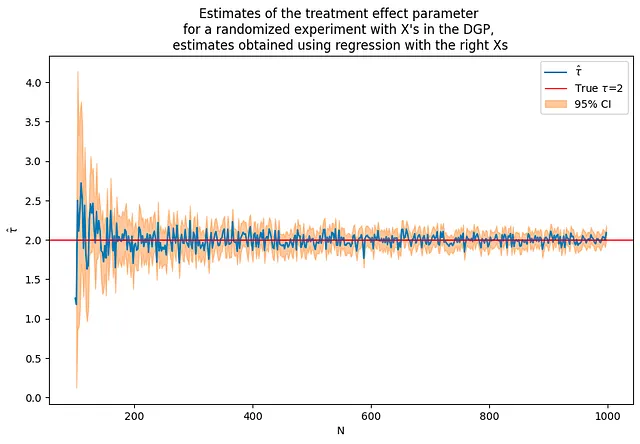

Cosa succede se si utilizzano alcune X che influenzano l’outcome e alcune che non lo fanno?

Questa sezione esamina l’inclusione di alcune covariate rilevanti e alcune non rilevanti in un modello di regressione. Ciò simula uno scenario reale in cui potrebbe non essere chiaro quali covariate influenzino l’outcome.

Anche se vengono incluse alcune variabili non influenti, si può osservare che la stima complessiva tende a migliorare rispetto al caso in cui non venivano incluse covariate. Tuttavia, l’inclusione di variabili non rilevanti può introdurre del rumore e dell’incertezza nelle stime, e potrebbero non essere così precise come quando venivano incluse solo le covariate rilevanti.

In conclusione, comprendere l’influenza delle covariate nei dati è essenziale per migliorare la precisione e l’affidabilità dei risultati dei test A/B. Questo tutorial esplora le proprietà statistiche degli stimatori come RMSE, bias e size e dimostra come possono essere stimati e compresi attraverso simulazioni Monte Carlo. Mette anche in evidenza l’impatto dell’inclusione delle covariate nel DGP e nei modelli di regressione, sottolineando l’importanza di una selezione attenta del modello e di test di ipotesi nella pratica.

# Usa lo stesso DGP come precedentetau = 2corr = .5p = 100p0 = 50 # numero di covariate utilizzate nel DGPa = 0.9b = 0.1Nrange = range(100,1000,2) # ciclo sui valori di N# abbiamo bisogno di iniziare con più osservazioni rispetto a pflagX = 2(nvalues3,tauhats3,sehats3,lb3,ub3) = fn_run_experiments(tau,Nrange,p,p0,corr,flagX,a,b)caption = f"""Stime del parametro dell'effetto del trattamento per un esperimento randomizzato con X nel DGP, stime ottenute utilizzando la regressione con il {100*a:.1f}% delle X corrette e il {100*b:.1f}% delle X non rilevanti"""fn_plot_with_ci(nvalues3,tauhats3,tau,lb3,ub3,caption)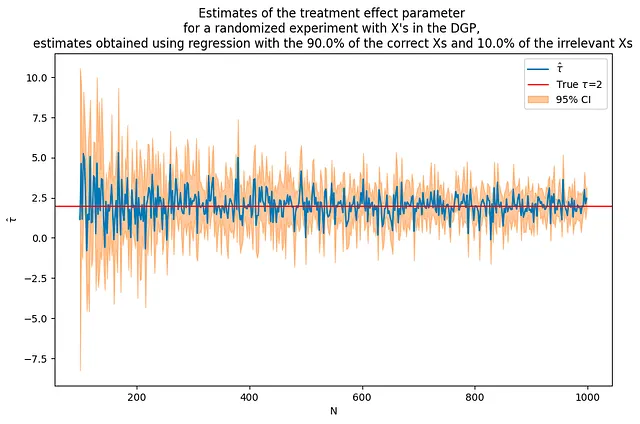

Se non diversamente indicato, tutte le immagini sono dell’autore.