Una Derivazione Accessibile della Regressione Lineare

Una Derivazione Accessibile della Regressione Lineare' can be condensed to 'Derivazione Regressione Lineare Accessibile'.

La matematica dietro il modello, dalle assunzioni additive alle matrici pseudoinverse

Avvertenza tecnica: È possibile derivare un modello senza assumere la normalità. Seguiremo questa strada perché è abbastanza semplice da comprendere e assumendo la normalità dell’output del modello, possiamo ragionare sull’incertezza delle nostre previsioni.

Questo post è rivolto a persone che sono già a conoscenza di cosa sia la regressione lineare (e forse l’hanno utilizzata una o due volte) e desiderano una comprensione più basata sui principi della matematica che sta dietro ad essa.

Un po’ di background sulla probabilità di base (distribuzioni di probabilità, probabilità congiunte, eventi mutualmente esclusivi), algebra lineare e statistica probabilmente sono necessari per cogliere al meglio ciò che segue. Senza ulteriori indugi, eccoci qui:

Il mondo dell’apprendimento automatico è pieno di connessioni sorprendenti: la famiglia esponenziale, la regolarizzazione e le credenze precedenti, KNN e SVM, Maximum Likelihood e Information Theory – è tutto collegato! (Amo Dark). Questa volta discuteremo come derivare un altro membro della famiglia esponenziale: il modello di regressione lineare, e nel processo vedremo che la funzione di perdita Mean Squared Error è teoricamente ben motivata. Come per qualsiasi modello di regressione, saremo in grado di utilizzarlo per prevedere obiettivi numerici e continui. È un modello semplice ma potente che si rivela uno dei cavalli di battaglia dell’inferenza statistica e del design sperimentale. Tuttavia, ci preoccuperemo solo del suo utilizzo come strumento predittivo. Nessun fastidioso inferenza (e Dio non voglia, causale) qui.

• Incontra CoDeF un modello di Intelligenza Artificiale (AI) che ti consente di fare editing di stile video realistico, tracciamento basato sulla segmentazione e super risoluzione video.
• Arte e Identità Il Profondo Legame tra Rilevanza Personale e Attrattiva Estetica Svelato dall’IA
• Come i fornitori di servizi gestiti possono rimanere rilevanti nell’era dell’AI

Ok, cominciamo. Vogliamo prevedere qualcosa basandoci su qualcos’altro. Chiameremo la cosa prevista y e il qualcos’altro x. Come esempio concreto, vi offro la seguente situazione fittizia: siete analisti di credito che lavorano in una banca e siete interessati a trovare automaticamente il limite di credito corretto per un cliente bancario. Avete anche a disposizione un dataset relativo a clienti passati e quale limite di credito (la cosa prevista) è stato approvato per loro, insieme ad alcune loro caratteristiche come informazioni demografiche, passato rendimento del credito, reddito, ecc. (il qualcos’altro).

Quindi abbiamo una grande idea e scriviamo un modello che spiega il limite di credito in termini di tali caratteristiche disponibili, con l’assunzione principale del modello che ciascuna caratteristica contribuisce qualcosa all’output osservato in modo additivo. Poiché il discorso sul credito era solo un esempio motivante (e artificioso), torniamo al nostro mondo di vacche sferiche della matematica pura, con il nostro modello che diventa qualcosa di simile a questo:

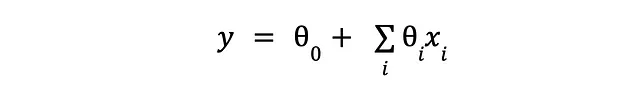
Abbiamo ancora la cosa prevista (y) e il qualcos’altro che usiamo per prevederlo (x). Ammettiamo che qualche tipo di rumore sia inevitabile (sia per virtù di una misurazione imperfetta o della nostra stessa cecità) e il meglio che possiamo fare è assumere che il modello dietro ai dati che osserviamo sia stocastico. La conseguenza di ciò è che potremmo vedere output leggermente diversi per lo stesso input, quindi invece di stime puntuali ordinate siamo “bloccati” con una distribuzione di probabilità sugli output (y) condizionata agli input (x):

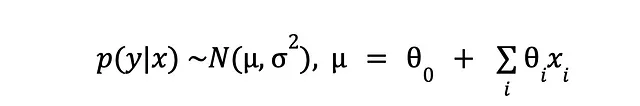
Ogni punto dati in y viene sostituito da una piccola curva a campana, la cui media si trova nei valori osservati di y, e ha una varianza di cui al momento non ci importa. Quindi il nostro piccolo modello prenderà il posto della media della distribuzione.

Assumendo che tutte quelle curve a campana siano effettivamente distribuzioni normali e che le loro medie (punti dati in y) siano indipendenti l’una dall’altra, la probabilità (congiunta) di osservare il dataset è

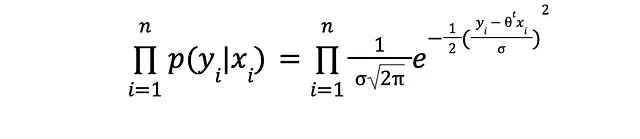
I logaritmi e un po’ di algebra ci salvano:

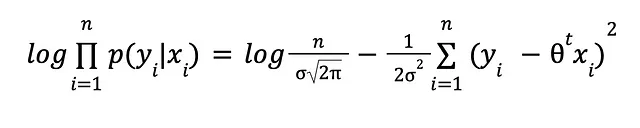
I logaritmi sono fantastici, vero? I logaritmi trasformano la moltiplicazione in somma, la divisione in sottrazione e le potenze in moltiplicazione. Piuttosto utili sia dal punto di vista algebrico che numerico. Eliminando le costanti, che in questo caso sono irrilevanti, arriviamo al seguente problema di massima verosimiglianza:

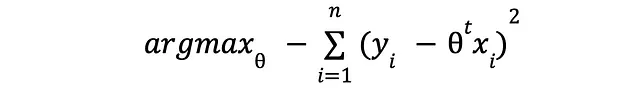
Bene, è la stessa cosa di

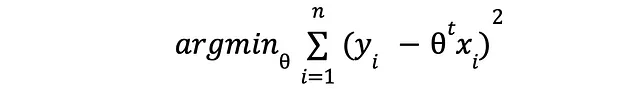
L’espressione che stiamo per minimizzare è molto simile alla famosa perdita del Mean Square Error. Infatti, ai fini dell’ottimizzazione, sono equivalenti.

Quindi, adesso che facciamo? Questo problema di minimizzazione può essere risolto esattamente usando le derivate. Approfitteremo del fatto che la perdita è quadratica, il che significa convessa, il che significa un solo minimo globale; ci permette di prendere la sua derivata, impostarla a zero e risolvere per theta. Facendo questo troveremo il valore dei parametri theta che rende la derivata della perdita zero. E perché? perché è precisamente nel punto in cui la derivata è zero che la perdita è al minimo.

Per semplificare il tutto, esprimiamo la perdita in notazione vettoriale:

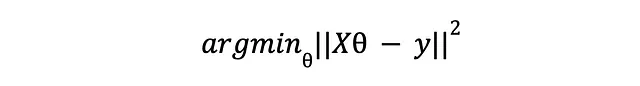
Qui, X è una matrice NxM che rappresenta l’intero set di dati di N esempi e M caratteristiche e y è un vettore che contiene le risposte attese per ogni esempio di allenamento. Prendendo la derivata e impostandola a zero otteniamo

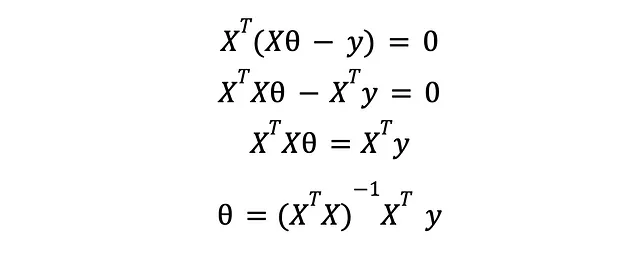
Ecco, abbiamo la soluzione al problema di ottimizzazione in cui abbiamo trasformato il nostro problema di apprendimento automatico originale. Se vai avanti e inserisci quei valori dei parametri nel tuo modello, avrai un modello di apprendimento automatico addestrato pronto per essere valutato utilizzando un set di dati di controllo (o forse attraverso la convalida incrociata).

Se pensi che l’espressione finale assomigli terribilmente alla soluzione di un sistema lineare,

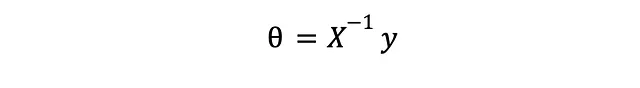
è perché lo è. Le cose extra derivano dal fatto che per il nostro problema sia equivalente a un sistema lineare normale, avremmo bisogno di un numero uguale di caratteristiche ed esempi di allenamento in modo da poter invertire X. Poiché questo è raramente il caso, possiamo solo sperare in una soluzione “migliore” – in un certo senso – ricorrendo alla pseudoinversa di Moore-Penrose di X, che è una generalizzazione della vecchia matrice inversa. L’articolo associato su Wikipedia è interessante da leggere.

Una piccola incursione nella regolarizzazione

D’ora in poi, assumerò che tu abbia sentito il termine “regolarizzazione” da qualche parte e forse sai cosa significa. In ogni caso, ti dirò come lo interpreto io: la regolarizzazione è qualsiasi cosa tu faccia a un modello che migliora le sue prestazioni al di fuori del campione a scapito di prestazioni peggiori all’interno del campione. Perché tutto ciò è importante? perché alla fine, le prestazioni fuori campione (cioè nella vita reale) sono ciò che conta – a nessuno interesserà quanto sia basso l’errore di allenamento o quanto sia incredibile l’AUC sul set di allenamento a meno che il tuo modello non si comporti in modo comparativamente buono in produzione. E abbiamo scoperto che se non siamo attenti, ci imbatteremo in qualcosa chiamato sovradattamento, dove il tuo modello memorizza l’intero set di allenamento fino al rumore, diventando potenzialmente inutile per le previsioni fuori campione. Sappiamo anche che c’è un compromesso tra la complessità del modello e le prestazioni fuori campione (teoria dell’apprendimento statistico di Vapnik) e la regolarizzazione può essere vista come un tentativo di mantenere sotto controllo la complessità del modello nella speranza di ottenere migliori capacità di generalizzazione (qui la generalizzazione è un altro nome per le prestazioni fuori campione).

La regolarizzazione può assumere molte forme, ma per gli scopi di questo articolo discuteremo solo un approccio che viene spesso utilizzato per i modelli di regressione lineare. Ricorda che ho detto che con la regolarizzazione stiamo cercando di mantenere sotto controllo la complessità, giusto? Beh, la complessità indesiderata può insinuarsi principalmente in due modi: 1. troppi attributi di input e 2. valori elevati per i loro corrispondenti valori di theta. Risulta che qualcosa chiamato regolarizzazione L2 può aiutare in entrambi i casi. Ricordi la nostra perdita?

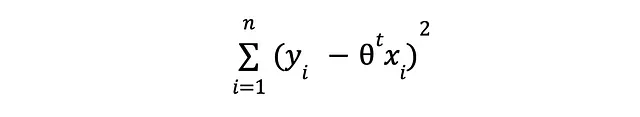
eravamo preoccupati solo di minimizzare le differenze quadrate tra i valori predetti e osservati di y, senza considerare altro. Questo focus miope potrebbe essere un problema perché potresti in teoria manipolare il sistema e continuare ad aggiungere attributi fino a quando l’errore diventa minimo, anche se quegli attributi extra non hanno nulla a che fare con il segnale che stiamo cercando di apprendere. Se avessimo una conoscenza perfetta delle cose rilevanti per il nostro problema, non includeremmo attributi inutili! (a dire il vero, non useremmo l’apprendimento automatico in primo luogo, ma mi dilungo). Per compensare la nostra ignoranza e mitigare il rischio di introdurre tale complessità indesiderata, aggiungeremo un termine extra alla perdita:

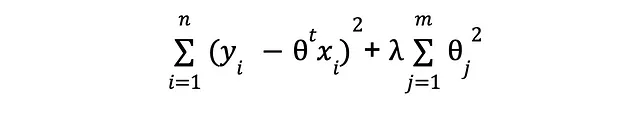
Cosa fa, potresti chiedere. Te lo dirò – abbiamo appena introdotto un incentivo per mantenere la magnitudine dei parametri il più vicino possibile allo zero. In altre parole, vogliamo mantenere la complessità al minimo. Ora, invece di avere un solo obiettivo (la minimizzazione degli errori di previsione), ne abbiamo uno in più (la minimizzazione della complessità), e la soluzione per il problema complessivo dovrà bilanciare entrambi. Abbiamo un ruolo nel determinare come appare quel bilanciamento, attraverso quel nuovo e brillante coefficiente lambda: più grande è, più importanza diamo all’obiettivo di bassa complessità.

Quello è molto discorso. Vediamo cosa fa il termine extra al theta ottimale. La nuova perdita in forma vettorializzata è

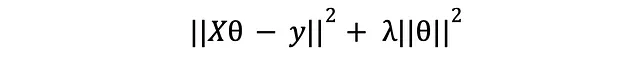
prendendo la sua derivata, impostandola a zero e risolvendo per theta:

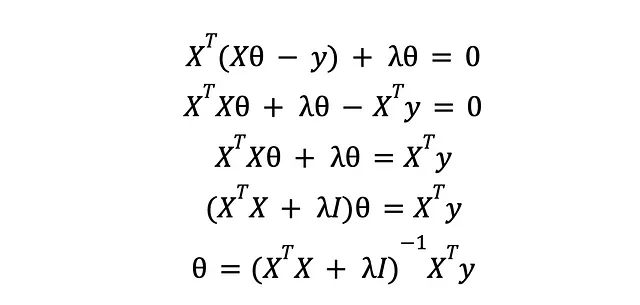
Risulta che la nuova soluzione non è troppo diversa dalla precedente. Abbiamo una matrice diagonale extra che si occuperà di eventuali problemi di rango che ci impedirebbero di invertire la matrice XTX, aggiungendo un po’ di “rumore” al mix. Ciò illumina un altro modo in cui potrebbe essere introdotta una complessità non necessaria: attributi col lineari, cioè attributi che sono trasformazioni lineari (versioni scalate e spostate) di altri attributi. Per quanto riguarda la regressione lineare, due attributi col lineari sono lo stesso attributo, contano come una sola colonna, e l’attributo extra non aggiunge nuove informazioni utili per addestrare il nostro modello; rendendo la matrice XTX di rango ridotto, cioè impossibile da invertire. Con la regolarizzazione, in ogni riga di XTX, una colonna diversa è influenzata da lambda, il rumore – impedendo qualsiasi possibile collinearità e rendendola a rango completo. Vediamo che aggiungere cose casuali come predittori potrebbe effettivamente rovinare l’intero processo di apprendimento. Fortunatamente, la regolarizzazione è qui per salvare la giornata (per favore, non fraintendete il mio elogio della regolarizzazione come un invito a essere negligenti nella selezione dei predittori – non lo è).

Ecco quindi un modello di regressione lineare regolarizzato pronto all’uso. Da qui, dove andiamo? beh, potresti approfondire l’idea che la regolarizzazione codifica una convinzione precedente sullo spazio dei parametri, rivelando la sua connessione con l’inferenza bayesiana. Oppure potresti approfondire la sua connessione con le macchine a vettori di supporto e alla fine con modelli non parametrici come KNN. Inoltre, potresti riflettere sul fatto che tutti quei gradienti eleganti dalla regressione lineare e logistica sembrano sospettosamente simili. Puoi stare tranquillo, affronterò questi argomenti in un futuro post!