Comprendere meglio i test A/B capire meglio con domande difficili

'Migliorare la comprensione dei test A/B attraverso domande difficili'

Svelare gli aspetti controintuitivi del testing A/B tramite domande sfide, migliorare la tua comprensione ed evitare errori

Questo articolo evidenzia gli errori statistici comuni nel contesto degli esperimenti. È strutturato come cinque domande con risposte che molti trovano controintuitive. È pensato per coloro che sono già familiari con i test A/B ma che vogliono ampliare la propria comprensione. Questo può aiutarti a evitare errori comuni nel tuo lavoro quotidiano o a superare un colloquio di lavoro.

Domanda 1: Hai condotto un test A/B (α = 0.05, β = 0.2), che produce un risultato statisticamente significativo. In questo scenario, qual è la probabilità che sia un vero positivo?

Immagina se dovessi misurare solo le ipotesi di lavoro. Allora, il 100% dei test A/B di successo sarebbe vero positivo. Quando nessuna delle tue ipotesi funziona, il 100% dei test A/B di successo sarebbe falso positivo.

Questi due estremi sono destinati a dimostrare che è impossibile rispondere a questa domanda senza un passaggio aggiuntivo, ovvero un’ipotesi sulla distribuzione delle ipotesi.

• Come chiamare Hugging Face AI da un database Oracle utilizzando JavaScript
• Progetto di Data Science per la predizione delle valutazioni dei film di Rotten Tomatoes Secondo Approccio
• LangChain Consenti a LLM di interagire con il tuo codice

Proviamo ancora una volta e supponiamo che il 10% delle ipotesi che testiamo sia efficace. Allora, osservare un risultato statisticamente significativo da un test A/B implica che ci sia una probabilità del 64% (secondo il teorema di Bayes, (1–0.2)*0.1 / ((1–0.2)*0.1 + 0.05*(1–0.1))) che sia un vero positivo.

Domanda 2: Supponi che l’ipotesi nulla sia vera. In questa circostanza, una p-value più alta o più bassa sarebbe più probabile?

Molti pensano che sia la prima opzione. Questo sembra intuitivo: quando non c’è effetto, il risultato è più probabile che sia lontano dalla significatività statistica, quindi una p-value più alta.

Tuttavia, la risposta è nessuna delle due. Quando l’ipotesi nulla è vera, le p-value sono distribuite uniformemente.

La confusione sorge perché le persone spesso visualizzano questi concetti in termini di z-score, o medie campionarie, o differenze tra medie campionarie. Tutti questi sono distribuiti normalmente. Potrebbe essere difficile comprendere, quindi, l’uniformità delle p-value.

Illustreremo questo con una simulazione. Supponiamo che sia il gruppo di trattamento che il gruppo di controllo siano estratti dalla stessa distribuzione normale (μ = 0, σ = 1), il che significa che l’ipotesi nulla è vera. Confronteremo quindi le loro medie, calcoleremo le p-value e ripeteremo questo processo più volte. Per semplicità, concentriamoci solo su casi in cui la media del gruppo di trattamento era più grande. E poi, concentriamoci su casi con p-value da 0.9 a 0.8 e da 0.2 a 0.1.

Quando mappiamo questi intervalli di p-value sulla distribuzione che abbiamo simulato, l’immagine diventa più chiara. Anche se il picco della distribuzione vicino allo zero è più alto, la larghezza dell’intervallo qui è più stretta. Al contrario, man mano che ci allontaniamo da zero, il picco si riduce ma la larghezza degli intervalli aumenta. Questo perché le p-value vengono calcolate in modo che intervalli di lunghezza uguale includano la stessa area sotto la curva.

Domanda 3: A causa di alcuni vincoli tecnici o commerciali, hai eseguito un test A/B con una dimensione del campione inferiore alla norma. Il risultato è appena significativo. Tuttavia, la dimensione dell’effetto è grande, più grande di quanto di solito si veda in test A/B simili. La dimensione dell’effetto più grande dovrebbe rafforzare la tua fiducia nel risultato?

Non proprio. Affinché un effetto venga classificato come significativo, deve essere a più o meno 2 errori standard da zero (quando α = 0.05). Man mano che la dimensione del campione diminuisce, gli errori standard aumentano generalmente. Ciò implica che gli effetti statisticamente significativi osservati in campioni più piccoli tendono ad essere più grandi.

La simulazione di seguito dimostra che: queste sono dimensioni degli effetti assoluti dei test A/B significativi quando entrambi i gruppi (N=1000) sono campionati dalla stessa distribuzione normale (μ = 0, σ = 1).

Domanda 4: Approfondiamo la comprensione ottenuta dalla domanda precedente. È possibile rilevare un vero effetto inferiore a 2 errori standard?

Sì, anche se la semantica qui è confusa . La dimensione dell’effetto vero potrebbe essere significativamente inferiore a 2 errori standard. Anche in questo caso, ci si aspetterebbe che una certa frazione dei test A/B presenti significatività statistica.

Tuttavia, in queste condizioni, la dimensione dell’effetto rilevata è sempre esagerata. Immaginiamo che il vero effetto sia 0.4, ma tu hai rilevato un effetto di 0.5 con un valore di p pari a 0.05. Considereresti questo un vero positivo? E se la dimensione dell’effetto vero è solo 0.1, ma hai rilevato ancora un effetto di 0.5? È ancora un vero positivo se l’effetto vero è solo 0.01?

Visualizziamo questa situazione. I gruppi di controllo (N=100) sono campionati da una distribuzione normale (μ = 0, σ = 2), mentre i gruppi di trattamento (N=100) sono campionati dalla stessa distribuzione ma con μ che varia da 0.1 a 1. Indipendentemente dalla dimensione dell’effetto vero, un test A/B di successo genera una dimensione dell’effetto stimata di almeno 0.5. Quando gli effetti veri sono inferiori a questo valore, la stima risultante è chiaramente sovrastimata.

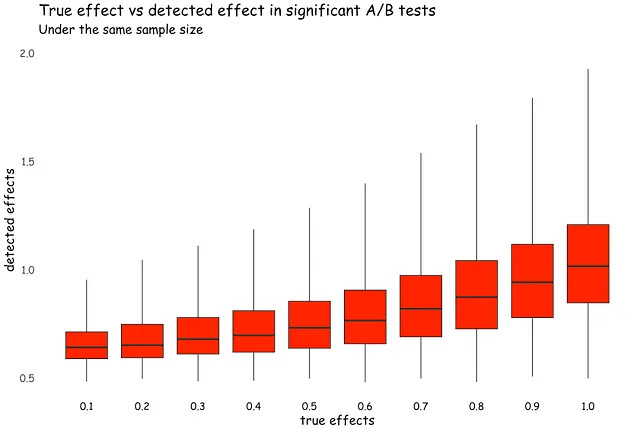
Ecco perché alcuni statistici evitano di dividere gli esiti in categorie binarie come “veri positivi” o “falsi positivi”. Invece, li trattano in modo più continuo [1].

Domanda 5: Hai condotto un test A/B che produce un risultato significativo, con un valore di p pari a 0.04. Tuttavia, il tuo capo rimane scettico e chiede un secondo test. Questo secondo test non restituisce un risultato significativo, presentando un valore di p pari a 0.25. Questo significa che l’effetto originale non era reale e il risultato iniziale era un falso positivo?

C’è sempre un rischio nell’interpretare i valori di p come una regola decisionale binaria e lexicografica. Ricordiamoci cosa è effettivamente un valore di p. È una misura di sorpresa. Ed è casuale e continuo. Ed è solo una parte delle evidenze.

Immagina che il primo esperimento (p=0.04) sia stato eseguito su 1.000 utenti. Il secondo (p=0.25) – su 10.000 utenti. Oltre alle evidenti differenze di qualità, il secondo test A/B, come abbiamo discusso nelle domande 3 e 4, probabilmente aveva una dimensione dell’effetto stimata molto più piccola che potrebbe non essere più praticamente significativa.

Invertiamo questa situazione: il primo (p=0.04) è stato eseguito su 10.000, e il secondo (p=0.25) – su 1.000 utenti. Qui siamo molto più sicuri che l’effetto “esista”.

Ora, immagina che entrambi i test A/B fossero identici. In questa situazione, hai osservato due risultati abbastanza simili, sorprendenti, nessuno dei quali è troppo coerente con l’ipotesi nulla. Il fatto che cadano da lati opposti di 0.05 non è molto importante. Quello che conta è che osservare due valori di p piccoli consecutivamente quando l’ipotesi nulla è vera è improbabile.

Una domanda che potremmo considerare è se questa differenza è statisticamente significativa di per sé. Categorizzare i valori di p in modo binario distorce la nostra intuizione, facendoci credere che ci sia una differenza vasta, persino ontologica, tra i valori di p su diversi lati del limite. Tuttavia, il valore di p è una funzione piuttosto continua e potrebbe essere possibile che due test A/B, nonostante diversi valori di p, presentino prove molto simili contro l’ipotesi nulla [2].

Un altro modo per guardare a ciò è combinare le evidenze. Supponendo che l’ipotesi nulla sia vera per entrambi i test, il valore di p combinato si attesta allo 0.05, secondo il metodo di Fisher. Ci sono altri metodi per combinare i valori di p, ma la logica generale rimane la stessa: un’ipotesi nulla rigida non è un’ipotesi realistica nella maggior parte delle situazioni. Pertanto, abbastanza esiti “sorprendenti”, anche se nessuno di essi è statisticamente significativo individualmente, potrebbero essere sufficienti per respingere l’ipotesi nulla.

Conclusioni

Il framework del Test di Ipotesi Nulla, che comunemente utilizziamo per analizzare i test A/B, non è particolarmente intuitivo. Senza una pratica mentale regolare, spesso ricorriamo a una comprensione “intuitiva” che può essere fuorviante. Possiamo anche sviluppare delle routine per facilitare questo onere cognitivo. Purtroppo, queste routine diventano spesso un po’ ritualistiche, con l’aderenza a procedure formali che oscurano l’obiettivo effettivo dell’inferenza.

Riferimenti

1. McShane, B. B., Gal, D., Gelman, A., Robert, C., & Tackett, J. L. (2019). Abbandonare la significatività statistica. The American Statistician , 73 (sup1), 235–245.
2. Gelman, A., & Stern, H. (2006). La differenza tra “significativo” e “non significativo” non è in sé statisticamente significativa. The American Statistician , 60 (4), 328–331.