Rubik e Markov

Rubik e Markov

Qui otteniamo la probabilità di risolvere ottimamente il Cubo di Rubik

Il Cubo di Rubik è un prototipo di problema di pianificazione con uno spazio di stato colossale e solo una soluzione. È la stessa definizione di cercare un ago in un pagliaio. Senza alcuna guida (anche se puoi girare le facce 100 volte al secondo) potresti passare l’intera età dell’universo senza successo. Tutto ciò che lo riguarda sembra coinvolgere numeri enormi.

La quantità che calcoleremo qui è un’eccezione a ciò. Con essa otterrai una prospettiva semplice su un problema difficile (e su qualsiasi problema di pianificazione simile). Abbiamo bisogno di due ingredienti, un processo casuale e un risolutore ottimale. Quest’ultimo è un dispositivo (reale o ideale) in grado di risolvere il cubo (o un problema simile) utilizzando un numero minimo di mosse, dato qualsiasi stato iniziale. Risponderemo completamente alla seguente domanda:

Se un cubo risolto subisce N mosse casuali, qual è la probabilità p(d|N) che un risolutore ottimale abbia bisogno esattamente di d mosse per risolverlo nuovamente?

In una situazione normale, se qualcuno ti chiede di risolvere il cubo, otterrai semplicemente quello, un cubo scombinato senza riferimenti o etichette. Qui abbiamo una informazione sullo stato scombinato: è stato ottenuto dopo N mosse casuali dallo stato risolto. Quell’informazione è utile!

• Dalla carta al pixel Valutazione delle migliori tecniche per la digitalizzazione di testi scritti a mano
• GraphReduce Utilizzando i grafi per astrazioni di ingegneria delle caratteristiche
• Robot Soft senza cervello naviga in ambienti complessi in una svolta nella robotica

Perché siamo interessati a p(d|N) ?

Computazionalmente puoi cercare di decifrare il cubo in modi diversi. L’ambizione di un progetto sul Cubo di Rubik potrebbe variare tra la risoluzione di uno o alcuni stati in modo subottimale e la risoluzione di ogni possibile stato in modo ottimale (questo richiederebbe, ad esempio, i famosi 35 anni-CPU). Un risolutore del cubo coinvolge generalmente due cose, un algoritmo di ricerca e una funzione euristica. Scegliendo queste due cose parametrizziamo quanto sia difficile, efficiente o computazionalmente impegnativo il nostro approccio.

Nel campo della funzione euristica, cioè la guida alla ricerca, c’è sempre spazio per nuove idee. Storicamente, l’euristica del cubo era una combinazione di stime di distanza simili a Manhattan per la posizione dei tasselli del cubo scombinato rispetto alle loro posizioni risolte. Solo di recente una rete neurale è stata utilizzata come euristica.

Rete neurale = nuova euristica del Cubo di Rubik

Il lavoro della rete neurale è semplice (un classificatore): le dai in input lo stato di un cubo x e viene prevista la profondità d di quello stato. La profondità d di uno stato è definita come il numero minimo di mosse necessarie per risolvere ottimamente il cubo da quell

training_data = (x , N).

Hanno preso d come N. Quella scelta è stata compensata migliorando dinamicamente l’accuratezza delle etichette utilizzando un loop simile a quello di Bellman durante l’allenamento. La probabilità p(d|N) calcolata qui offre un punto di partenza migliore per l’accuratezza di quei dati di addestramento (ottenuti abbondantemente semplicemente ruotando casualmente lo stato risolto N volte).

Una visione del Random Walk

Calcolare p(d|N) è equivalente a chiedersi quanto lontano sarebbe un camminatore casuale dopo N passi. Invece di camminare in una griglia quadrata, camminerebbe in un enorme grafo di Rubik con 10 alla potenza di 19 nodi (stati del cubo) e un numero simile di collegamenti (mosse legali). Se scegliamo una disposizione in cui i nodi sono organizzati in base alla loro profondità: con lo stato risolto al centro e gli stati di profondità d situati a una distanza d dal centro, il grafico apparirà molto simmetrico. La direzione radiale (profondità) offre una prospettiva molto semplice.

Convenzione

Qui adottiamo la cosiddetta metrica dei quarti di giro per il cubo 3x3x3, in cui una mossa coinvolge una rotazione di 90 gradi del lato, sia in senso orario che antiorario. In questa metrica ci sono dodici mosse possibili. Se avessimo scelto una metrica diversa, come la metrica dei mezzi giri (che include anche le rotazioni di 180 gradi come singola mossa), l’espressione per p(d|N) sarebbe diversa.

I dati

Per ottenere p(d|N) avremo bisogno di utilizzare una qualche forma di conoscenza di dominio, ma non vogliamo occuparci di grafi, database di pattern o teoria dei gruppi. Useremo qualcosa di più “primario”:

La lista che contiene la popolazione degli stati del cubo a una profondità d.

La lista (fornita dagli autori dell’articolo “Numero di Dio” del 2012) non specifica quali stati si trovano a una certa profondità, solo il numero totale di essi, e non c’è alcun riferimento a qualsiasi N.

# Lista di popolazione di profondità# numero di stati del cubo a una profondità d nella metrica dei quarti di giro      D_d={# profondità  numero di stati  0:     1,  1:     12,  2:     114,  3:     1068,  4:     10011,  5:     93840,  6:     878880,  7:     8221632,  8:     76843595,  9:     717789576,  10:    6701836858,  11:    62549615248,  12:    583570100997,  13:    5442351625028,  14:    50729620202582,  15:    472495678811004,  16:    4393570406220123,  17:    40648181519827392,  18:    368071526203620348,  19:    3000000000000000000,  # approssimativo  20:    14000000000000000000, # approssimativo  21:    19000000000000000000, # approssimativo  22:    7000000000000000000,  # approssimativo  23:    24000000000000000,    # approssimativo  24:    150000,               # approssimativo  25:    36,  26:    3,  27:    0}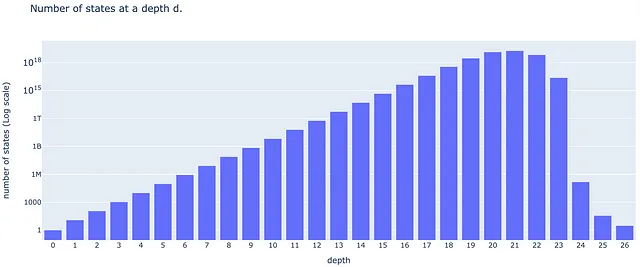

Alcune osservazioni su questa lista:

Prima di tutto, non ci sono stati a una profondità maggiore di 26 (il numero di Dio è 26 nella metrica dei quarti di giro). In secondo luogo, la lista riporta un numero approssimativo di stati per d compreso tra 19 e 24. Dovremo fare attenzione a questo in seguito. In terzo luogo, se facciamo un grafico a scala logaritmica, possiamo vedere una crescita lineare per la maggior parte delle profondità (tranne quelle vicine alla fine). Ciò significa che la popolazione D(d) degli stati cresce in modo esponenziale. Adattando la parte lineare del grafico logaritmico con una retta impariamo che tra d = 3 e d = 18 la popolazione degli stati cresce come

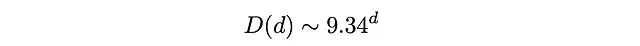
Alle profondità 3 < d < 18, in media, 9,34 delle 12 mosse ti faranno allontanare dallo stato risolto, mentre 2,66 ti faranno avvicinare.

Un processo di Markov sulle classi di profondità

Per trovare p(d|N) immaginiamo le classi di profondità come i siti di un processo di Markov. Permettimi di spiegarti:

Una classe di profondità d è l’insieme di tutti gli stati del cubo a una profondità d (numero minimo di mosse per arrivare allo stato risolto). Se scegliamo casualmente uno stato in una classe di profondità d e ruotiamo una faccia casuale con una mossa casuale, otterremo uno stato nella classe d + 1 con una probabilità p_d, oppure uno stato nella classe d – 1 con una probabilità q_d. Nella metrica dei quarti di rotazione non ci sono mosse che rimangono nella stessa classe.

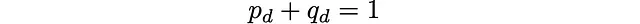
Ciò definisce un processo di Markov, in cui un sito particolare è un’intera classe di profondità. Nel nostro caso, solo le classi d contigue sono connesse da un salto. Per essere precisi, si tratta di una catena di Markov di nascita-morte a tempo discreto. Poiché il numero di siti è finito, la catena è anche irreducibile ed ergodica e esiste una distribuzione stazionaria unica.

Assumiamo probabilità uniformemente distribuite per la selezione delle mosse casuali in ogni istante. Ciò induce alcune probabilità di transizione p_d, q_d (da calcolare) tra le classi di profondità. Il numero di mosse casuali N è il tempo discreto del processo di Markov. Si tratta anche di un camminatore casuale unidimensionale: in ogni sito (numero di classe di profondità d), la probabilità di andare avanti è p_d, e la probabilità di tornare indietro è q_d. Questa catena unidimensionale è, in parole povere, la direzione “radiale” nel grafo di Rubik (organizzato nel layout di profondità-radiale).

La matrice di transizione

Ogni processo di Markov è codificato in una matrice di transizione M. L’elemento (i,j) di M è la probabilità di passare dal sito i al sito j. Nel nostro caso, solo le seguenti voci sono diverse da zero:

Qui p_0 = 1: dalla classe di profondità 0 (che contiene solo lo stato risolto) possiamo solo passare alla classe di profondità 1 (non esiste la classe -1). Inoltre, q_26 = 1: dalla classe di profondità 26 possiamo solo passare alla classe di profondità 25 (non esiste la classe 27). Per lo stesso motivo, non ci sono p_26 o q_0.

La distribuzione stazionaria

Abbiamo mappato l’azione di muovere casualmente il cubo in un walker casuale di classe di profondità unidimensionale che salta avanti e indietro con probabilità q_d e p_d. Cosa succede dopo una lunga camminata? O, quante volte il walker visita un sito particolare dopo una lunga camminata? Nella vita reale: con quale frequenza viene visitata una classe di profondità quando il cubo subisce svolte casuali?

A lungo termine, e indipendentemente dal punto di partenza, il tempo che il walker trascorre nella classe di profondità d è proporzionale alla popolazione D(d) di quella classe di profondità. Questo è il punto principale qui:

la lista di popolazione di profondità (normalizzata) D(d) dovrebbe essere interpretata come il vettore che rappresenta la distribuzione stazionaria del nostro processo di Markov di classe di profondità.

Matematicamente, D(d) è un autovettore sinistro di M

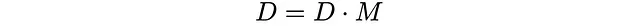
Questa equazione matriciale ci darà 26 equazioni lineari, dalle quali otterremo i p_i’ e i q_i.

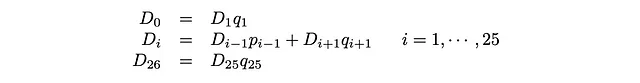
Tenendo conto che p_0 = q_26 = 1, possiamo riscrivere queste equazioni come

Queste sono note come equazioni di bilancio dettagliate: il flusso, definito come la popolazione stazionaria del sito moltiplicata per la probabilità di salto, è lo stesso in entrambe le direzioni. Le soluzioni sono:

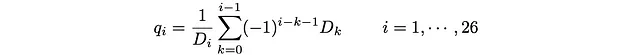
e p_i si ottiene utilizzando p_i + q_i = 1.

Alcune condizioni sulla popolazione di una classe di profondità

C’è qualcosa di interessante in queste soluzioni. Poiché q_i è una probabilità, dovremmo avere che

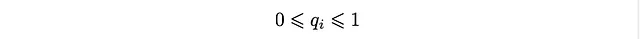
e ciò si traduce nella seguente condizione per la distribuzione D_k:

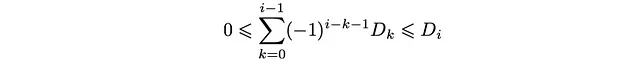
Questa è una sequenza di disuguaglianze che la popolazione di profondità D_k dovrebbe soddisfare. Esplicitamente, possono essere organizzate come:

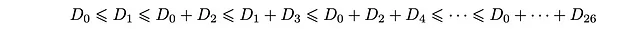
In particolare, le ultime due disuguaglianze sono

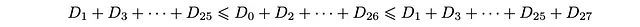
Poiché D_27 = 0, otteniamo che il limite inferiore e superiore sono uguali, quindi

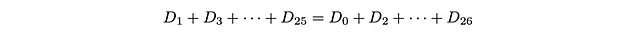
O:

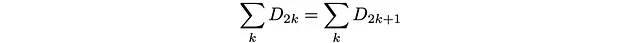
La somma della popolazione dei siti pari dovrebbe essere uguale alla somma della popolazione dei siti dispari!

Possiamo vedere questo come un equilibrio dettagliato tra siti pari e dispari: ogni mossa è sempre verso una classe di profondità diversa e contigua. Qualsiasi salto ti porterà dalla classe di profondità dispari (la classe di tutte le classi di profondità dispari) alla classe di profondità pari (la classe di tutte le classi di profondità pari). Quindi il salto dalla classe dispari a quella pari avviene con probabilità 1 (e viceversa). Essendo le probabilità entrambe uno in entrambe le direzioni, la loro popolazione dovrebbe essere uguale per equilibrio dettagliato.

Per lo stesso motivo, il processo di Markov raggiungerà una “distribuzione stazionaria” di periodo due che alterna tra siti pari e dispari dopo ogni mossa (tempo discreto N).

Un problema con i dati

La popolazione di profondità D_d riportata nella fonte dei dati che stiamo pianificando di utilizzare è approssimativa per d = 19,20,21,22,23,24. Quindi non c’è garanzia che soddisferà tutte queste condizioni (disuguaglianze). Non sorprenderti se otteniamo alcune probabilità q_i fuori dall’intervallo [0,1] (come nel caso attuale!). In particolare, se proviamo a verificare l’ultima condizione (l’uguaglianza della popolazione pari-dispari) è fuori di un grande numero! (aggiornamento: vedi nota alla fine)

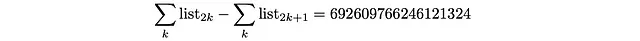
Una via d’uscita

La classe dispari sembra essere sottopopolata (questo è una conseguenza dell’approssimazione scelta dagli autori per riportare i dati). Per far funzionare le cose (ottenere probabilità nell’intervallo [0,1]), decidiamo di aggiungere il precedente grande numero alla popolazione della classe di profondità 21 (la classe dispari con la popolazione più grande, o quella che noterà meno questa aggiunta). Con questa correzione, tutte le probabilità ottenute sembrano essere corrette (il che significa che le disuguaglianze sono anche soddisfatte).

Le probabilità di salto sono:

p_i = {1., 0.916667, 0.903509, 0.903558, 0.903606, 0.903602, 0.90352, 0.903415, 0.903342, 0.903292, 0.903254, 0.903221, 0.903189, 0.903153, 0.903108, 0.903038, 0.902885, 0.902409, 0.900342, 0.889537, 0.818371, 0.367158, 0.00342857, 6.24863*1e-12, 0.00022, 0.0833333}# i da 0 a 25q_i = {0.0833333, 0.0964912, 0.0964419, 0.096394, 0.0963981, 0.0964796, 0.096585, 0.096658, 0.0967081, 0.0967456, 0.0967786, 0.0968113, 0.0968467, 0.0968917, 0.0969625, 0.0971149, 0.0975908, 0.0996581, 0.110463, 0.181629, 0.632842, 0.996571, 1., 0.99978, 0.916667, 1.}# i da 1 a 26

Notare che quasi tutti i primi p_i (fino a i = 21) sono vicini a 1. Queste sono le probabilità di allontanarsi dallo stato risolto. Le probabilità di avvicinarsi allo stato risolto (q_i) sono quasi 1 per i maggiore di 21. Questo mette in prospettiva perché è difficile risolvere il cubo: il camminatore casuale (o il movitore casuale del cubo) sarà “intrappolato per sempre” in una vicinanza della classe di profondità 21.

p(d|N)

Inserendo i valori numerici di p_i, q_i nella matrice di transizione M, il processo di Markov è completamente descritto. In particolare, se iniziamo dal sito 0 con probabilità uno, dopo N passi il camminatore casuale sarà nel sito d con probabilità:

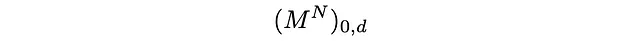
Questa è la probabilità che stavamo cercando:

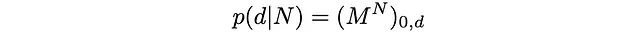
Numericalmente, apprendiamo che p(d|N) è diverso da zero solo se N e d hanno la stessa parità (cosa ben nota da alcuni studiosi del cubo di Rubik). Di seguito tracciamo alcune p(d|N) per diversi N:

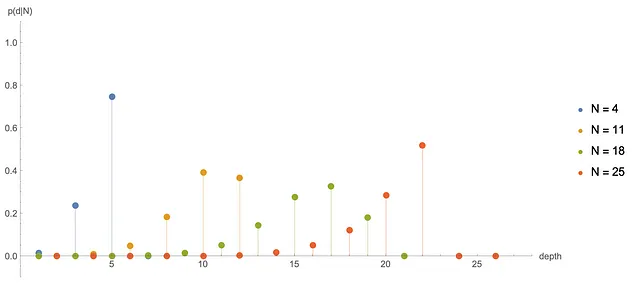
Osserviamo che dopo N = 31 o 32, p(d|N) è molto vicino alla distribuzione stazionaria D(d) (tranne che alterna tra siti pari e dispari). Questa è un’altra risposta alla domanda su quanti movimenti sono sufficienti per dire che abbiamo veramente mescolato il cubo.

Notiamo che abbiamo risolto un problema inverso. Abbiamo ottenuto le probabilità di transizione dalla distribuzione stazionaria. Questo non è possibile per un processo di Markov generale. In particolare, non è possibile trovare p(d|N), con il metodo descritto qui, per la metrica a mezza rotazione. La metrica a mezza rotazione è diversa perché possiamo rimanere nella stessa classe di profondità dopo una mossa (secondo la loro definizione di mosse). Questi salti di classe di profondità autoreferenziali introducono probabilità aggiuntive r_i nella diagonale della matrice di transizione e avremo più variabili che equazioni.

Commenti finali

Anche se il cubo di Rubik è un problema di 35 anni di CPU dal punto di vista computazionale, ci sono molti aspetti che possono essere descritti analiticamente o con modesti sforzi numerici. La probabilità che abbiamo calcolato qui è un esempio di ciò. Tutto ciò che abbiamo detto può essere facilmente generalizzato a cubi di Rubik più complessi. Una generalizzazione interessante è passare a dimensioni superiori: S = 4D, 5D, 6D, … cubo di Rubik dimensionale. Lo spazio degli stati in quei casi cresce in modo esponenziale con S. Quindi ci sono cubi per i quali la catena di Markov è lunga quanto vogliamo. In altre parole, abbiamo puzzle simili per i quali i numeri di Dio sono grandi quanto vogliamo (in parole povere, il numero di Dio è il logaritmo del numero di stati e il numero di stati aumenta con la dimensione S). In quei casi possiamo prendere certi limiti che spiegano alcuni aspetti del nostro caso 3D, come il seguente:

Nel limite di un grande numero di Dio G, la probabilità p(d|N) dovrebbe avvicinarsi alla distribuzione binomiale

Non è molto difficile capire perché potrebbe essere così. Se G è grande, la crescita esponenziale di D_d sarà molto stabile per la maggior parte dei d. Questa è una supposizione audace, ma non eccessivamente ardita:

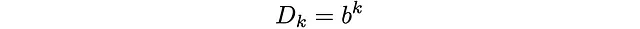
per k lontano da 0 e G. Come abbiamo detto, nel caso S = 3D b = 9.34. Per S più grandi, b dovrebbe aumentare (avere più facce aumenterà il fattore di ramificazione b). Questo si traduce nei seguenti valori delle probabilità:

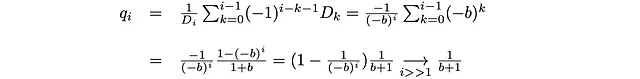
q_i si avvicina a un valore costante 1/(b+1) quando i è lontano dall’origine (i>>1) e dal numero di Dio (i<<G). p_i sarà anche costante in questo intervallo. Si può vedere che i valori di p_i e q_i calcolati qui per il caso 3D sono quasi costanti per i=3, …, 15, e che q_i è approssimativamente uguale a 1/(b+1) con b = 9.34. Per 0 << i << G avremo quindi un camminatore casuale unidimensionale con probabilità costanti di tornare indietro (q) e avanti (p). In questo caso la posizione del camminatore sarà descritta da una distribuzione simile a una distribuzione binomiale.

La probabilità che il camminatore casuale prenda k passi verso destra (tasso di successo p) e N-k passi verso sinistra (tasso di successo q) dopo N tentativi è Binomiale(k,N,p). La distanza percorsa dopo N passi sarà quindi

d = k – (N – k),

da cui otteniamo

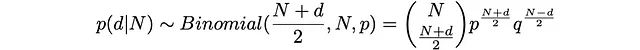
Da qui possiamo ottenere stime analitiche per il valore più probabile di d

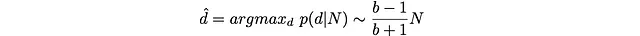
Questo è interessante: man mano che la dimensione S del cubo aumenta, il fattore di ramificazione b cresce e la profondità più probabile d si avvicina effettivamente a N.

Nota di aggiornamento. Dopo la pubblicazione di questa storia ho contattato Tomas Rokicki e Morley Davidson (due degli autori della dimostrazione del 2012 che il numero di Dio è 20 nella metrica a mezza rotazione) riguardo al loro D(d) riportato e alle probabilità negative che ho ottenuto usando esso. Mi hanno fornito dati più accurati, con limiti inferiori e superiori per la popolazione delle profondità d = 19, …, 24 . I loro dati sono pienamente compatibili con le disuguaglianze qui ottenute e con il fatto che la popolazione delle classi di profondità pari dovrebbe essere uguale a quella delle classi di profondità dispari (nella metrica a quarto di rotazione). Le probabilità calcolate qui hanno una correzione trascurabile quando si utilizzano questi nuovi dati.