Come risolvere i problemi di ottimizzazione utilizzando la programmazione lineare
Risolvere problemi di ottimizzazione con la programmazione lineare
Un’introduzione alla programmazione lineare e come risolverla utilizzando gli algoritmi grafici e simplex
Background
La programmazione lineare (LP) è una tecnica di ottimizzazione utilizzata per trovare la migliore soluzione, da una specifica funzione obiettivo, soggetta a determinati vincoli. Viene applicata in vari settori, dall’economia alla vendita online, quindi vale la pena conoscerla se si è un Data Scientist. La caratteristica chiave della LP è la parte lineare, il che significa che i vincoli e la funzione obiettivo sono formulati come una relazione lineare. In questo articolo, esamineremo un esempio di problema di LP e come può essere risolto utilizzando l’algoritmo simplex e il metodo grafico.
Metodo Grafico
Problema di Base
Inizieremo con il metodo grafico, poiché è il più semplice da capire e ci fornisce una vera intuizione sulla LP.
Supponiamo di gestire una piccola attività che vende frullati al prezzo di £3 e caffè al prezzo di £2, questi sono i nostri due variabili decisionali. A causa dei nostri vincoli sugli ingredienti, possiamo produrre solo 75 frullati e 100 caffè al giorno. Inoltre, disponiamo solo di 140 tazze al giorno per servire i nostri frullati e caffè. Ora, formuliamo questo come un problema di LP!
Formulazione
Se lasciamo che x sia i frullati e y sia il caffè, vogliamo massimizzare la seguente funzione obiettivo, c, come funzione delle variabili decisionali:
- 3 Modi Per Superare le Sfide della Qualità dei Dati in un Progetto di Analisi
- Nuove ricerche sull’IA dall’Università del Maryland indagano la sfida dello cramming per addestrare un modello linguistico su una singola GPU in un giorno
- Trasformare gli SMS con l’AI Un’esplorazione approfondita delle tecniche di elaborazione del linguaggio naturale
Soggetto ai seguenti vincoli:
Le variabili decisionali devono essere non negative.
Ora è il momento di rappresentare graficamente questi vincoli!
Rappresentazione Grafica
Essendo questo un problema bidimensionale, possiamo rappresentare graficamente i vincoli su un grafico cartesiano come linee rette (la parte lineare!):
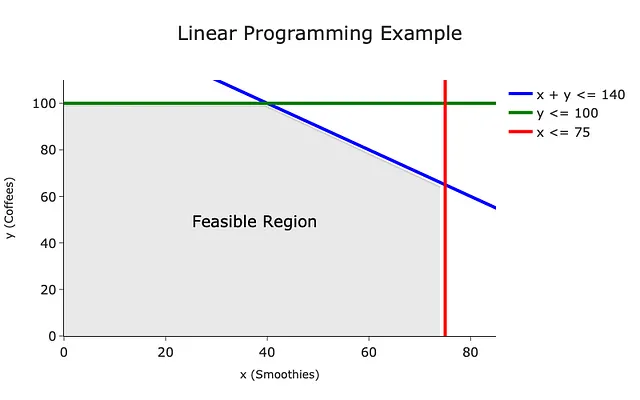
L’area grigia è nota come regione ammissibile, in cui qualsiasi soluzione è valida in quanto soddisfa il vincolo.

