Previsione di serie temporali probabilistiche con 🤗 Transformers
'Previsione serie temporali con 🤗 Transformers'
Introduzione
La previsione delle serie temporali è un problema scientifico e commerciale essenziale e, come tale, ha visto di recente molte innovazioni con l’uso di modelli basati sull’apprendimento profondo, oltre ai metodi classici. Una differenza importante tra i metodi classici come ARIMA e i nuovi metodi di apprendimento profondo è la seguente.
Previsione probabilistica
In genere, i metodi classici vengono adattati individualmente ad ogni serie temporale in un set di dati. Questi sono spesso definiti “metodi singoli” o “locali”. Tuttavia, quando si tratta di un grande numero di serie temporali per alcune applicazioni, è vantaggioso addestrare un modello “globale” su tutte le serie temporali disponibili, il che consente al modello di apprendere rappresentazioni latenti da molte fonti diverse.
Alcuni metodi classici sono a valore puntuale (cioè restituiscono un singolo valore per ogni passo temporale) e i modelli vengono addestrati minimizzando una perdita di tipo L2 o L1 rispetto ai dati di riferimento. Tuttavia, poiché le previsioni sono spesso utilizzate in una pipeline di decisioni nel mondo reale, anche con l’intervento umano, è molto più vantaggioso fornire le incertezze delle previsioni. Questo è anche chiamato “previsione probabilistica”, contrapposta alla “previsione puntuale”. Questo comporta la modellazione di una distribuzione probabilistica, da cui è possibile estrarre campioni.
- Utilizzo della diffusione stabile con Core ML su Apple Silicon
- Apprendimento profondo con le proteine
- Da GPT2 a Stable Diffusion Hugging Face arriva alla comunità di Elixir
Quindi, in breve, anziché addestrare modelli di previsione puntuale locali, speriamo di addestrare modelli probabilistici globali. L’apprendimento profondo è molto adatto a questo, poiché le reti neurali possono apprendere rappresentazioni da diverse serie temporali correlate e modellare l’incertezza dei dati.
Nel contesto probabilistico, è comune apprendere i futuri parametri di qualche distribuzione parametrica scelta, come la Gaussiana o la Student-T; oppure apprendere la funzione quantile condizionale; o utilizzare il framework della Conformal Prediction adattato all’ambiente delle serie temporali. La scelta del metodo non influisce sull’aspetto di modellazione e quindi può essere considerata tipicamente come un altro iperparametro. È sempre possibile trasformare un modello probabilistico in un modello di previsione puntuale, prendendo medie o mediane empiriche.
Il Time Series Transformer
In termini di modellazione dei dati delle serie temporali, che sono di natura sequenziale, come si può immaginare, i ricercatori hanno ideato modelli che utilizzano reti neurali ricorrenti (RNN) come LSTM o GRU, o reti convoluzionali (CNN), e più di recente metodi basati su Transformer, che si adattano naturalmente all’ambiente delle previsioni delle serie temporali.
In questo post del blog, sfrutteremo il Transformer “vanilla” (Vaswani et al., 2017) per il compito di previsione probabilistica univariata (cioè prevedendo individualmente la distribuzione a 1 dimensione di ciascuna serie temporale). Il Transformer Encoder-Decoder è una scelta naturale per la previsione poiché incorpora diverse aspettative induttive in modo elegante.
Inizialmente, l’uso di un’architettura Encoder-Decoder è utile durante l’inferenza, quando tipicamente per alcuni dati registrati desideriamo fare previsioni per alcuni passi futuri. Questo può essere paragonato al compito di generazione di testo in cui, dato un contesto, campioniamo il token successivo e lo passiamo al decoder (chiamato anche “generazione autoregressiva”). Allo stesso modo, qui possiamo anche, dato un certo tipo di distribuzione, estrarre campioni da essa per fornire previsioni fino all’orizzonte di previsione desiderato. Questo è noto come campionamento/generazione avido/a e c’è un ottimo post sul blog a riguardo nell’ambiente NLP.
In secondo luogo, un Transformer ci aiuta ad addestrare dati di serie temporali che potrebbero contenere migliaia di punti temporali. Potrebbe non essere fattibile inserire tutta la storia di una serie temporale contemporaneamente nel modello, a causa dei vincoli di tempo e memoria del meccanismo di attenzione. Pertanto, si può considerare una finestra di contesto appropriata e campionare questa finestra e la finestra di lunghezza di previsione successiva dai dati di addestramento quando si costruiscono i batch per la discesa del gradiente stocastico (SGD). La finestra di dimensione del contesto può essere passata all’encoder e la finestra di previsione a un decoder con maschera causale. Ciò significa che il decoder può guardare solo ai passi temporali precedenti quando apprende il valore successivo. Questo è equivalente a come si addestra un Transformer “vanilla” per la traduzione automatica, chiamato “teacher forcing”.
Un altro vantaggio dei Transformers rispetto alle altre architetture è che possiamo incorporare i valori mancanti (comuni nell’ambiente delle serie temporali) come una maschera aggiuntiva nell’encoder o nel decoder e addestrare comunque senza ricorrere al riempimento o all’imputazione. Questo è equivalente all’uso di attention_mask in modelli come BERT e GPT-2 nella libreria Transformers, per non includere i token di padding nel calcolo della matrice di attenzione.
Un inconveniente dell’architettura Transformer è il limite delle dimensioni del contesto e delle finestre di previsione a causa dei requisiti computazionali e di memoria quadratici del Transformer vanilla, vedi Tay et al., 2020. Inoltre, poiché il Transformer è un’architettura potente, potrebbe sovradattarsi o apprendere correlazioni spurie molto più facilmente rispetto ad altri metodi.
La libreria 🤗 Transformers include un modello Transformer vanilla per serie temporali probabilistiche, chiamato semplicemente Time Series Transformer. Nelle sezioni seguenti, mostreremo come addestrare un modello simile su un dataset personalizzato.
Configura l’ambiente
Prima di tutto, installiamo le librerie necessarie: 🤗 Transformers, 🤗 Datasets, 🤗 Evaluate, 🤗 Accelerate e GluonTS.
Come mostreremo, GluonTS verrà utilizzato per trasformare i dati e creare le caratteristiche, nonché per creare batch di addestramento, di convalida e di test appropriati.
!pip install -q transformers
!pip install -q datasets
!pip install -q evaluate
!pip install -q accelerate
!pip install -q gluonts ujsonCarica il dataset
In questo post del blog, utilizzeremo il dataset tourism_monthly, disponibile su Hugging Face Hub. Questo dataset contiene i volumi turistici mensili per 366 regioni in Australia.
Questo dataset fa parte del Monash Time Series Forecasting repository, una raccolta di dataset di serie temporali provenienti da diversi domini. Può essere considerato il benchmark GLUE per la previsione delle serie temporali.
from datasets import load_dataset
dataset = load_dataset("monash_tsf", "tourism_monthly")Come si può vedere, il dataset contiene 3 divisioni: addestramento, convalida e test.
dataset
>>> DatasetDict({
train: Dataset({
features: ['start', 'target', 'feat_static_cat', 'feat_dynamic_real', 'item_id'],
num_rows: 366
})
test: Dataset({
features: ['start', 'target', 'feat_static_cat', 'feat_dynamic_real', 'item_id'],
num_rows: 366
})
validation: Dataset({
features: ['start', 'target', 'feat_static_cat', 'feat_dynamic_real', 'item_id'],
num_rows: 366
})
})Ogni esempio contiene alcune chiavi, di cui start e target sono le più importanti. Diamo un’occhiata alla prima serie temporale nel dataset:
train_example = dataset['train'][0]
train_example.keys()
>>> dict_keys(['start', 'target', 'feat_static_cat', 'feat_dynamic_real', 'item_id'])Lo start indica semplicemente l’inizio della serie temporale (come una data e un’ora), e il target contiene i valori effettivi della serie temporale.
Lo start sarà utile per aggiungere caratteristiche legate al tempo ai valori della serie temporale, come input extra per il modello (ad esempio “mese dell’anno”). Dal momento che sappiamo che la frequenza dei dati è mensile, sappiamo ad esempio che il secondo valore ha il timestamp 1979-02-01, ecc.
print(train_example['start'])
print(train_example['target'])
>>> 1979-01-01 00:00:00
[1149.8699951171875, 1053.8001708984375, ..., 5772.876953125]Il set di convalida contiene gli stessi dati del set di addestramento, ma per un periodo di tempo più lungo pari a prediction_length. Questo ci permette di convalidare le previsioni del modello rispetto ai dati reali.
Il set di test è nuovamente un periodo di tempo più lungo di prediction_length rispetto al set di convalida (o un multiplo di prediction_length rispetto al set di addestramento per il test su finestre mobili multiple).
validation_example = dataset['validation'][0]
validation_example.keys()
>>> dict_keys(['start', 'target', 'feat_static_cat', 'feat_dynamic_real', 'item_id'])I valori iniziali sono esattamente gli stessi dell’esempio di addestramento corrispondente:
print(validation_example['start'])
print(validation_example['target'])
>>> 1979-01-01 00:00:00
[1149.8699951171875, 1053.8001708984375, ..., 5985.830078125]Tuttavia, questo esempio ha prediction_length=24 valori aggiuntivi rispetto all’esempio di addestramento. Verifichiamolo.
freq = "1M"
prediction_length = 24
assert len(train_example["target"]) + prediction_length == len(
validation_example["target"]
)Visualizziamolo:
import matplotlib.pyplot as plt
figure, axes = plt.subplots()
axes.plot(train_example["target"], color="blue")
axes.plot(validation_example["target"], color="red", alpha=0.5)
plt.show()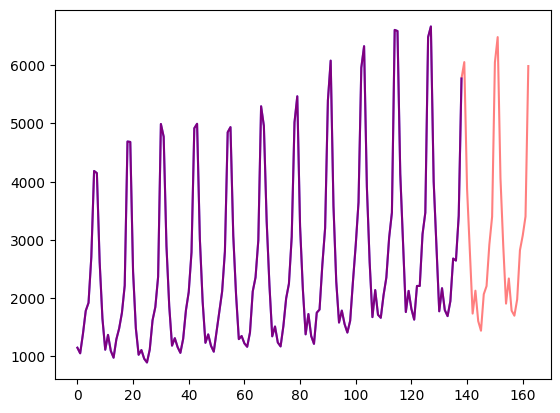
Suddividiamo i dati:
train_dataset = dataset["train"]
test_dataset = dataset["test"]Aggiorna start a pd.Period
La prima cosa che faremo è convertire la caratteristica start di ogni serie temporale in un indice pandas Period utilizzando la frequenza dei dati freq:
from functools import lru_cache
import pandas as pd
import numpy as np
@lru_cache(10_000)
def convert_to_pandas_period(date, freq):
return pd.Period(date, freq)
def transform_start_field(batch, freq):
batch["start"] = [convert_to_pandas_period(date, freq) for date in batch["start"]]
return batchOra utilizziamo la funzionalità set_transform di datasets per fare questo al volo:
from functools import partial
train_dataset.set_transform(partial(transform_start_field, freq=freq))
test_dataset.set_transform(partial(transform_start_field, freq=freq))Definire il Modello
Successivamente, istanziamo un modello. Il modello verrà addestrato da zero, quindi non utilizzeremo il metodo from_pretrained qui, ma inizializzeremo casualmente il modello da una config.
Specifichiamo un paio di parametri aggiuntivi per il modello:
prediction_length(nel nostro caso,24mesi): questo è l’orizzonte che il decoder del Transformer imparerà a predire;context_length: il modello imposteràcontext_length(input dell’encoder) uguale aprediction_length, se non viene specificatocontext_length;lagsper una data frequenza: questi specificano di quanto “guardiamo indietro”, da aggiungere come caratteristiche aggiuntive. ad esempio per una frequenzaGiornalierapotremmo considerare un’occhiata indietro di[1, 2, 7, 30, ...]o in altre parole guardiamo indietro di 1, 2, … giorni mentre per datiMinutipotremmo considerare[1, 30, 60, 60*24, ...]ecc.;- il numero di caratteristiche temporali: nel nostro caso, sarà
2poiché aggiungeremo le caratteristicheMeseDellAnnoedEta; - il numero di caratteristiche statiche categoriche: nel nostro caso, sarà solo
1poiché aggiungeremo una singola caratteristica “ID della serie temporale”; - la cardinalità: il numero di valori di ogni caratteristica statica categorica, come una lista che nel nostro caso sarà
[366]poiché abbiamo 366 diverse serie temporali - la dimensione dell’incorporamento: la dimensione dell’incorporamento per ogni caratteristica statica categorica, come una lista, ad esempio
[3]significa che il modello imparerà un vettore di incorporamento di dimensione3per ciascuna delle366serie temporali (regioni).
Utilizziamo i ritardi predefiniti forniti da GluonTS per la frequenza specificata (“mensile”):
from gluonts.time_feature import get_lags_for_frequency
lags_sequence = get_lags_for_frequency(freq)
print(lags_sequence)
>>> [1, 2, 3, 4, 5, 6, 7, 11, 12, 13, 23, 24, 25, 35, 36, 37]Questo significa che guarderemo indietro fino a 37 mesi per ogni passo temporale, come funzionalità aggiuntive.
Controlliamo anche le funzionalità temporali predefinite fornite da GluonTS:
from gluonts.time_feature import time_features_from_frequency_str
time_features = time_features_from_frequency_str(freq)
print(time_features)
>>> [<function month_of_year at 0x7fa496d0ca70>]In questo caso, c’è solo una singola funzionalità, vale a dire “mese dell’anno”. Ciò significa che per ogni passo temporale, aggiungeremo il mese come valore scalare (ad esempio, 1 nel caso in cui il timestamp sia “gennaio”, 2 nel caso in cui il timestamp sia “febbraio”, ecc.).
Ora abbiamo tutto per definire il modello:
from transformers import TimeSeriesTransformerConfig, TimeSeriesTransformerForPrediction
config = TimeSeriesTransformerConfig(
prediction_length=prediction_length,
# lunghezza del contesto:
context_length=prediction_length * 2,
# ritardi provenienti dall'helper in base alla frequenza:
lags_sequence=lags_sequence,
# aggiungeremo 2 funzionalità temporali ("mese dell'anno" e "età", vedere oltre):
num_time_features=len(time_features) + 1,
# abbiamo una singola funzionalità categorica statica, vale a dire l'ID delle serie temporali:
num_static_categorical_features=1,
# ha 366 valori possibili:
cardinality=[len(train_dataset)],
# il modello imparerà un embedding di dimensione 2 per ciascuno dei 366 valori possibili:
embedding_dimension=[2],
# parametri del transformer:
encoder_layers=4,
decoder_layers=4,
d_model=32,
)
model = TimeSeriesTransformerForPrediction(config)Nota che, simile ad altri modelli nella libreria 🤗 Transformers, TimeSeriesTransformerModel corrisponde al Transformer encoder-decoder senza alcuna testa in cima, e TimeSeriesTransformerForPrediction corrisponde a TimeSeriesTransformerModel con una testa di distribuzione in cima. Per impostazione predefinita, il modello utilizza una distribuzione Student-t (ma questo è configurabile):
model.config.distribution_output
>>> student_tQuesta è una differenza importante rispetto ai Transformers per NLP, dove la testa consiste tipicamente in una distribuzione categorica fissa implementata come un livello nn.Linear.
Definire le Trasformazioni
Successivamente, definiamo le trasformazioni per i dati, in particolare per la creazione delle funzionalità temporali (basate sul dataset o su funzionalità universali).
Di nuovo, utilizzeremo la libreria GluonTS per questo. Definiamo una Chain di trasformazioni (che è un po’ paragonabile a torchvision.transforms.Compose per le immagini). Ci consente di combinare diverse trasformazioni in un singolo pipeline.
from gluonts.time_feature import (
time_features_from_frequency_str,
TimeFeature,
get_lags_for_frequency,
)
from gluonts.dataset.field_names import FieldName
from gluonts.transform import (
AddAgeFeature,
AddObservedValuesIndicator,
AddTimeFeatures,
AsNumpyArray,
Chain,
ExpectedNumInstanceSampler,
InstanceSplitter,
RemoveFields,
SelectFields,
SetField,
TestSplitSampler,
Transformation,
ValidationSplitSampler,
VstackFeatures,
RenameFields,
)Le trasformazioni seguenti sono annotate con commenti per spiegare cosa fanno. A un livello elevato, itereremo sulle singole serie temporali del nostro dataset e aggiungeremo/rimuoveremo campi o funzionalità:
from transformers import PretrainedConfig
def create_transformation(freq: str, config: PretrainedConfig) -> Transformation:
remove_field_names = []
if config.num_static_real_features == 0:
remove_field_names.append(FieldName.FEAT_STATIC_REAL)
if config.num_dynamic_real_features == 0:
remove_field_names.append(FieldName.FEAT_DYNAMIC_REAL)
if config.num_static_categorical_features == 0:
remove_field_names.append(FieldName.FEAT_STATIC_CAT)
# un po' come torchvision.transforms.Compose
return Chain(
# passo 1: rimuovere campi statici/dinamici se non specificati
[RemoveFields(field_names=remove_field_names)]
# passo 2: convertire i dati in NumPy (potenzialmente non necessario)
+ (
[
AsNumpyArray(
field=FieldName.FEAT_STATIC_CAT,
expected_ndim=1,
dtype=int,
)
]
if config.num_static_categorical_features > 0
else []
)
+ (
[
AsNumpyArray(
field=FieldName.FEAT_STATIC_REAL,
expected_ndim=1,
)
]
if config.num_static_real_features > 0
else []
)
+ [
AsNumpyArray(
field=FieldName.TARGET,
# ci aspettiamo una dimensione aggiuntiva per il caso multivariato:
expected_ndim=1 if config.input_size == 1 else 2,
),
# passo 3: gestire i NaN riempiendo il target con zero
# e restituire la maschera (che è nei valori osservati)
# vero per i valori osservati, falso per i NaN
# il decoder utilizza questa maschera (non viene applicata alcuna perdita per i valori non osservati)
# vedere loss_weights all'interno del modello xxxForPrediction
AddObservedValuesIndicator(
target_field=FieldName.TARGET,
output_field=FieldName.OBSERVED_VALUES,
),
# passo 4: aggiungere funzionalità temporali in base alla frequenza del dataset
# mese dell'anno nel caso in cui freq="M"
# questi servono come codifiche posizionali
AddTimeFeatures(
start_field=FieldName.START,
target_field=FieldName.TARGET,
output_field=FieldName.FEAT_TIME,
time_features=time_features_from_frequency_str(freq),
pred_length=config.prediction_length,
),
# passo 5: aggiungere un'altra funzionalità temporale (solo un numero singolo)
# indica al modello in quale punto della sua vita si trova il valore della serie temporale,
# una sorta di contatore in esecuzione
AddAgeFeature(
target_field=FieldName.TARGET,
output_field=FieldName.FEAT_AGE,
pred_length=config.prediction_length,
log_scale=True,
),
# passo 6: impilare verticalmente tutte le funzionalità temporali nella chiave FEAT_TIME
VstackFeatures(
output_field=FieldName.FEAT_TIME,
input_fields=[FieldName.FEAT_TIME, FieldName.FEAT_AGE]
+ (
[FieldName.FEAT_DYNAMIC_REAL]
if config.num_dynamic_real_features > 0
else []
),
),
# passo 7: rinominare per corrispondere ai nomi di HuggingFace
RenameFields(
mapping={
FieldName.FEAT_STATIC_CAT: "static_categorical_features",
FieldName.FEAT_STATIC_REAL: "static_real_features",
FieldName.FEAT_TIME: "time_features",
FieldName.TARGET: "values",
FieldName.OBSERVED_VALUES: "observed_mask",
}
),
]
)Definisci InstanceSplitter
Per l’addestramento/validazione/test creiamo successivamente un InstanceSplitter che viene utilizzato per campionare finestre dal dataset (come, ricorda, non possiamo passare l’intera storia dei valori al Transformer a causa di vincoli di tempo e memoria).
L’instance splitter campiona finestre casuali di dimensione context_length e dimensione successiva prediction_length dai dati e aggiunge una chiave past_ o future_ a qualsiasi chiave temporale per le rispettive finestre. Ciò assicura che i values saranno divisi in chiavi past_values e future_values, che serviranno rispettivamente come input del codificatore e del decodificatore. La stessa cosa accade per qualsiasi chiave nell’argomento time_series_fields:
from gluonts.transform.sampler import InstanceSampler
from typing import Optional
def create_instance_splitter(
config: PretrainedConfig,
mode: str,
train_sampler: Optional[InstanceSampler] = None,
validation_sampler: Optional[InstanceSampler] = None,
) -> Transformation:
assert mode in ["train", "validation", "test"]
instance_sampler = {
"train": train_sampler
or ExpectedNumInstanceSampler(
num_instances=1.0, min_future=config.prediction_length
),
"validation": validation_sampler
or ValidationSplitSampler(min_future=config.prediction_length),
"test": TestSplitSampler(),
}[mode]
return InstanceSplitter(
target_field="values",
is_pad_field=FieldName.IS_PAD,
start_field=FieldName.START,
forecast_start_field=FieldName.FORECAST_START,
instance_sampler=instance_sampler,
past_length=config.context_length + max(config.lags_sequence),
future_length=config.prediction_length,
time_series_fields=["time_features", "observed_mask"],
)Crea DataLoaders
Successivamente, è il momento di creare i DataLoaders, che ci permettono di avere batch di coppie (input, output) – o in altre parole ( past_values , future_values ).
from typing import Iterable
import torch
from gluonts.itertools import Cached, Cyclic
from gluonts.dataset.loader import as_stacked_batches
def create_train_dataloader(
config: PretrainedConfig,
freq,
data,
batch_size: int,
num_batches_per_epoch: int,
shuffle_buffer_length: Optional[int] = None,
cache_data: bool = True,
**kwargs,
) -> Iterable:
PREDICTION_INPUT_NAMES = [
"past_time_features",
"past_values",
"past_observed_mask",
"future_time_features",
]
if config.num_static_categorical_features > 0:
PREDICTION_INPUT_NAMES.append("static_categorical_features")
if config.num_static_real_features > 0:
PREDICTION_INPUT_NAMES.append("static_real_features")
TRAINING_INPUT_NAMES = PREDICTION_INPUT_NAMES + [
"future_values",
"future_observed_mask",
]
transformation = create_transformation(freq, config)
transformed_data = transformation.apply(data, is_train=True)
if cache_data:
transformed_data = Cached(transformed_data)
# inizializziamo un'istanza di Training
instance_splitter = create_instance_splitter(config, "train")
# l'instance splitter campiona una finestra di
# lunghezza context + lags + prediction length (dai 366 possibili time series trasformati)
# casualmente all'interno della time series target e restituisce un iteratore.
stream = Cyclic(transformed_data).stream()
training_instances = instance_splitter.apply(
stream, is_train=True
)
return as_stacked_batches(
training_instances,
batch_size=batch_size,
shuffle_buffer_length=shuffle_buffer_length,
field_names=TRAINING_INPUT_NAMES,
output_type=torch.tensor,
num_batches_per_epoch=num_batches_per_epoch,
)
def create_test_dataloader(
config: PretrainedConfig,
freq,
data,
batch_size: int,
**kwargs,
):
PREDICTION_INPUT_NAMES = [
"past_time_features",
"past_values",
"past_observed_mask",
"future_time_features",
]
if config.num_static_categorical_features > 0:
PREDICTION_INPUT_NAMES.append("static_categorical_features")
if config.num_static_real_features > 0:
PREDICTION_INPUT_NAMES.append("static_real_features")
transformation = create_transformation(freq, config)
transformed_data = transformation.apply(data, is_train=False)
# creiamo un Test Instance splitter che campionerà l'ultima finestra
# di contesto vista solo per l'encoder durante l'addestramento.
instance_sampler = create_instance_splitter(config, "test")
# applichiamo le trasformazioni in modalità di test
testing_instances = instance_sampler.apply(transformed_data, is_train=False)
return as_stacked_batches(
testing_instances,
batch_size=batch_size,
output_type=torch.tensor,
field_names=PREDICTION_INPUT_NAMES,
)
train_dataloader = create_train_dataloader(
config=config,
freq=freq,
data=train_dataset,
batch_size=256,
num_batches_per_epoch=100,
)
test_dataloader = create_test_dataloader(
config=config,
freq=freq,
data=test_dataset,
batch_size=64,
)Controlliamo il primo batch:
batch = next(iter(train_dataloader))
for k, v in batch.items():
print(k, v.shape, v.type())
>>> past_time_features torch.Size([256, 85, 2]) torch.FloatTensor
past_values torch.Size([256, 85]) torch.FloatTensor
past_observed_mask torch.Size([256, 85]) torch.FloatTensor
future_time_features torch.Size([256, 24, 2]) torch.FloatTensor
static_categorical_features torch.Size([256, 1]) torch.LongTensor
future_values torch.Size([256, 24]) torch.FloatTensor
future_observed_mask torch.Size([256, 24]) torch.FloatTensorCome si può vedere, non forniamo input_ids e attention_mask all’encoder (come sarebbe il caso per i modelli NLP), ma piuttosto past_values, insieme a past_observed_mask, past_time_features e static_categorical_features.
Gli input del decoder consistono in future_values, future_observed_mask e future_time_features. I future_values possono essere considerati l’equivalente di decoder_input_ids in NLP.
Consultiamo la documentazione per una spiegazione dettagliata di ciascuno di essi.
Passaggio in Avanti
Eseguiamo un singolo passaggio in avanti con il batch appena creato:
# esegui il passaggio in avanti
outputs = model(
past_values=batch["past_values"],
past_time_features=batch["past_time_features"],
past_observed_mask=batch["past_observed_mask"],
static_categorical_features=batch["static_categorical_features"]
if config.num_static_categorical_features > 0
else None,
static_real_features=batch["static_real_features"]
if config.num_static_real_features > 0
else None,
future_values=batch["future_values"],
future_time_features=batch["future_time_features"],
future_observed_mask=batch["future_observed_mask"],
output_hidden_states=True,
)
print("Loss:", outputs.loss.item())
>>> Loss: 9.069628715515137Si noti che il modello restituisce una perdita. Questo è possibile perché il decoder sposta automaticamente i future_values di una posizione verso destra per avere le etichette. Ciò consente di calcolare una perdita tra i valori previsti e le etichette.
Inoltre, si noti che il decoder utilizza una maschera causale per non guardare nel futuro poiché i valori che deve prevedere sono nel tensore future_values.
Allenare il Modello
È ora di allenare il modello! Utilizzeremo un ciclo di allenamento standard di PyTorch.
Qui utilizzeremo la libreria 🤗 Accelerate, che posiziona automaticamente il modello, l’ottimizzatore e il dataloader sul dispositivo appropriato device.
from accelerate import Accelerator
from torch.optim import AdamW
accelerator = Accelerator()
device = accelerator.device
model.to(device)
optimizer = AdamW(model.parameters(), lr=6e-4, betas=(0.9, 0.95), weight_decay=1e-1)
model, optimizer, train_dataloader = accelerator.prepare(
model,
optimizer,
train_dataloader,
)
model.train()
for epoch in range(40):
for idx, batch in enumerate(train_dataloader):
optimizer.zero_grad()
outputs = model(
static_categorical_features=batch["static_categorical_features"].to(device)
if config.num_static_categorical_features > 0
else None,
static_real_features=batch["static_real_features"].to(device)
if config.num_static_real_features > 0
else None,
past_time_features=batch["past_time_features"].to(device),
past_values=batch["past_values"].to(device),
future_time_features=batch["future_time_features"].to(device),
future_values=batch["future_values"].to(device),
past_observed_mask=batch["past_observed_mask"].to(device),
future_observed_mask=batch["future_observed_mask"].to(device),
)
loss = outputs.loss
# Backpropagation
accelerator.backward(loss)
optimizer.step()
if idx % 100 == 0:
print(loss.item())Inferenza
All’atto dell’inferenza, è consigliato utilizzare il metodo generate() per la generazione autoregressiva, simile ai modelli di NLP.
La previsione coinvolge l’ottenimento dei dati dal campionatore dell’istanza di test, che campionerà la finestra di dimensione context_length degli ultimi valori da ciascuna serie temporale nel dataset e la passerà al modello. Nota che passiamo future_time_features, che sono noti in anticipo, al decoder.
Il modello campionerà in modo autoregressivo un certo numero di valori dalla distribuzione prevista e li passerà di nuovo al decoder per restituire le previsioni:
model.eval()
forecasts = []
for batch in test_dataloader:
outputs = model.generate(
static_categorical_features=batch["static_categorical_features"].to(device)
if config.num_static_categorical_features > 0
else None,
static_real_features=batch["static_real_features"].to(device)
if config.num_static_real_features > 0
else None,
past_time_features=batch["past_time_features"].to(device),
past_values=batch["past_values"].to(device),
future_time_features=batch["future_time_features"].to(device),
past_observed_mask=batch["past_observed_mask"].to(device),
)
forecasts.append(outputs.sequences.cpu().numpy())Il modello restituisce un tensore di forma ( batch_size , numero di campioni , lunghezza previsione ).
In questo caso, otteniamo 100 valori possibili per i prossimi 24 mesi (per ogni esempio nel batch di dimensione 64 ):
forecasts[0].shape
>>> (64, 100, 24)Li impileremo verticalmente, per ottenere previsioni per tutte le serie temporali nel dataset di test:
forecasts = np.vstack(forecasts)
print(forecasts.shape)
>>> (366, 100, 24)Possiamo valutare la previsione risultante rispetto ai valori fuori campione di riferimento presenti nel set di test. Utilizzeremo le metriche MASE e sMAPE che calcoliamo per ogni serie temporale nel dataset:
from evaluate import load
from gluonts.time_feature import get_seasonality
mase_metric = load("evaluate-metric/mase")
smape_metric = load("evaluate-metric/smape")
forecast_median = np.median(forecasts, 1)
mase_metrics = []
smape_metrics = []
for item_id, ts in enumerate(test_dataset):
training_data = ts["target"][:-prediction_length]
ground_truth = ts["target"][-prediction_length:]
mase = mase_metric.compute(
predictions=forecast_median[item_id],
references=np.array(ground_truth),
training=np.array(training_data),
periodicity=get_seasonality(freq))
mase_metrics.append(mase["mase"])
smape = smape_metric.compute(
predictions=forecast_median[item_id],
references=np.array(ground_truth),
)
smape_metrics.append(smape["smape"])
print(f"MASE: {np.mean(mase_metrics)}")
>>> MASE: 1.2564196892177717
print(f"sMAPE: {np.mean(smape_metrics)}")
>>> sMAPE: 0.1609541520852549Possiamo anche tracciare le metriche individuali di ogni serie temporale nel dataset e osservare che alcune serie temporali contribuiscono molto alla metrica di test finale:
plt.scatter(mase_metrics, smape_metrics, alpha=0.3)
plt.xlabel("MASE")
plt.ylabel("sMAPE")
plt.show()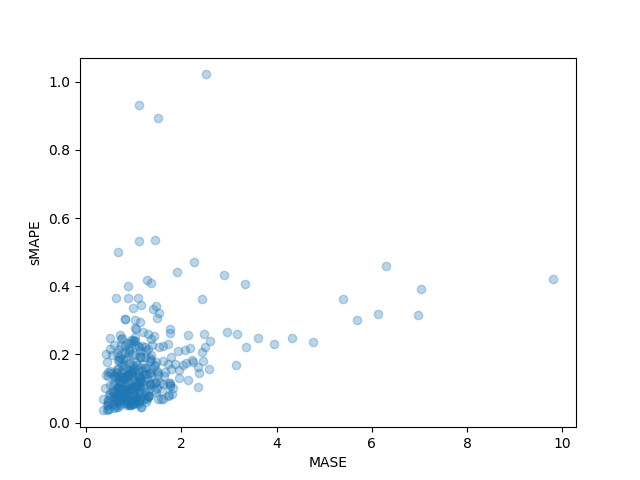
Per tracciare la previsione per qualsiasi serie temporale rispetto ai dati di test di riferimento, definiamo il seguente aiutante:
import matplotlib.dates as mdates
def plot(ts_index):
fig, ax = plt.subplots()
index = pd.period_range(
start=test_dataset[ts_index][FieldName.START],
periods=len(test_dataset[ts_index][FieldName.TARGET]),
freq=freq,
).to_timestamp()
# Major ticks every half year, minor ticks every month,
ax.xaxis.set_major_locator(mdates.MonthLocator(bymonth=(1, 7)))
ax.xaxis.set_minor_locator(mdates.MonthLocator())
ax.plot(
index[-2*prediction_length:],
test_dataset[ts_index]["target"][-2*prediction_length:],
label="reale",
)
plt.plot(
index[-prediction_length:],
np.median(forecasts[ts_index], axis=0),
label="mediana",
)
plt.fill_between(
index[-prediction_length:],
forecasts[ts_index].mean(0) - forecasts[ts_index].std(axis=0),
forecasts[ts_index].mean(0) + forecasts[ts_index].std(axis=0),
alpha=0.3,
interpolate=True,
label="+/- 1-std",
)
plt.legend()
plt.show()Ad esempio:
plot(334)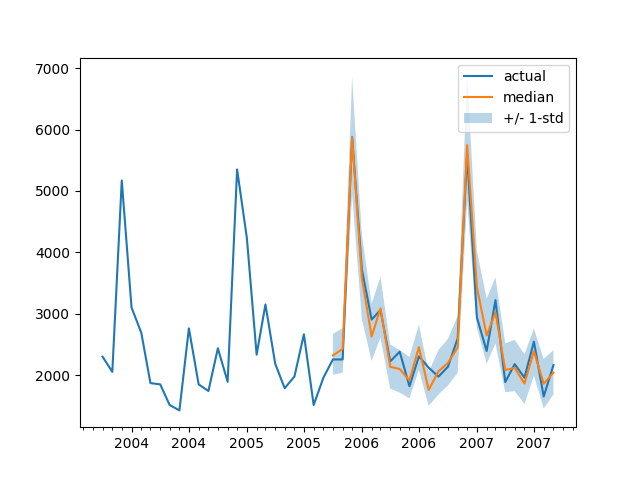
Come ci confrontiamo con altri modelli? Il Monash Time Series Repository ha una tabella di confronto delle metriche MASE sul set di test che possiamo aggiungere:
È importante notare che, con il nostro modello, superiamo tutti gli altri modelli riportati (vedi anche tabella 2 nel relativo articolo ) e non abbiamo effettuato alcuna ottimizzazione degli iperparametri. Abbiamo semplicemente addestrato il Transformer per 40 epoche.
Ovviamente, dobbiamo fare attenzione a dichiarare semplicemente risultati all’avanguardia sui time series con le reti neurali, poiché sembra che “XGBoost sia tutto ciò di cui hai bisogno” . Siamo solo molto curiosi di vedere fino a che punto le reti neurali possono portarci e se i Transformers saranno utili in questo campo. Questo particolare dataset sembra indicare che vale sicuramente la pena esplorarlo.
Prossimi passi
Invitiamo i lettori a provare il notebook con altri dataset di time series dal Hub e sostituire i parametri di frequenza e lunghezza di previsione appropriati. Per i tuoi dataset, sarà necessario convertirli alla convenzione utilizzata da GluonTS, che è spiegata chiaramente nella loro documentazione qui . Abbiamo anche preparato un notebook di esempio che mostra come convertire il tuo dataset nel formato dei dataset 🤗 qui .
Come sapranno i ricercatori di time series, c’è stato molto interesse nell’applicare modelli basati su Transformer al problema del time series. Il Transformer vanilla è solo uno dei molti modelli basati sull’attenzione, quindi è necessario aggiungere altri modelli alla libreria.
Al momento non c’è nulla che ci impedisca di modellare time series multivariate, tuttavia per questo sarebbe necessario istanziare il modello con una testa di distribuzione multivariata. Attualmente sono supportate solo distribuzioni indipendenti diagonali e altre distribuzioni multivariate verranno aggiunte. Restate sintonizzati per un futuro articolo che includerà un tutorial.
Un’altra cosa sulla roadmap è la classificazione delle time series. Ciò comporta l’aggiunta di un modello di time series con una testa di classificazione alla libreria, ad esempio per il rilevamento delle anomalie.
Il modello attuale assume la presenza di una data-ora insieme ai valori delle time series, il che potrebbe non essere il caso per ogni time series nel mondo reale. Ad esempio, guardate i dataset di neuroscienze come quello di WOODS . Pertanto, sarebbe necessario generalizzare il modello attuale per rendere alcune voci opzionali nell’intero processo.
Infine, il dominio NLP/Vision ha tratto enormi benefici da modelli pre-addestrati di grandi dimensioni , mentre questo non è il caso per quanto ne siamo a conoscenza nel dominio dei time series. I modelli basati su Transformer sembrano la scelta ovvia per perseguire questa linea di ricerca e non vediamo l’ora di vedere cosa scopriranno i ricercatori e gli esperti pratici!